 |
8.4. Коэффициент линейной корреляции Пирсона.
|
|
|
|
8. 4. Коэффициент линейной корреляции Пирсона.
Назначение и описание критерия
Коэффициент линейной корреляции Пирсона решает те же задачи, что и коэффициент ранговой корреляции Спирмена. Однако данный коэффициент рассчитан на шкалу интервалов или отношений, а не на шкалу порядка. Кроме этого, предполагается, что переменные X и Y должны быть распределены нормально.
При вычислении коэффициента не используется ранжирование, поэтому его расчёт является более простым, чем коэффициента ранговой корреляции.
В общем виде формула для подсчёта коэффициента корреляции Пирсона выглядит так:
rxy =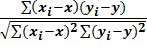 
, где 
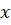и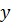 
- средние значения переменных X и Y. Может быть также использована модификация этой формулы:
rxy = 
, которая не предполагаетподсчёт средних значений переменных.
Критические значения коэффициента корреляции Пирсона ( Таблица 7 ) рассчитываются для величины k = n – 2 при 5≤ k ≤ 1000. Считается, что при достаточно большом n (если n> 40) распределение переменной должно быть близким к нормальному. Поэтому в этом случае можно вычислять коэффициент Пирсона rxy, а не коэффициент ранговой корреляции Спирмена rxy, таблица критических значений которого ( Таблица 8 ) предполагает n≤ 40.
Условия применения коэффициента линейной корреляции Пирсона
1) Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.
2) Распределения переменных X и Y должны быть близки к нормальному.
3) Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.
4) Таблицы уровней значимости для коэффициента корреляции ( Таблица 7 ) рассчитаны от n = 7 до n = 1000. Оценка уровня значимости осуществляется при числе степеней свободы k = n – 2.
|
|
|
Сравнение коэффициентов корреляции можно провести, решив одну и ту же задачу различными способами. В Примере 8. 1. задача решена с помощью коэффициента ранговой корреляции Спирмена. Пример 8. 3. – это решение той же самой задачи с помощью коэффициента линейной корреляции Пирсона.
Пример 8. 3. 20 школьникам были розданы тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Решение: Введём переменные: X – среднее время решения наглядно-образных, Y – среднее время решения вербальных тестов. Данные переменные измерены в шкале отношений. (Переменные распределены нормально. Этот факт нуждается в дополнительной проверке, которая здесь опускается). Ответ на вопрос получим с помощью критерия линейной корреляции Пирсона. Исходные данные представлены в виде таблицы.
| № испытуемых п/п | X Среднее время решения наглядно-образных заданий | Y Среднее время решения вербальных заданий | X 
| X2 | Y2 |
| Сумма | 20. 089 | 27. 873 | 16. 000 |
Формулировка гипотез:
Н0: Корреляция между средним временем решения наглядно-образных и вербальных заданий не отличается от нуля.
Н1: Корреляция между средним временем решения наглядно-образных и вербальных заданий достоверно отличается от нуля.
Алгоритм подсчёта коэффициента корреляции Пирсона:
1) Заполняем все столбцы таблицы, рассчитать суммы.
|
|
|
2) Рассчитываем эмпирическую величину коэффициента корреляции по формуле:
rxy = 
=
= 
= 0, 669
3) Находим критические значения коэффициента корреляции по Таблице 7. Число степеней свободы: k = n – 2 = 20 – 2 = 18.
rкр = 0, 44 (Р≤ 0, 05); rкр = 0, 56 (Р≤ 0, 01).
4) Строим ось значимости. rxy попадает в зону значимости.
| 0, 05 0, 01 |
| Зона значимости |
| 0, 44 0, 56 0, 669 |
5) Вывод. Отвергается Н0 и принимается Н1. Связь между временем решения наглядно-образных и вербальных задач статистически значима на 1% уровне и положительна. Полученная прямо пропорциональная зависимость говорит о том, что чем выше среднее время решения наглядно-образных задач, тем выше среднее время решения вербальных задач и наоборот.
Таким образом, подтвердился результат решения данной задачи методом ранговой корреляции Спирмена.
|
|
|
