 |
8.3. Ранговый коэффициент линейной корреляции Спирмена.
|
|
|
|
8. 3. Ранговый коэффициент линейной корреляции Спирмена.
Назначение и описание метода
Метод ранговой корреляции Спирмена позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков.
Для подсчёта ранговой корреляции необходимо располагать двумя рядами значений (X и Y), которые могут быть проранжированы. Такими рядами могут быть:
1) два признака, измеренные в одной и той же группе испытуемых;
2) две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (например, личностные профили по 16-факторному опроснику Кеттела, иерархии ценностей по методике Рокича, последовательности предпочтений в выборе из нескольких альтернатив и т. д. );
3) две групповые иерархии признаков;
4) индивидуальная и групповая иерархии признаков.
Вначале показатели ранжируются отдельно по каждому из признаков. Как правило, меньшему значению признака начисляется меньший ранг.
Ранговый коэффициент линейной корреляции Спирмена вычисляется по формуле:
rxy = 1 – 
, где n – количество ранжируемых признаков (показателей, испытуемых),
D – разность между рангами по двум переменным для каждого испытуемого,
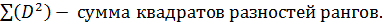
Формулировка статистических гипотез:
Н0: Корреляция между переменными (иерархиями) X и Y не отличается от нуля.
Н1: Корреляция между переменными (иерархиями) X и Y достоверно отличается от нуля.
Условия применения коэффициента ранговой корреляции Спирмена
1. Сравниваемые переменные должны быть получены в порядковой (ранговой) шкале, но могут быть измерены также в шкале интервалов и отношений. В последнем случае необходимо проранжировать показатели и перейти к порядковой шкале.
|
|
|
2. Характер распределения коррелируемых величин не имеет значения.
3. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
4. Таблицы для определения критических значений коэффициента корреляции Спирмена ( Таблица 8 ) рассчитаны на n от 5 до 40. Нахождение критических значений осуществляется при k = n.
Алгоритм подсчёта коэффициента ранговой корреляции Спирмена ρ xy
1) Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные X и Y.
2) Проранжировать значения переменной X, начисляя ранг 1 наименьшему значению. Занести ранги в первый столбец таблицы по порядку номеров испытуемых или признаков.
3) Проранжировать значения переменной Y в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.
4) Подсчитать разности D между рангами X и Y по каждой строке таблицы и занести в третий столбец таблицы.
5) Возвести каждую разность в квадрат: D2. Эти значения занести в четвёртый столбец таблицы. Подсчитать сумму квадратов 
).
6) Рассчитать коэффициент ранговой корреляции ρ xy по формуле
rxy = 1 –
7) Определить критические значения коэффициента ранговой корреляции по Таблице 8.
8) Построить ось значимости. Определить зону попадания rxy.
9) Сформулировать выводы.
Пример 8. 1. 20 школьникам были розданы тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Решение: Введём переменные: X – среднее время решения наглядно-образных, Y – среднее время решения вербальных тестов. Ответ на вопрос получим с помощью критерия ранговой корреляции Спирмена. Исходные данные представлены в виде таблицы (1, 2 и 3 столбцы).
|
|
|
| № испытуемых п/п | X Среднее время решения наглядно-образных заданий | Y Среднее время решения вербальных заданий | RX | RY | D | D2 |
| -5 | ||||||
| 5, 5 | 4, 5 | 20, 25 | ||||
| 7, 5 | 1, 5 | 2, 25 | ||||
| 13, 5 | 3, 5 | 12, 25 | ||||
| -9 | ||||||
| -6 | ||||||
| 11, 5 | 3, 5 | 12, 25 | ||||
| 11, 5 | 5, 5 | 30, 25 | ||||
| 17, 5 | -0, 5 | 0, 25 | ||||
| 13, 5 | -3, 5 | 12, 25 | ||||
| 17, 5 | -4, 5 | 20, 25 | ||||
| 14, 5 | 19, 5 | -5 | ||||
| 5, 5 | -3, 5 | 12, 25 | ||||
| 19, 5 | 0, 5 | 0, 25 | ||||
| 14, 5 | 10, 5 | |||||
| 7, 5 | 3, 5 | 12, 25 | ||||
| 10, 5 | 8, 5 | 72, 25 | ||||
| Сумма |
Формулировка гипотез:
Н0: Корреляция между средним временем решения наглядно-образных и вербальных заданий не отличается от нуля.
Н1: Корреляция между средним временем решения наглядно-образных и вербальных заданий достоверно отличается от нуля.
Алгоритм подсчёта коэффициента ранговой корреляции Спирмена:
1) Переменная X – среднее время решения наглядно-образных заданий. Её значения вносятся во второй столбец таблицы. Переменная Y – среднее время решения вербальных заданий. Значения вносятся в третий столбец таблицы.
2) Ранжируем значения переменной X. Ранги RX вносятся в четвёртый столбец таблицы. Находим сумму рангов (210). Проверяем правильность ранжирования: N(N+1)\ 2 = 20·21\ 2 = 210. Ранжирование проведено верно, так как суммы рангов совпали.
3) Ранжируем значения переменной Y. Ранги RY вносятся в пятый столбец таблицы. Находим сумму рангов (210). Ранжирование проведено верно, так как суммы рангов совпали.
4) Подсчитываем разности D между рангами X и Y по каждой строке таблицы и заносим в шестой столбец таблицы.
5) Возводим каждую разность в квадрат: D2. Эти значения заносим в седьмой столбец таблицы. Подсчитываем сумму квадратов ) = 392.
6) Рассчитываем коэффициент ранговой корреляции ρ xy по формуле
rxy 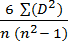= 1 – 
= 1 – 
= 1 – 0, 295 = 0, 705
7) Определяем критические значения коэффициента ранговой корреляции для n = 20 по Таблице 8:
rкр = 0, 45 (Р≤ 0, 05); rкр = 0, 57 (Р≤ 0, 01).
8) Построим ось значимости. rxy попало в зону значимости.
|
|
|
| 0, 05 0, 01 |
| Зона значимости |
| 0, 45 0, 57 0, 705 |
9) Формулируем выводы. Гипотеза Н0 отклоняется и принимается гипотеза Н1: корреляция между средним временем решения наглядно-образных и вербальных заданий достоверно отличается от нуля. Между временем решения этих задач существует высокая значимая положительная корреляция. Полученная прямо пропорциональная зависимость говорит о том, что чем выше среднее время решения наглядно-образных задач, тем выше среднее время решения вербальных задач и наоборот.
Пример 8. 2. Психолога интересует вопрос: в какой степени совпадают оценки супругов к личностным качествам, имеющим определяющее значение для семейного благополучия.
Решение: Супругов просят проранжировать 7 личностных черт. Данные представлены в таблице. Для решения задачи используется коэффициент ранговой корреляции Спирмена.
| Качества личности | Муж (ранги) | Жена (ранги) | D |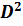 
|
| Ответственность | ||||
| Общительность | -4 | |||
| Сдержанность | -4 | |||
| Выносливость | -4 | |||
| Жизнерадостность | ||||
| Терпеливость | ||||
| Решительность | ||||
| Сумма |
Формулировка гипотез:
Н0: Корреляция между оценками супругов личностных качеств, имеющих определяющее значение для семейного благополучия, не отличается от нуля.
Н1: Корреляция между оценками супругов личностных качеств, имеющих определяющее значение для семейного благополучия, достоверно отличается от нуля.
Алгоритм подсчёта коэффициента ранговой корреляции Спирмена:
1) Заполнить таблицу, включая все столбцы и строки.
2) Рассчитать эмпирическое значение коэффициента ранговой корреляции Спирмена.
rxy 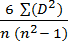= 1 – =1 –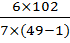 
= - 0, 82
3) Найти критические значения коэффициента ранговой корреляции Спирмена по Таблице 8 для n = 7.
rкр = 0, 78 (Р≤ 0, 05); rкр = 0, 94 (Р≤ 0, 01).
4) Построим ось значимости. rxy попало в зону неопределённости.
| 0, 05 0, 01 |
| 0, 78 0, 82 0, 94 |
| Зона неопределённости |
|
|
|
5) Формулируем вывод. Гипотеза Н0 отклоняется и принимается гипотеза Н1: корреляция между оценками супругов к личностным качествам, имеющим определяющее значение для семейного благополучия, достоверно отличается от нуля. Между оценками существует значимая отрицательная корреляция, что свидетельствует о достаточной степени рассогласованности (антагонизма) мнений супругов по данному вопросу.
|
|
|
