 |
2.Сравнение двух экспериментальных выборок.
|
|
|
|
2. Сравнение двух экспериментальных выборок.
Пример 7. 2. В двух школах района выяснялась успешность знания алгебры учащимися десятых классов. Для этого в обеих школах были случайным образом отобраны 50 учащихся и с ними проведены контрольные работы. Проверялось предположение о том, что существенной разницы в уровне знаний учащимися алгебры в двух школах не существует.
Решение: Результаты контрольных работ представлены в таблице.
| Школы |
Оценки |
Суммы | |||
| Школа 1 | О11 = 3 | О12= 19 | О13 = 18 | О14 = 10 | |
| Школа 2 | О22 = 9 | О22 = 24 | О23 = 12 | О24 = 5 | |
| Суммы | О11+О21=12 | О12+О22=43 | О13+О23=30 | О14+О24=15 | |
Формулировка гипотез:
Н0: Существенной разницы в уровне знаний учащимися алгебры в двух школах не существует.
Н1: Существенная разница в уровне знаний учащимися алгебры в двух школах существует.
Алгоритм подсчёта критерия c2:
1) Заполняется восьмипольная таблица.
2) Подсчёт эмпирического значения проводится по формуле:
c2эмп = 
c2эмп =  = 6, 45
= 6, 45
3) Число степеней свободы: n= (4 – 1)·(2 – 1) = 3
4) По Таблице 5 находятся критические значения:
c2кр 1 = 7, 815 (Р≤ 0, 05); c2кр 2 = 11, 345 (Р≤ 0, 01).
5) Строится ось значимости. c2эмп попадает в зону незначимости.
| Зона незначимости |
| 6, 45 7, 815 11, 345 |
| 0, 05 0, 01 |
6) Вывод: принимается гипотеза Н0 о сходстве. Уровни знаний учащимися алгебры в двух разных школах статистически значимо не отличаются.
7. 3. Критерий Фишера – φ.
Назначение и описание критерия
Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект.
|
|
|
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол j, а меньшей доле – меньший угол, но соотношения здесь не линейные:
j = 2·arcsin  , где Р – процентная доля, выраженная в долях единицы.
, где Р – процентная доля, выраженная в долях единицы.
Формулировка гипотез:
Н0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.
Н1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.
Условия применения критерия Фишера - j
1) Ни одна из сопоставляемых долей не должна быть равной нулю. В противном случае результат может оказаться неоправданно завышенным.
2) Верхний предел в критерии j отсутствует – выборки могут быть сколь угодно большими.
3) Нижний предел – 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:
а) если в одной из выборок всего 2 наблюдения, то во второй должно быть не менее 30;
б) если в одной всего 3 наблюдения, то во второй должно быть не меньше 7;
в) если в одной всего 4 наблюдения, то во второй – не менее 5;
г) при n1, n2 ≥ 5 возможны любые сопоставления.
Других ограничений у критерия j нет.
Алгоритм подсчёта критерия Фишера - j
1) Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта».
2) Подсчитать количества испытуемых, у которых «есть эффект» в первой и во второй группах.
3) Определить процентные доли испытуемых, у которых «есть эффект», путём отнесения их количества к общему числу испытуемых в данной группе (выборке).
|
|
|
4) Проверить, не равняется ли одна из сопоставляемых процентных долей нулю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно, отказаться от данного критерия и использовать критерий c2.
5) Определить по Таблице 6 величины углов j для каждой из сопоставленных процентных долей.
6) Подсчитать эмпирическое значение j по формуле:
jэмп = (j1 - j2) · 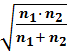
где j1 – угол, соответствующий большей процентной доле;
j2 – угол, соответствующий меньшей процентной доле;
n1 – количество наблюдений в выборке 1;
n2 – количество наблюдений в выборке 2.
7) Сопоставить полученное значение jэмп с критическими значениями, которые постоянны:
jкр = 1, 64 (Р≤ 0, 05); jкр = 2, 31 (Р≤ 0, 01),
построив ось значимости.
8) Сформулировать выводы.
Пример 7. 3. Психолог провёл эксперимент, в котором выяснилось, что из 23 учащихся математической спецшколы 15 справились с заданием, а из 28 обычной школы с тем же заданием справились 11 человек. Можно ли считать, что различия в успешности решения заданий учащимися спецшколы и обычной школы достоверны?
Решение: с помощью критерия Фишера φ.
Формулировка гипотез:
Н0: Различий в успешности решения заданий учащимися спецшколы и обычной школы нет.
Н1: Различия в успешности решения заданий учащимися спецшколы и обычной школы существуют.
Алгоритм подсчёта критерия j:
1) Критерием для разделения групп является успешность в выполнении задания.
2) Показатели успешности выполнения заданий необходимо перевести в проценты:
 ·100% = 65, 2% для спецшколы;
·100% = 65, 2% для спецшколы;
 ·100% = 39, 3% для обычной школы.
·100% = 39, 3% для обычной школы.
3) По Таблице 6 находим величины φ 1 и φ 2, соответствующие процентным долям в каждой группе.
Для 65, 2% φ 1= 1, 880, а для 39, 3% φ 2 = 1, 355.
4) Подсчитываем эмпирическое значение φ эмп по формуле:
jэмп = (j1 - j2) · 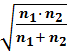
где n1 – количество наблюдений в выборке 1;
n2 - количество наблюдений в выборке 2.
В нашем случае φ эмп = (1, 880 – 1, 355)  = 1, 86
= 1, 86
5) Критические значения имеют фиксированную величину и составляют:
jкр = 1, 64 (Р≤ 0, 05); jкр = 2, 31 (Р≤ 0, 01).
6) Строим ось значимости. φ эмп попало в зону неопределённости.
| 0, 05 Зона неопределённости 0, 01 |
| 1, 64 1, 86 2, 31 |
|
|
|
7) Вывод. На 5% уровне значимости можно говорить о различии между успешностью в решении заданий учениками сравниваемых школ, а на уровне в 1% этого утверждать нельзя. На основании сравнения процентных долей можно утверждать, что учащиеся спецшколы успешнее справились с заданием, чем учащиеся обычной школы.
|
|
|


