 |
7.2. Критерий хи-квадрат. Назначение и описание критерия. Условия применения критерия хи-квадрат. Решение задач. 1. Сравнение двух экспериментальных распределений.
|
|
|
|
7. 2. Критерий хи-квадрат.
Назначение и описание критерия
Критерий построен так, что при полном совпадении распределений величина c2эмп = 0, и чем больше расхождение между сопоставляемыми распределениями, тем больше величина эмпирического значения хи-квадрат.
Основная расчётная формула критерия хи-квадрат выглядит так:
c2эмп = 
,
где fэ- эмпирическая частота,
fm – теоретическая частота,
k – количество разрядов признака.
Расчётная формула критерия хи-квадрат для сравнения двух эмпирических распределений в зависимости от вида представленных данных может иметь вид:
c2эмп = 
где N и M – соответственно числа элементов в первой и во второй выборке. Эти числа могут совпадать, а могут быть и различными.
Для расчётов в конкретных случаях используются различные модификации основной формулы, что позволяет облегчить процесс вычисления.
Для критерия хи-квадрат оценка уровней значимости определяется по Таблице 5 по числу степеней свободы n, которое в большинстве случаев вычисляется по формуле: n= k-1, где k каждый раз определяется по выборочным данным и представляет собой число элементов в выборке. Если при расчёте критерия используется таблица экспериментальных данных, то величина n рассчитывается следующим образом:
n = (k-1)·(c-1),
где k- число строк, а c – число столбцов таблицы.
Условия применения критерия хи-квадрат
1) Объём выборки должен быть достаточно большим: n≥ 20. При n< 20 критерий c2 даёт весьма приближённые значения. Точность критерия повышается при больших n.
2) Измерение может быть проведено в любой шкале.
3) Выборки должны быть случайными и независимыми.
4) Теоретическая частота для каждого выборочного интервала не должна быть меньше 5.
|
|
|
5) Сумма наблюдений по всем интервалам должна быть равна общему количеству наблюдений.
6) Таблица критических значений критерия c2 рассчитана для числа степеней свободы n, которое каждый раз рассчитывается по определённым правилам.
Решение задач
1. Сравнение двух экспериментальных распределений.
Исходные данные двух эмпирических распределений для сравнения между собой могут быть представлены разными способами. Наиболее простой из этих способов – так называемая «четырёхпольная таблица». Она используется в том случае, когда в первой выборке имеются два значения (числа) и во второй выборке также 2 значения (числа). Критерий позволяет также сравнивать между собой 3, 4 и больше число эмпирических величин.
Пример 7. 1. Одинаков ли уровень подготовленности учащихся в двух школах, если в первой школе из 100 человек поступили в вуз 82 человека, а во второй школе из 87 человек поступили в вуз 44?
Решение: Условия задачи можно представить в виде четырёхпольной таблицы (Таблица 1), в которой ячейки обозначаются как А, В, С и Д.
Таблица 1.
| 1 школа | 2 школа | |
| Число поступивших в вуз | А 82 | В 44 |
| Число не поступивших в вуз | С 18 | Д 43 |
| Сумма |
Формулировка гипотез:
Н0: Уровень подготовки учащихся в двух школах не является различным.
Н1: Уровень подготовки учащихся в двух школах является различным.
Алгоритм подсчёта критерия c2:
1) Имеется 4 эмпирические частоты. Необходимо для каждой из них найти соответствующие «теоретические» частоты. Они вычисляются различными способами в зависимости от типа задачи. В нашем случае: подсчитывается величина Р (доля признака, или частота признака). В нашем случае признак – то, что выпускники не поступили в вуз.
Р =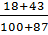 
= 0, 33
2) Величина Р позволяет рассчитать «теоретические» частоты для третьей строчки таблицы. Они показывают, сколько учащихся из 1 и 2 школ не должны были поступить в вуз:
|
|
|
fm1 = 0, 33. 100 = 33; fm2 = 0, 33. 87 = 28, 71
fm3 = 100 - 33 = 67; fm4 = 87 – 28, 71 = 58, 29
3) Составим новую таблицу с «теоретическими» частотами (Таблица 2):
Таблица 2.
| 1 школа | 2 школа | |
| Число учащихся, которые должны были бы поступить в вуз | А fm3 = 67 | В fm4 = 58, 29 |
| Число учащихся, которые не должны были бы поступить в вуз | С fm1 = 33 | Д fm2 = 28, 71 |
| Сумма |
4) Подсчитывается величина критерия хи-квадрат эмпирическая подсчитывается по основной формуле. Для этого из величин, представленных в ячейках Таблицы 1, вычитаются соответствующие величины, представленные в ячейках Таблицы 2.
c2эмп = 
= 20, 79
5) Подсчитаем число степеней свободы:
n = (k-1)(c-1) = (2 – 1) (2 – 1) = 1, так как в таблице 2 строки и 2 столбца.
6) По Таблице 5 находим:
c2кр1 = 3, 841 (Р≤ 0, 05); c2кр 2 = 6, 635 (Р≤ 0, 01).
7) Строим ось значимости. c2эмп попадает в зону значимости.
| Зона значимости |
| 0, 05 0, 01 |
| 3, 841 6, 635 20, 79 |
8) Вывод. Следует принять гипотезу о наличии различий между двумя эмпирическими распределениями. Таким образом, уровень подготовки учащихся в двух школах оказался различным. На основании эмпирических данных теперь можно утверждать, что уровень подготовленности учащихся в первой школе существенно выше, чем во второй.
|
|
|
