 |
Вопросы для обсуждения. ТЕМА №9. Параметрические критерии различий. 9.1. Понятие о параметрических критериях. 9.2. t-критерий Стьюдента.
|
|
|
|
Вопросы для обсуждения
1. Что такое «корреляционня связь»? В чём отличие функциональной и корреляционной зависимости?
2. Какая корреляционная связь называется линейной, положительной, отрицательной, нулевой?
3. Каковы основные коэффициенты корреляции и основание для их классификации? Какова область значений коэффициента корреляции?
4. Какова общая классификация корреляционных связей?
5. Какова частная классификация корреляционных связей?
6. Какова корреляционная связь, если коэффициент корреляции:
а) r = 0, 55;
б) r = 0, 05;
в) r = 0, 55 (Р ≤ 0, 05);
г) r = 0, 75 (Р ≤ 0, 01);
д) r = 0, 75 (Р ≤ 0, 001).
7. Каково назначение рангового коэффициента корреляции Спирмена? Каков смысл данного метода? Какова формулировка гипотез?
8. Каковы условия применения рангового коэффициента корреляции Спирмена?
9. Каков алгоритм подсчёта рангового коэффициента корреляции Спирмена?
10. Каковы основные типы задач, решаемые методом ранговой корреляции?
11. Каково назначение коэффициента линейной корреляции Пирсона? Каков смысл данного метода? Какова формулировка гипотез?
12. Каковы условия применения коэффициента линейной корреляции Пирсона?
13. Каков алгоритм подсчёта коэффициента линейной корреляции Пирсона? 14. Проведите сопоставительный анализ коэффициентов корреляции Спирмена и Пирсона.
15. Вы хотите выявить корреляционную связь между уровнем самоактуализации и уровнем профессионального выгорания педагогов школы. В вашей выборке 35 педагогов. Какой статистический метод вы примените?
16. Что необходимо изменить в условиях вашего исследования, чтобы можно было применить другой метод выявления корреляционной связи?
17. Вы выявили, что существует корреляционная связь между уровнем развития абстрактного мышления и возрастом учеников. Можно ли назвать данную связь зависимостью? Что, в таком случае, будет являться независимой переменной, а что зависимой?
|
|
|
ТЕМА №9. Параметрические критерии различий.
9. 1. Понятие о параметрических критериях.
Критерии носят название «параметрические», потому что в формулу их расчёта включаются такие параметры выборки, как среднее, дисперсия и др. Таким образом, необходимо, чтобы распределение выборочных значений было близко к нормальному. Установлению данного факта, то есть выявлению согласия эмпирического распределения с нормальным, посвящён параграф 9. 3.
Как правило, в психологических исследованиях чаще всего применяются два параметрических критерия.
1. t-критерий Стьюдента. Направлен на оценку различий величин средних 
и 
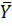двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причём выборки могут быть не равными по величине.
2. F-критерий Фишера. Позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений. Сравниваемые выборки должны быть распределены по нормальному закону. Измерение может быть произведено в шкале интервалов или отношений.
В данном пособии рассматривается t-критерий Стьюдента применительно к случаям связных и несвязных выборок. Критические значения (для уровней значимости 0, 05, 0, 01 и 0, 001) критерия приведены в Таблице 9 раздела «Таблицы критических значений». Критические значения зависят от числа степеней свободы k, рассчитываемого по определённому правилу.
9. 2. t-критерий Стьюдента.
Назначение и описание критерия
Критерий предназначен для сопоставления двух выборок, распределённых по нормальному закону. Выборки могу быть связными или несвязными, равными по величине или неравными. t-критерий Стьюдента основан на оценке различий величин средних двух выборок. Формула для расчёта по t-критерию Стьюдента в общем виде такова:
|
|
|
tэмп = 
,
где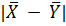 
- модуль разности средних арифметических переменных X и Y;
Sd =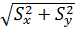 
.
В общем виде формула для расчёта Sd выглядит следующим образом:
Sd=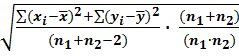 
,
где n1 и n2 – объёмы выборок X и Y;
- квадраты отклонений значений величин от средней.
Критические значения критерия зависят от числа степеней свободы, которое рассчитывается по формуле:
|
|
|
