 |
Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе
|
|
|
|
В случае поперечного изгиба в сечениях балки возникают не только изгибающий момент, но и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения.
Так как касательные напряжения в общем случае распределены по сечению неравномерно, то при поперечном изгибе поперечные сечения балки, строго говоря, не остаются плоскими. Однако при 
(где h - высота поперечного сечения, l - длина балки) оказывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плоских сечений и в случае чистого изгиба с достаточной точностью приемлема. Поэтому для расчета нормальных напряжений 
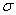применяют ту же формулу (5).
Рассмотрим вывод расчетных формул для касательных напряжений. Выделим из бруса, испытывающего поперечный изгиб, элемент длиной 
(рис. 6.28, а).
Рис. 6.28
Продольным горизонтальным сечением, проведенным на расстоянии y от нейтральной оси, разделим элемент на две части (рис. 6.28, в) и рассмотрим равновесие верхней части, имеющей основание шириной b. При этом с учетом закона парности касательных напряжений, получим, что касательные напряжения в поперечном сечении равны касательным напряжениям, возникающим в продольных сечениях (рис. 6.28, б). С учетом данного обстоятельства и из допущения о том, что касательные напряжения по площади 
распределены равномерно, используя условие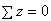 
, получим:
,
откуда
. (13)
где 
- равнодействующая нормальных сил 
в левом поперечном сечении элемента в пределах заштрихованной площади 
:
. (14)
С учетом (5) последнее выражение можно представить в виде
, (15)
где 
- статический момент части поперечного сечения, расположенной выше координаты y (на рис. 6.28,б эта область заштрихована). Следовательно, (15) можно переписать в виде
|
|
|
,
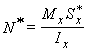откуда
. (16)
В результате совместного рассмотрения (13) и (16) получим
,
или окончательно
. (17)
Полученная формула (17) носит имя русского ученого Д.И. Журавского.
Условие прочности по касательным напряжениям:
, (18)
где 
-максимальное значение поперечной силы в сечении; 
- допускаемое касательное напряжение, оно, как правило, равно половине 
.
Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим из состава балки вокруг исследуемой точки элементарную призму (рис. 6.28, г), таким образом, чтобы вертикальная площадка являлась частью поперечного сечения балки, а наклонная площадка составляла произвольный угол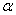 
относительно горизонта. Принимаем, что выделенный элемент имеет следующие размеры по координатным осям: по продольно оси - dz, т.е. по оси z; по вертикальной оси - dy, т.е. по оси у; по оси х - равный ширине балки.
Так как вертикальная площадка выделенного элемента принадлежит поперечному сечению балки, испытывающему поперечный изгиб, то нормальные напряжения 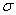на этой площадке определяются по формуле (5), а касательные напряжения 
- по формуле Д.И. Журавского (17). С учетом закона парности касательных напряжений, легко установить, что касательные напряжения на горизонтальной площадке также равны . Нормальные же напряжения на этой площадке равны нулю, согласно уже известной нам гипотезе теории изгиба о том, что продольные слои не оказывают давления друг на друга.
Обозначим величины нормальных и касательных напряжений на наклонной площадке через 
и 
, соответственно. Принимая площадь наклонной площадки 
, для вертикальной и горизонтальной площадок будем иметь 
и 
, соответственно.
Составляя уравнения равновесия для элементарной вырезанной призмы (рис. 6.28, г), получим:
|
|
|
,
откуда будем иметь:
;
.
Следовательно, окончательные выражения напряжений на наклонной площадке принимают вид:
.
Определим ориентацию площадки, т.е. значение 
, при котором напряжение 
принимает экстремальное значение. Согласно правилу определения экстремумов функций из математического анализа, возьмем производную функции от 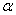и приравняем ее нулю:
.
Предполагая , получим:
.
Откуда окончательно будем иметь:
.
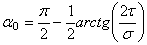Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения - главными напряжениями.
Сопоставляя выражения и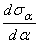 
, имеем:
,
откуда и следует, что касательные напряжения на главных площадках всегда равны нулю.
В заключение, с учетом известных тригонометрических тождеств:
и формулы 
,
определим главные напряжения, выражая из через 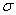и :
.
Полученное выражение имеет важное значение в теории прочности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу.
Пример 8.
В качестве примера применения формулы Журавского построим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки (рис. 6.29). Учитывая, что для этого сечения
получаем
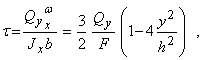
где 
- площадь прямоугольника.
Как видно из формулы, касательные напряжения по высоте сечения меняются по закону квадратической параболы, достигая максимума на нейтральной оси
Рис. 6.29
В круглом сечении (рис. 6.29) эпюра касательных напряжений ограничена кривой, имеющей максимум на нейтральной оси. Учитывая, что статический момент полукруга и момент инерции круга
,
получаем
Следовательно, максимальные касательные напряжения в круглом сечении на 33% больше средних напряжений 
, по которым, например, обычно проводится расчет заклепок.
Для треугольного сечения с основанием b и высотой h (рис. 6.29), имеем
,
Максимальное напряжение имеет место на расстоянии 
от нейтральной линии, то есть в точках средней линии треугольника.
Пример 9.
|
|
|
