Классификация термодинамических процессов

Классификация термодинамических процессов

Термодинамический процесс может быть задан либо графическим способом в виде изображения процесса в координатах p-v, p-T, Т-s, либо в аналитической форме в виде зависимости .

Уравнение процесса может быть также задано исходным условием о неизменном значении в этом процессе какой - либо функции состояния ( ) или условием о равенстве нулю какого – либо эффекта термодинамического процесса , однако и в этом случае исходное условие приводится к основной форме уравнения процесса.

При изучении термодинамических процессов определяются:

1) закономерность изменения параметров состояния рабочего тела, то есть выводится уравнение процесса или дается его графическое изображение в координатах p-v,  p-T,  Т-s и т. д.;

2) параметры состояния системы в начальной и конечной точках процесса;

3) численные значения работы и теплообмена в процессе;

4) изменение значений внутренней энергии, энтальпии и энтропии рабочего тела.

Простейшие термодинамические процессы

Простейшими термодинамическими процессами обычно считают изобарный, изохорный и изопотенциальные процессы.

Изобарный процесс ( 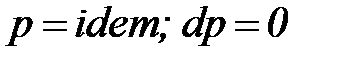) – процесс в котором давление в системе остается постоянным.

Изобарный процесс (или изобара) графически представлен на рис. 5.

 

Рис. 1. 5. Графическое представление изобарного процесса.

 

В изобарных процессах происходит увеличение (1-2) или уменьшение удельного объема, что связано изменением температуры, обусловленным подводом или отводом теплоты.

Изобарные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых, холодильных установках и др.

Для идеального газа в изобарном процессе (1-2) значение удельного объема прямо пропорционально температуре рабочего тела .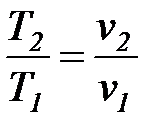

Удельная термодинамическая и потенциальная работы в изобарном процессе определяются из соотношений

 

,                            (1. 67)

В случае идеального газа в силу 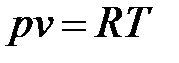  имеем

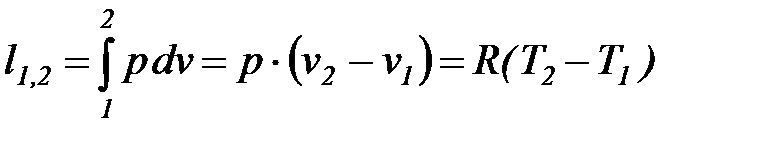                       (1. 68)                                                      

 

Количество теплоты, подведенной к рабочему телу или отведенной от него в изобарном процессе, определяется из выражения первого начала термодинамики

 

.                                        (1. 69)

 

Изохорный процесс ( 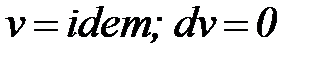) – процесс, при котором объем системы или удельный объем рабочего тела остается постоянным (рис. 6).

 

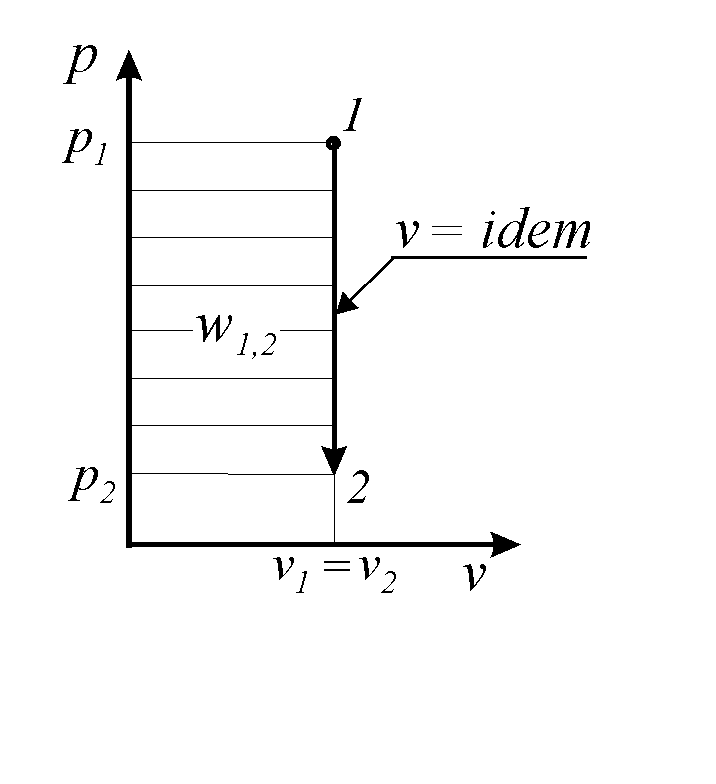
Рис. 1. 6. Графическое представление изохорного процесса.

 

В изохорных процессах происходит уменьшение (1-2) или увеличение давления, что связано с соответственным изменением температуры – подводом или отводом теплоты.

Изохорные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых установках и др.

Для идеального газа в изохорном процессе (1-2) давление прямо пропорционально температуре рабочего тела .

Удельная термодинамическая и потенциальная работы в изохорном процессе определяются из соотношений

 

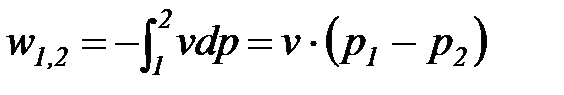
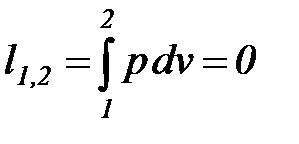.                     (1. 70)

В случае идеального газа в силу 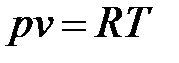  имеем

 

.                       (1. 71)

 

Количество теплоты, подведенной к рабочему телу или отведенной от него в изохорном процессе, определяется из выражения первого начала термодинамики

 

.                                     (1. 72)

 

Изопотенциальный процесс – термодинамический процесс измене-

ния состояния системы, при котором значение потенциальной функции ( ) сохраняет неизменное значение. Для идеального газа, согласно уравнению Клапейрона ( ), изопотенциальный процесс является и изотермическим ( 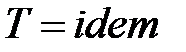) (рис. 1. 7).

 

Рис. 1. 7. Графическое представление изопотенциального

процесса.

 

Удельная термодинамическая и потенциальная работы в изопотенциальном процессе (1-2) определяются из следующих соотношений:

 

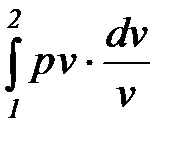=  = ;                             (1. 73)

 

 = = = .                 (1. 74)

 

Нетрудно заметить, что постоянство потенциальной функции ( ) приводит к равенству логарифмов в выражениях (1. 73) и (1. 74) в силу того, что соблюдается условие . Поэтому, в изопотенциальном процессе численные значения термодинамической и потенциальной работ равны между собой.

Количество теплоты, подведенной к рабочему телу или отведенной от него в изопотенциальном процессе определяется из выражения первого начала термодинамики по балансу рабочего тела

 

.                                  (1. 75)

 

 

Адиабатический процесс – термодинамический процесс измене-

ния состояния системы, при котором теплообмен равен нулю ( 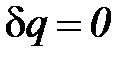)   и, в силу обратимости процесса, энтропия остается величиной постоянной

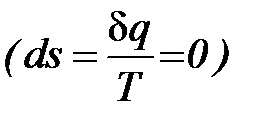, таким образом адиабатический процесс является и изоэнтропийным (рис. 1. 8).

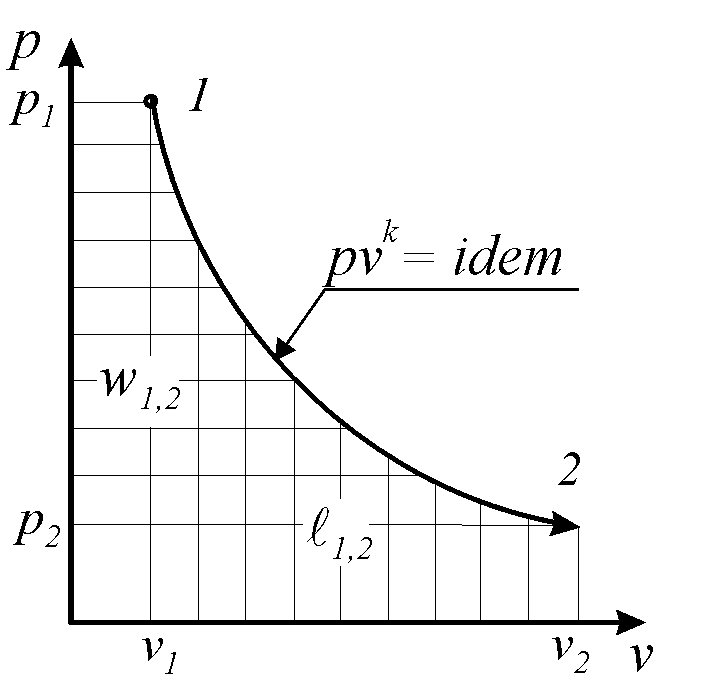
Рис. 1. 8. Графическое представление адиабатического

процесса.

 

Уравнение и показатель адиабатического процесса может быть получено из выражения первого начала термодинамики для простого тела. При условии, что теплообмен равен нулю имеем:

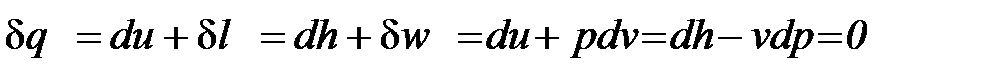               (1. 76)

 

Разделяя переменные получим выражение для определения показателя адиабатического процесса

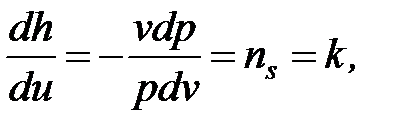
 (1. 77)

 

где n_s=k – показатель адиабаты.

Расчетное выражение для расчета показателя адиабатного процесса

 

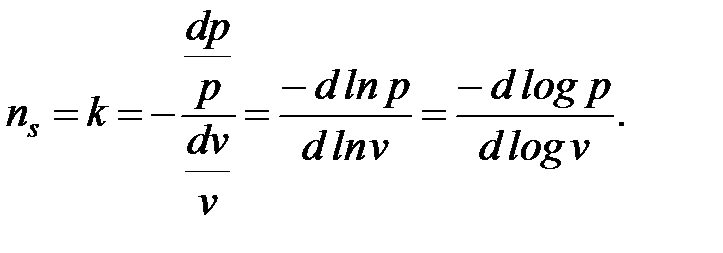
(1. 78)

 

 

После интегрирования при условия постоянства показателя процесса имеем

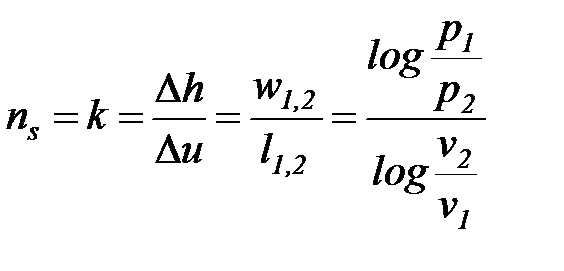
(1. 79)

 

Для идеального газа показатель адиабаты равен k= c_p/c_v.

 Уравнения перечисленных простейших и любых других термодинамических процессов могут быть представлены одним уравнением. Это уравнение называется уравнением политропы, а термодинамические процессы, описываемые этим уравнением, называются политропными.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: