 |
Работа в политропных процессах простых тел
|
|
|
|
Работа в политропных процессах простых тел
Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах можно получить при сопоставлении их элементарных значений:
 ; (1. 92)
; (1. 92)
 . (1. 93)
. (1. 93)
После подстановки выражения для показателя политропы (1. 84) в соотношение (1. 93) получаем
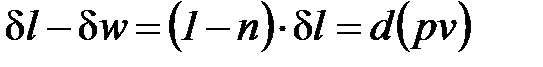 , (1. 94)
, (1. 94)
или
 . (1. 95)
. (1. 95)
Интегрируя последнее выражение (1. 95) с учетом того, что процесс подчиняется уравнению политропы с постоянным показателем (n=idem), получаем следующее соотношение для определения удельной термодинамической работы в конечном процессе (1-2)
 . (1. 96)
. (1. 96)
Введем понятие характеристики процесса расширения или сжатия, определяемой соотношением
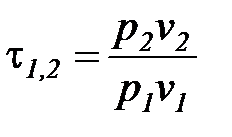 . (1. 97)
. (1. 97)
С учетом соотношений (1. 84), (1. 97), зависимости для определения удельной термодинамической и потенциальной работы в конечном процессе примут следующий вид:
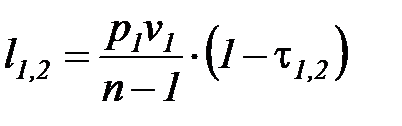 ; (1. 98)
; (1. 98)
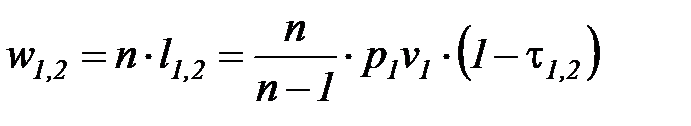 . (1. 99)
. (1. 99)
Соотношение для определения характеристики расширения или сжатия в рассматриваемом процессе 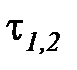 определяется с учетом зависимостей (1. 80), (1. 81) и имеет следующий вид:
определяется с учетом зависимостей (1. 80), (1. 81) и имеет следующий вид:
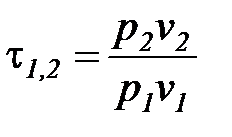 =
=  =
= 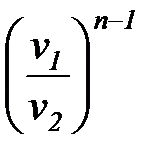 . (1. 100)
. (1. 100)
Теплообмен в термодинамических процессах простых тел
Теплообмен в любом термодинамическом процессе изменения состояния простых тел может быть выражен в зависимости от величины термодинамической или потенциальной работы процесса. При этом термодинамический процесс в общем случае рассматривается как политропа с переменным показателем.
|
|
|
Расчетное выражения теплообмена для простых тел выводится на основе рассмотрения выражения первого начала термодинамики
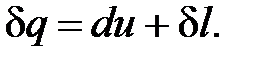 (1. 101)
(1. 101)
Удельная внутренняя энергия для простых тел может быть представлена в виде функции любых двух независимых параметров состояния. Примем, что u =и (p, v). Тогда дифференциал внутренней энергии запишется в следующем виде:
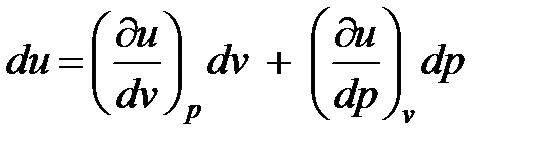 . (1. 102)
. (1. 102)
Последнее выражение (1. 101) можно представить в виде
 . (1. 103)
. (1. 103)
Введем следующие обозначения:
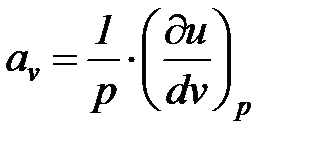 ;
;  . (1. 104)
. (1. 104)
При этом выражение (1. 103) примет вид:
 . (1. 105)
. (1. 105)
Сопоставляя соотношения (1. 101) и (1. 105), получим
 (1. 106)
(1. 106)
Для определения величин (  и
и  ) рассмотрим два термодинамических процесса:
) рассмотрим два термодинамических процесса:
1. Изоэнергетический процесс (u = idem, du = 0). Для этого процесса показатель политропы принимает значение n = nu.
Так как в изоэнергетическом процессе 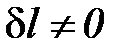 , из уравнения (1. 105) следует, что
, из уравнения (1. 105) следует, что
 (1. 107)
(1. 107)
или
 . (1. 107а)
. (1. 107а)
2. Адиабатный процесс(d q = 0). В этом процессе показатель политропы принимает значение n = k и называется показателем адиабаты.
В адиабатном процессе элементарная термодинамическая работа также не равна нулю, поэтому из выражения (1. 106) имеем
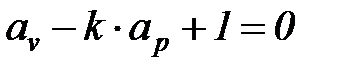 . (1. 108)
. (1. 108)
Сопоставляя соотношения (1. 107) и (1. 108), получаем следующие выражения:
 ,
,  . (1. 109)
. (1. 109)
С учетом полученных соотношений для определения av и ap, находим выражения для расчета удельных значений изменения внутренней энергии и теплообмена в элементарном процессе:
|
|
|
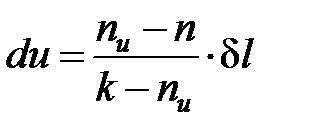 , (1. 110)
, (1. 110)
 . (1. 111)
. (1. 111)
Соотношения для расчета удельных значений изменения внутренней энергии и теплообмена в конечном процессе имеют следующий вид:
 , (1. 112)
, (1. 112)
 . (113)
. (113)
Полученные соотношения (1. 112), (1. 113) позволяют в координатах p-v построить области подвода и отвода теплоты (рис. 1. 1).

| Рис. 1. 11. Процессы изменения состояния идеального газа |
Некоторые характеристики важнейших термодинамических процессов приведены в табл. 1. 1
Таблица 1. 1
Термодинамические процессы изменения состояния простого тела
| Название и уравнение процесса | Показатель политропы | Графическое изображение | Работа | Количество теплоты |
| Политропный pvn = idem | -¥ £ n £ +¥,
n = 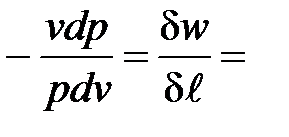
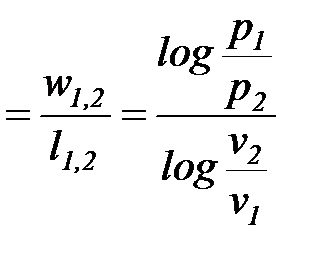
| | l1, 2 =  ,
w1, 2 = n ,
w1, 2 = n 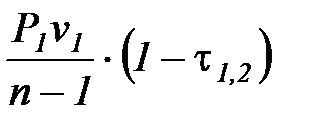 ,
t1, 2 = ,
t1, 2 = 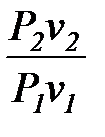 = =  =
= =
= 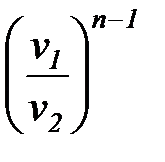 = = 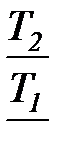
| q1, 2 = Du1, 2 + l1, 2 =
= Dh1, 2 + w1, 2,
q1, 2 = 
|
| Изобарный p = idem, dp = 0 | n = 0 |
| l1, 2= p× (v2 - v1),
w1, 2= 0,
t1, 2 = 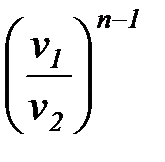 = = 
| q1, 2 = Du1, 2 + l1, 2 = = Dh1, 2 |
Продолжение табл. 1
| Изохорный v = idem, dv = 0 | n = ± ∞ | | l1, 2 = 0,
w1, 2 = v× (p1 - p2),
t1, 2 = 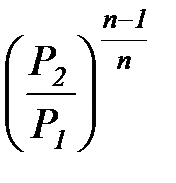 = = 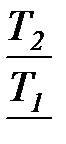
| q1, 2 = Du1, 2 = = Dh1, 2 + w1, 2 |
| Изопотенциаль-ный pv = idem | n = 1 | |
l1, 2 = w1, 2 =
= pv× ln  = pv× ln = pv× ln  ,
t1, 2 = 1 ,
t1, 2 = 1
| q1, 2 = Du1, 2 + l1, 2 = = Dh1, 2 + w1, 2 |
| Адиабатный δ q = 0, pvk = idem | n = k = ns =
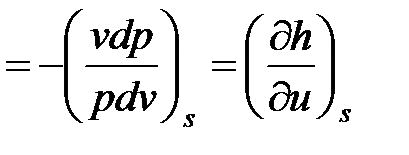
| | l1, 2 = 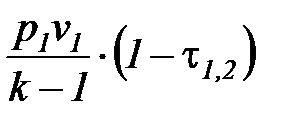 ,
w1, 2 = k× ,
w1, 2 = k×  ,
t1, 2 = ,
t1, 2 = 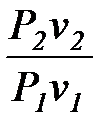 = = 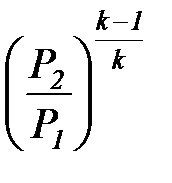 =
= =
= 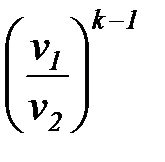 = = 
| q1, 2 = 0 |
|
|
|


