 |
Политропные процессы
|
|
|
|
Термин «политропа» представляет собой сочетание двух греческих слов «поли» - много и «тропос» - путь, направление. Поэтому в политропном процессе предполагается многообразие путей изменения параметров состояния системы.
Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела, подчиняющийся уравнению, которое может быть представлено в следующих формах:
; (1. 80)
; (1. 81)
= 
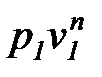. (1. 82)
где п – показатель политропы, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (-¥ £ n £ +¥ ).
Физический смысл показателя политропы п определяется после дифференцирования выражения (1. 80)
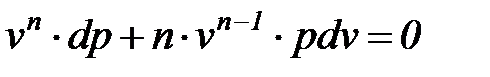. (1. 83)
Из соотношения непосредственно следует
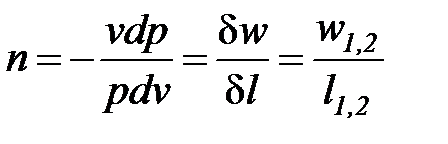. (1. 84)
Это значит, что постоянный показатель политропы определяется соотношением потенциальной и термодинамической работ в элементарном или конечном процессах. Значения этих работ могут быть определены графически в координатах 
(рис. 1. 9а).
В логарифмических координатах политропный процесс (политропа) с постоянным показателем представляет собой прямую линию (рис. 1. 9б)
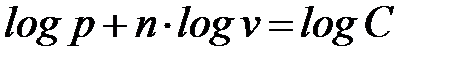. (1. 85)
При этом, постоянный показатель политропы определяется как тангенс угла наклона линии процесса к оси абсцисс (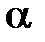 
) (рис. 1. 9б)
n =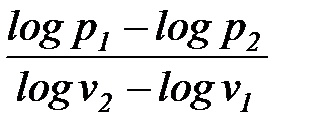 
= 
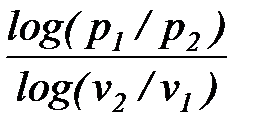. (1. 86)
|
|
|
а б
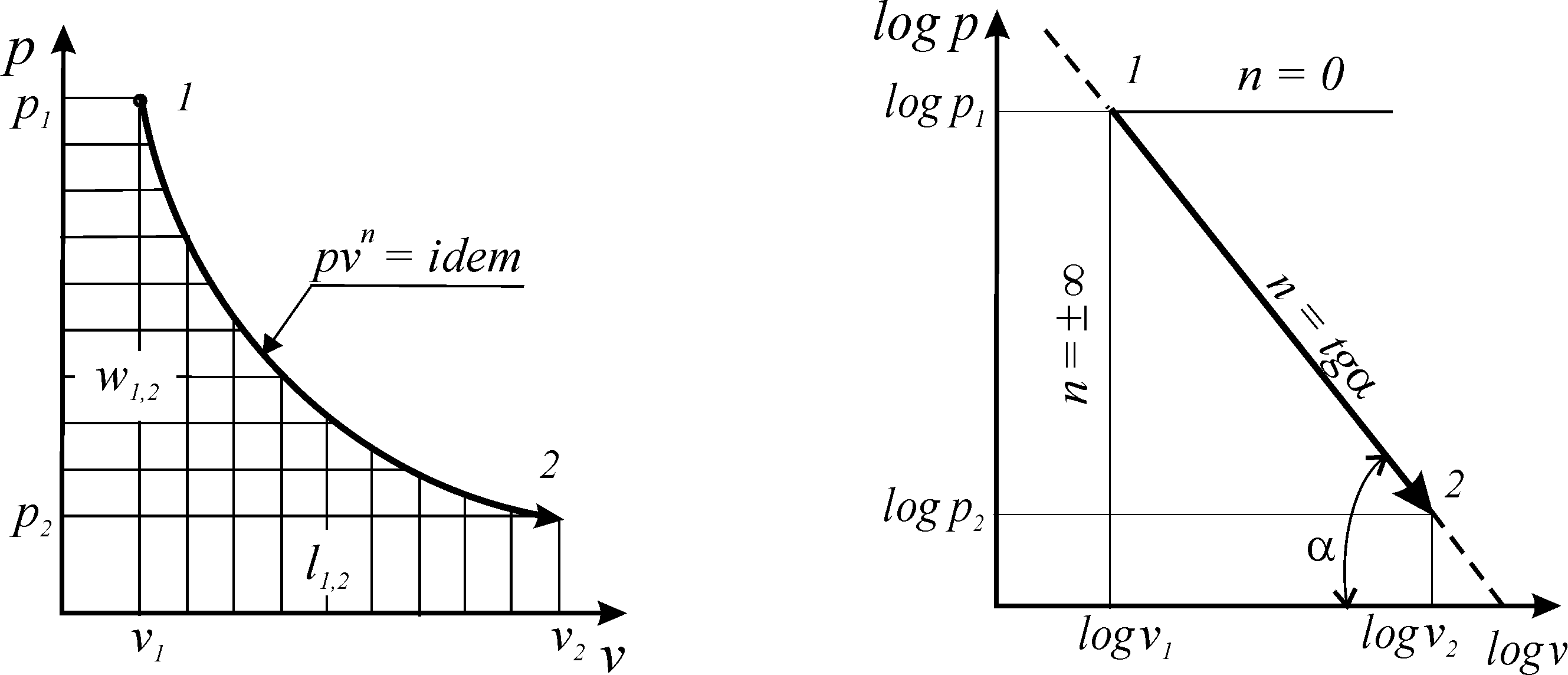
Рис. 1. 9. Политропа с постоянным показателем
Из соотношения (1. 83) следует, что для изобарного процесса n = 0,
для изохорного процесса - n = ± ∞ , для изопотенциального
процесса - n = 1.
Следует отметить, что не все термодинамические процессы в координатах logv – logp описываются прямой линией, т. е. подчиняются уравнению политропы с постоянным показателем. Любой термодинамический процесс можно описать уравнением политропы с переменным показателем (рис. 1. 10).
Расчет политропного процесса с переменным показателем вызывает необходимость ввести в рассмотрение три показателя процесса: истинный показатель процесса (n); первый средний показатель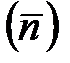 
и второй средний показатель (m).
Истинный показатель процесса (n) определяется как соотношение элементарной потенциальной работы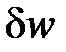 
к элементарной термодинамической работе 
, что соответствует тангенсу угла наклона касательной, проведенной к кривой процесса в точке процесса, к оси абсцисс ( 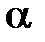) в логарифмической сетке координат.
n =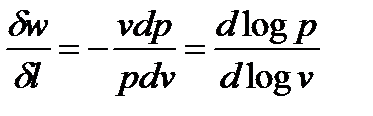 
= tga. (1. 87)
| Рис. 1. 10. Политропа с переменным показателем |
Для конкретных процессов, характеризующихся неизменным значением какой-либо функции или параметра состояния (z = p, v, T, u, h, s), истинный показатель политропы определяется соотношением
. (1. 88)
Первый средний показатель политропы определяется как отношение конечных (интегральных) значений потенциальной и термодинамической работ в процессе
. (1. 89)
Второй средний показатель политропы численно равен тангенсу угла наклона секущей 1-2 к оси абсцисс ( 
) в логарифмической сетке координат (рис. 1. 10)
|
|
|
m = 
= 
. (1. 90)
Непосредственно из последнего выражения (1. 90) следует уравнение политропы с переменным показателем
. (1. 91)
При проведении инженерных расчетов в ряде случаев политропные процессы с переменным показателем политропы приближенно описываются уравнением политропы с постоянным показателем (1. 79), значение которого принимается равным первому среднему показателю политропы ( 
).
|
|
|
