Тема 4. Теория неопределенности и асимметрия информации

 

4.1 Основные понятия неопределенности и риска

4.2 Оценка расположенности к риску

4.3 Рыночные решения в условиях неопределенности

 

4.1 Основные понятия неопределенности и риска

В теории потребительского поведения все величины (цены, доходы, количества) в основном рассматривались как точно определенные. Теория полезности использовалась как средство прогнозирования потребительского выбора из некоторого количества известных альтернатив. Однако часто потребительский выбор (при страховании, покупке акций, выборе места работы и т.п.) связан со значительной неопределенностью, и потребители вынуждены выбирать из альтернатив, отличающихся степенью риска. Эта неопределенность характеризуется понятием риска, если известны каждый из возможных результатов и вероятность его осуществления.

С теоретической точки зрения очень важно объяснить, каким образом по­требители выбирают тот или иной вариант поведения в условиях нескольких альтернатив, как они реагируют на элемент риска, какую он играет роль при осуществлении ими своего выбора. В рамках теории полезности необходимо выяснить, возможно ли рационализировать это поведение и что именно будет максимизировать рациональный потребитель.

Дж. фон Нейман и О. Моргенштерн в фундаментальном труде «Те­ория игр и экономическое поведение» (1943) дали формальное доказатель­ство того, что принцип максимизации ожидаемой полезности является крите­рием рациональности ожидаемых решений. Они разработали систему аксиом количественной полезности, из которых следует существование такой функ­ции полезности, математическое ожидание значений которой согласовано с предпочтениями субъекта. Иными словами, потребитель в состоянии опреде­лить, что предпочтительнее: набор благ или лотерейный билет.

Прежде чем приступить к более глубокому изучению проблемы потреби­тельского выбора в условиях риска и неопределенности, следует определить эти понятия.

Неопределенность – это ситуация, при которой полностью или частично отсутствует информация о вероятных будущих событиях, то есть неопределен­ность – это то, что не поддается оценке.

Риск – это определенная любым способом вероятность совершения каждого из воз­можных событий, т.е. ситуация, противоположная неопределенности.

Следовательно, в условиях неопределенности выбора потребитель максимизирует ожидаемую полезность, т.е. средневзвешенную полезность всех возможных результатов с учетом вероятности достижения каждого из них.

Чтобы количественно измерить риск, надо знать все возможные послед­ствия какого-нибудь отдельного действия и вероятность самих последствий. Вероятность означает возможность получения определенного результата. Различают два типа вероятности: 1) математическую или априорную; 2) статистическую.

Математическая вероятность (априорная) определяется общими, заранее заданными прин­ципами (например, вероятность выпадения числа) и очень редко встречается в экономике.

Статистическая вероятность (апостериорная) определяется эмпирически (опытным путем), и именно она наиболее часто встречается при решении экономических проблем. Она представляет собой трудную для формулировки концепцию, так как может за­висеть как от природы неопределенных событий, так и от надежд, которые индивиды возла­гают на них. При ее определении могут быть использованы:

1) объективная вероятность, основанная на вычислении частоты, с которой про­исходят некоторые события (предположим, из ста случаев двадцать имеют какой-либо положительный результат, следовательно, вероятность этого результата составляет 20 %, что является объективным показателем);

2) субъективная вероятность, которая представляет собой предположение относительно определенного результата, основанного на суждении или личном опыте оценивающего. В этом случае различные индивиды могут уста­навливать разное ее значение для одного и того же события и таким обра­зом делать различный выбор. Определяющим фактором здесь выступает наличие информации.

Как объективная, так и субъективная вероятность используется при опре­делении двух важных критериев, которые помогают описывать и сравнивать степень риска. Один из критериев характеризует среднеезначение, а другой – изменчи­вость возможного результата.

Среднее значение определяется обычно как среднеарифметическое взве­шенное, где вероятность каждого результата используется в качестве частоты или веса соответствующего значения. Иногда употребляют термин «ожидае­мое значение». Оно определяется как:

(4.1)

,

 

где – возможный результат;

– вероятность его достижения ().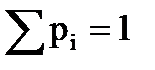

 

Изменчивость обычно измеряется двумя связанными критериями:

1) дисперсия – средневзвешенное из квадратов отклонений действительных результатов от ожидаемых;

2) стандартное (среднее квадратичное) отклонение – квадрат­ный корень из дисперсии.

Дисперсионный метод успешно применяется при наличии как двух, так и большего количества альтернативных результатов.

На основе формулы (4.1) Нейманом и Моргенштерном в теорию неопределенности было введено понятие ожидаемой полезности – это средневзвешенная полезность всех возможных результатов, где в качестве весов используются вероятности результатов. Они показали, что лицо принимающее решение (ЛПР) при принятии решения будет стремиться к максимизации ожидаемой полезности. Другими словами, из всех возможных решений он выберет то, которое обеспечивает наибольшую ожидаемую полезность. В этой связи определение полезности по Нейману-Моргенштерну формулируется как некоторое число, приписываемое ЛПР каждому возможному исходу (т.е. значение (4.1), соответствующее полезности конкретного набора благ). Ими была предложена процедура построения индивидуальной функции полезности, которая заключается в следующем: ЛПР отвечает на ряд вопросов, обнаруживая при этом свои индивидуальные предпочтения, учитывающие его отношение к риску. Значения полезностей могут быть найдены за два шага.

Шаг 1. Присваиваются произвольные значения полезностей выигрышам для худшего и лучшего исходов, причем первой величине (худший исход) ставится в соответствие меньшее число.

Шaг 2. Игроку предлагается на выбор: получить некоторую гарантированную денежную сумму v, находящуюся между лучшим и худшим значениями, либо принять участие в игре, т.е. получить с вероятностью р наибольшую денежную сумму S и с вероятностью (1 – р) – наименьшую сумму s. При этом вероятность следует изменять (понижать или повышать) до тех пор, пока ЛПР станет безразличным в отношении к выбору между получением гарантированной суммы и игрой.

Пусть указанное значение вероятности равно р₀. Тогда полезность гарантированной суммы определяется как среднее значение (математическое ожидание) полезностей наименьшей и наибольшей сумм, т.е.

(4.2)

U(v) = p₀∙U(S) + (1 – p₀)∙U(s).

 

Таким образом, если определена шкала измерения, то может быть построена функция полезности ЛПР.

 

4.2 Оценка расположенности к риску

После определения теоретических понятий необходимо определить, в какой мере различается отношение к риску. Все индивиды различаются своей готовностью пойти на риск: некоторые не хотят рисковать, другие – наоборот, третьи к риску безразлич­ны (нейтральны). В этой связи Нейман и Моргенштерн выявили три типа функций полезности при оценке расположенности к риску.

Наиболее распространенное отношение к риску – это нерасположен­ность к нему. Достаточно сослаться на огромное число рискованных ситуа­ций, когда индивиды заключают договоры страхования, ищут работу с относительно стабильной заработ­ной платой. Следовательно, противником риска считается индивид, который при данном ожидаемом доходе предпочитает определенный гарантирован­ный результат ряду неопределенных рисковых результатов. Графически эта ситуация выглядит следующим образом (рис. 4.1).

 

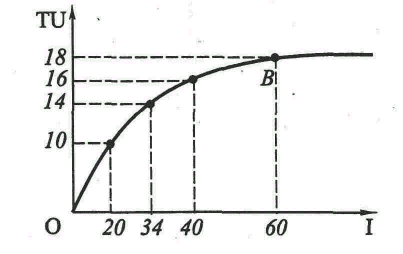
Рисунок 4.1 – Кривая нерасположенности к риску

 

Кривая ОВ задает функцию общей полезности (TU) и указывает на уровень полезности, который может достигаться при каждом уровне дохода I (используется в качестве ожидаемой денежной оценки полезности). Уровень полезности рас­тет с 10 до 14 и далее до 16 и 18 единиц (ютилей) при росте дохода, соответственно с 20 до 34 ден. ед. и далее до 40 и 60 ден. ед. Следовательно, предельная полезность снижается с ростом дохода.

Предположим, что можно выбрать работу со стабильным до­ходом в 40 ден. ед. или работу, доход от которой связан с риском, т.е., например, с одинако­вой вероятностью 0,5 его доход может увеличиться до 60 ден. ед. или снизиться до 20 ден. ед.

Согласно рис.4.9, уровень общей полезности при доходе 20 ден. ед. ра­вен 10, а при доходе 60 ден. ед. – 18. Так как ожида­емая полезность является суммой полезностей, связанных со всеми возмож­ными результатами, взвешенных по вероятности каждого результата (см. формулу (4.1)), то ее величина равна . Однако стабильный доход в 40 ден. ед. дает полезность, равную 16, что больше, чем ожидаемая полезность при работе, связанной с риском.

Таким образом, поведение противников риска согласуется с принципом убывания предельной полезности. Уклонение от риска является рациональным поведением, максимизирующим совокупную полезность. Индивиды, нерасположенные к риску, готовы пойти на него лишь в том случае, если им предложат соответствующую компенсацию.

Нейтральным к риску считается индивид, который при данном ожидаемом доходе безразличен к выбору между гарантированным и рискованным результатами. Графически это выражено на рис. 4.2.

В данном случае полезность работы, связанной с риском, составляет , что равно полезности работы, связанной с получением стабильного дохода.

Склонным к риску считается человек, который при данном ожидаемом доходе предпочитает связанный с риском результат определенному гарантированному результату. Графически это отражено на рис. 4.3.

 

Рисунок 4.2 – Кривая нейтрального отношения к риску

Рисунок 4.3 – Кривая расположенности к риску

В числовом выражении ожидаемая полезность от рискованного решения составит . Это выше, чем полезность с гарантированным результатом 40 ден. ед. (равна 8 ед. согласно рис. 4.3).

Вознаграждением за риск является сумма денег, которую человек, не склонный к риску, готов заплатить, чтобы избежать его. Эта вели­чина зависит от тех связанных с риском альтернативных вариантов, с кото­рыми он сталкивается. Так, в примере, соответствующем рис. 4.1, возна­граждение за риск равно 6 ден. ед. Эта цифра определяется следующим образом: ожидаемая полезность, равная 14, достигается субъектом, рассматриваю­щим возможность выхода на связанную с риском работу с ожидаемым сред­ним доходом 40 ден. ед., что определено по формуле расчета средневзвешенной полезности. Однако этот же уровень полезности может быть достигнут при стабильном доходе 34 ден. ед., как следует из рис.4.9. Таким образом, 6 ден. ед. составляют ту величину дохода (40 – 34), которым он готов пожертво­вать, предпочитая работу со стабильным доходом рискованному заработку.

Чем больше изменчивость доходов (т.е. дисперсия), тем больше индивид, не расположенный к риску, готов заплатить, чтобы избежать этих рискованных вариантов.

 

4.3 Спрос на рисковые активы в условиях неопределенности

Большинство индивидов не склонны к риску, однако многие вкладывают свои сбережения в активы, связанные с риском. Чтобы выяснить, как происходит процесс принятия решений в условиях неопределенности, надо определить ряд связанных понятий.

Активы – это средства, обеспечивающие денежные поступле­ния их владельцу в форме как прямых выплат (прибыль, дивиденды, рента и т. д.), так и скрытых (увеличение стоимости фирмы, недвижимо­сти, акций и т. д.). Они подразделяются на безрисковые (денежные поступления от них заранее известны) и рисковые (доход по ним частично зависит от случая). Пример безрисковых активов – государственные облигации, а рисковых – акции промышленных предприятий, банков и т. п.

Целью приобретения активов является получение дохода.Чтобы оп­ределить, какой из них выгоднее, надо сопоставить денежные поступления от них с их ценой. Таким образом, прибыль от актива представляет собой отноше­ние общего объема денежных поступлений от актива к его цене. Например, облигация, цена которой составляет на данный момент 1000 ден. ед., приносит в данном году 100 ден. ед. поступлений, что означает, что она приносит 10 % прибыли.

Вкладывая свои сбережения в акции, облигации и другие активы, индивиды рас­считывают на получение прибыли, которая превышает уровень инфляции. В этом случае, откладывая свое потребление, они смогут в будущем купить больше, чем в данный момент, расходуя весь свой доход. Следовательно, при­быль от активов должна быть определена в реальном (с поправкой на инфля­цию) выражении. Реальная прибыль от актива представляет собой номиналь­ную прибыль за вычетом инфляции. Например, если уровень инфляции составляет 5 % в год, то реальная прибыль от рассмотренной выше облигации будет 5 %.

Сравнение рисковых активов осуществляется с помощью расчета ожидаемой прибыли (то есть прибыли, ко­торую актив принесет в среднем). Существует связь между ожидаемой прибылью и риском: чем выше прибыль на капиталовложения, тем выше риск. Рассмотрим эту взаимосвязь более подробно на примере задачи оптимизации инвестиционного портфеля.

Предположим, что у индивидуума есть желание вложить все свои сбереже­ния в два актива: облигации государственного займа; акции банка. В этом случае надо решить, какую часть сбережений вложить в каждый из них. Разрешение этой проблемы аналогично решению проблемы потребительского выбора при распределении бюджета на покупку потребительских товаров.

Пусть свободная от рисков прибыль по облигациям – R_f, а ожидаемая при­быль от акций – R_m. При при­нятии решения о вложении капитала известен ряд возможных результатов и вероятность каждого, но неизвестно, какой именно из этих результатов осуще­ствится. У рисковых активов пусть будет более высокая прибыль, чем у безрис­ковых (R_m > R_f), иначе не склонные к риску вкладчики приобретали бы только облигации, а акции вообще бы не приобретались.

Чтобы определить, сколько денег вкладчик вложит в каждый вид актива, обозначим часть его сбережений, вложенных в акциях, через b, тогда часть, которая используется для покупки облигаций, будет 1 – b. Суммарная ожидаемая прибыль R_p от приобретенных ценных бумаг является средневзвешенной ожидаемой прибылью от этих двух активов:

(4.3)

.

 

Для определения степени риска следует вычислить дисперсию общей при­были от набора активов. В этом случае стандартное отклонение равно σ_p = b∙σ_m, где σ_m – стандартное отклонение прибыли от вклада в акции.

Однако наиболее важным является вопрос о том, каким образом вкладчик принимает решение относительно размера части b. Здесь он сталкивается со взаимозаменяемостью риска и прибыли при построении своей бюджетной линии.

Уравнение (4.3) для суммарной ожидаемой прибыли можно перепи­сать как

(4.4)

,

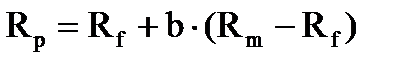(4.5)

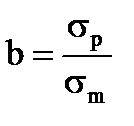причем , отсюда .

Последнее выражение является уравнением бюджетной линии, так как описывает взаимосвязь между риском и прибылью. Это уравнение пря­мой линии, из которой следует, что R_p возрастает по мере того, как стандарт­ное отклонение этой прибыли σ_p увеличивается. В этом случае величина угла наклона бюджетной линии называется ценой риска, так как она показывает, насколько возрастает риск инвестора, который намерен получить дополнительную прибыль.

Если вкладчик не желает рисковать, он может вложить все свои средства в облигации (b = 0) и получить прибыль R_f. Чтобы получить более высокую ожида­емую прибыль, он должен пойти на некоторый риск. Например, вложить все средства в акции (b = 1) и заработать прибыль R_m, но при этом риск увеличится, и стандартное отклонение составит σ_m. Или же он может вложить свои средства по частям в различные виды активов, получить прибыль в пределах R_m…R_f и иметь риск меньше σ_m, но больше нуля.

Эти выводы иллюстрируются на рис. 4.4, где показаны три кривые безразличия инвестора, каждая из которых дает сочета­ние размеров риска (σ) и прибыли (R), в равной степени удовлетворяющие вкладчика (кривые идут с наклоном вверх, так как риск нежелателен и его увеличение следует компенсировать повышением доходности). Кривая U₁ связана с максимальным удовлетворением вкладчика, а U₃ – с минимальным. При оди­наковом уровне риска ожидаемая прибыль на U₁, больше, чем на U₂ и U₃. Подобно потребителю, делающему выбор между двумя благами, вкладчик выберет сочетание риска и прибыли в точке, где кривая его безразличия будет явля­ться касательной по отношению к его бюджетной линии M (при этом его прибыль равна R^* и стандартное отклонение σ^*).

Rp U1 U2 M U3   R* Rf     σ* σ

 

 

 

Рисунок 4.4 – Выбор потребителя между величиной риска и прибыли

 

Эти же принципы принятия решения в условиях риска сохраняются, если для анализа будут взяты любые другие активы.

Максимальный размер риска, на который решится вкладчик, чтобы зарабо­тать более высокую ожидаемую прибыль, зависит от его отношения к риску. У склонных к риску вкладчиков наблюдается тенденция к включению большей доли рисковых активов в портфель ценных бумаг.

Поэтому обычно осуществляется диверсификация такого портфеля в качестве ме­тода снижения риска путем распределения инвестиций между несколькими рисковыми активами.

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: