1.4.2. Геометрическая интерпретация условия фазового равновесия

Основное термодинамическое условие фазового равновесия при р и Т -const (например, между твердой ( S ) и жидкой ( L ) фазами двойной системы) – это равенство химических потенциалов компонентов в каждой фазе, т. е. μ _A^S = μ _A^L и μ _В^S =μ _В ^L .

Геометрической интерпретацией условия фазового равновесия (при р и Т -const) является проведение общей касательной к концентрационным зависимостям свободной энергии Гиббса, построенным для каждой фазы. Точки касания соответствуют составу равновесных фаз.

Поясним данное утверждение. Химический потенциал – это парциальная молярная энергия Гиббса компонента в растворе.

(1. 20)

где: G – изобарно–изотермический потенциал раствора.

Химический потенциал данного компонента геометрически отображается тангенсом угла наклона касательной к кривой изобарно–изотермического потенциала раствора в точке соответствующей заданной концентрации.

Докажем, что для случая равновесия двух фаз равенство химических потенциалов компонентов отражает общая касательная к обеим кривым изобарно–изотермического потенциала, построенная для каждой фазы.

Рассмотрим двухкомпонентную систему А – В , в которой при некоторой температуре Т в равновесии находятся фазы жидких ( L ) и твердых ( S ) растворов (рис. 1. 3). Каждая из фаз образует непрерывный раствор во всем диапазоне концентраций и характеризуется собственной кривой зависимости свободной энергии Гиббса от состава: G^L и G^S соответственно.

Рис. 1. 3. Обоснование двухфазного равновесия методом проведения касательной

 

На рис. 1. 3 представлены:

G^oS_i и G^oL_i - свободные энергии Гиббса чистых компонентов в твердой ( S) и жидкой ( L ) фазах;

G^L – концентрационная кривая изобарно-изотермического потенциала жидкого раствора;

G^S – концентрационная кривая изобарно-изотермического потенциала твердого раствора;

аb – общая касательная

Предполагаем концентрацию компонента В ( x_B ) независимой, т. е. состав фаз определяем по компоненту В ( x_A+ x_B=1 ).

Условия проведения общей касательной к двум кривым следующие:

Первое условие - это равенство угловых коэффициентов в точках касания, его можно записать в виде:

(1. 21)

Это условие необходимое, но недостаточное, т. к. касательные к двум кривым могут иметь одинаковый наклон, но на разных уровнях. Отсюда вытекает второе условие: принадлежность точек касания одной и той же прямой. Исходя из геометрии (рис. 1. 3), второе условие можно выразить уравнением:

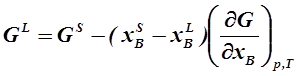
(1. 22)

Учитывая первое условие (1. 21), и, преобразуя выражение (1. 22), получим:

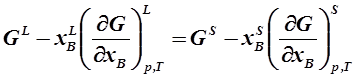
Используя для дальнейших преобразований уравнения Гиббса-Дюгема: G = x_Aμ _{A +} x_B μ _B и x_A(∂ μ _A/∂ x_B) + x_B(∂ μ _B/∂ x_B) = 0 , и выражение x_A+ x_B=1 , получаем:

(1. 23)

Тогда: G^L − x_B^L( μ ^L_B− μ ^L_A) = G^S − x_B^S( μ ^S_B − μ ^S_A)

или G^L − x_B^L μ ^L_B − x_А^L μ ^L_A + μ ^L_A = G^S − x_B^Sμ ^S_B − x_А^S μ ^S_A + μ ^S_A

т. е. μ ^L_A = μ ^S_A

Принимая в качестве независимой переменной концентрацию компонента А и повторяя ход рассуждений, получим:

μ LВ = μ SВ

Таким образом, проведение общей касательной позволяет однозначно зафиксировать составы сосуществующих в равновесии фаз x^L_B и x^S_B .

Установленное геометрическое условие равновесия, широко используется на практике при установлении возможных видов равновесия в двухкомпонентных системах.

Проекция отрезка общей касательной, заключенной между концентрациями равновесных фаз на соответствующую изотерму диаграммы Т – x_i является коннодой, т. е. прямой соединяющей фигуративные точки с координатами, характеризующими сосуществующие в равновесии при данных условиях фазы.

На рис. 1. 4 представлена принципиальная схема установления фиксированного положения координат фигуративных точек, соответствующих равновесно сосуществующим фазам в двухкомпонентной двухфазной системе при температуре Т₁. Обе фазы представляют собой неограниченные растворы компонентов А и В друг в друге, например, твердый раствор (S) и жидкий раствор (L).

Для того чтобы построить диаграмму состояния Т – x_i термодинамическим методом, необходимо получить серию кривых G_{p, T}=f(x_i) для различных температур. При этом напомним, что:

1. Чем выше температура, тем концентрационная зависимость свободной энергии Гиббса геометрически располагается ниже. Это следует из того, что температурная зависимость свободной энергииГиббса при увеличении температуры уменьшается.

2. При данной температуре ( р –const) устойчивой является фаза, имеющая более низкое значение изобарно-изотермического потенциала ( G_{p, T} ).

 

Рис. 1. 4. Принципиальная схема установления состава равновесных фаз в двухкомпонентной двухфазной системе

Перенося составы равновесных фаз при разных температурах на диаграмму в координатах состав − температура, можно построить диаграмму состояния двойной системы. Таким образом, метод расчета концентрационных зависимостей свободной энергии Гиббса позволяет теоретически обосновать разные варианты фазовых равновесий и построить соответствующие им диаграммы состояния. Отметим, что для получения надежных расчетов необходимо иметь информацию о взаимодействии компонентов во всех фазах данной термодинамической системы.

 

Эти рассуждения могут быть распространены на любые другие виды фазовых равновесий, например, между жидким раствором и газовой смесью. Для конденсированных систем, помимо важнейшего равновесия между твердой и жидкой фазами возможно существование равновесия между двумя жидкими фазами либо между двумя твердыми фазами в случае разрыва растворимости. Установление фиксированного положения координат равновесных фаз на диаграмме Т – х остается тем же самым, что и описано выше (рис. 1. 4).

На рис. 1. 5 схематически показано, как фиксируются координаты равновесных растворов a₁ и a₂, которые могут быть соответственно жидкими фазами или твердыми. В интервале концентраций от х_В1 до х_В2 растворы не устойчивы, т. е. происходит расслаивание и на кривой зависимости свободной энергии Гиббса появляется максимум. И в данном случае основной прием определения составов равновесных фаз при Т₁ сводится к проведению общей касательной

 

Рис. 1. 5. Принципиальная схема установления состава равновесных фаз при наличии распада твердого раствора или расслоения жидкого раствора.

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: