2.1.1.Определение состава равновесных фаз по диаграмме состояния

2. 1. 1. Определение состава равновесных фаз по диаграмме состояния

Чтобы определить состав однофазной системы (раствора) при любой температуре, достаточно опустить перпендикуляр из фигуративной точки на ось концентраций.

Данная концентрационная шкала позволяет определить содержание одновременно обоих компонентов. Если концентрация системы задается по компоненту В , как х_В, то концентрация компонента А определится: х_А=1–х_В.

Если система находится в двухфазной области, то для определения состава и количества каждой фазы пользуются коннодой – универсальным инструментом при исследовании диаграмм состояния.

Коннодой называется отрезок изотермы (т. к. равновесные фазы находятся при одинаковой температуре) или изобары, проведенный в двухфазной области до пересечения с линиями, ограничивающими эту область. Концы конноды (горизонтального отрезка), спроецированные на ось концентраций, указывают составы сосуществующих в равновесии (сопряженных) фаз.

Для рассматриваемой системы коннода проводится параллельно оси составов до пересечения с линиями, ограничивающими фазовое поле. Состав насыщенного жидкого раствора определяется пересечением с линией жидкости, состав равновесного с ним пара – пересечением с линией пара.

 

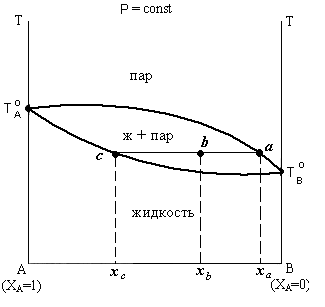
Рис 2. 4. Диаграмма состояния жидкость-пар

 

Например, система, отмеченная на диаграмме (рис. 2. 4. ) фигуративной точкой b и имеющая суммарный состав х_b, состоит из двух фаз. Проводим через эту точку конноду aс до пересечения с линиями жидкости и пара и получаем соответственно точку a, отвечающую пару состава х_а и точку с, отвечающую жидкости состава x_c.

Состав фаз определяем проекцией точек фаз на ось концентраций.

Необходимо отметить, что любая фигуративная точка на данной конноде имеет одинаковый состав равновесных фаз, но количество их будет различным.

2. 1. 2. Определение количественных соотношений

между равновесными фазами

С помощью диаграмм состояния можно определить не только составы равновесных фаз, но и их количества. Для этого используется правило рычага.

На рис. 2. 4. отрезок аb , примыкающий к составу пара пропорционален количеству жидкости, а отрезок bс, примыкающий к составу жидкости пропорционален количеству пара.

Для вывода правила рычага, составим уравнение материального баланса в системе, например для компонента В.

Пусть n_ж и n_пар - количества (моли) жидкой и парообразной фаз, а количество всей смеси n_b складывается из количеств жидкости и пара: n_b = n_ж + n_пар.

Если х_b - суммарная молярная долякомпонента В во всей системе, а х_а и x_с - молярная долякомпонента В в сосуществующих парообразной и жидкой равновесных фазах соответственно, тогда уравнение можно записать в виде:

nbxb = (nж + nпар ) xb = nжxс + nпар xа
или
(xb – xс)nж = (xа – xb)nпар ,

откуда можно выразить правило рычага:

(2. 2)

т. е. фигуративная точка, отвечающая суммарному составу системы ( b ), делит конноду, соединяющую фигуративные точки равновесных фаз ( а и с ), на части, обратно пропорциональные количеству этих фаз.

Вид математической записи “правила рычага” формально совпадает с аналогичной закономерностью в механике, если отрезок ac отож-дествить с рычагом, с опорой в точке b, а количество фаз n_ж и n_пар – с грузами на концах рычага.

Это правило еще называют правилом отрезков. Оно справедливо и для других видов диаграмм состояния и для других способов выражения концентрации.

Если состав равновесных фаз задан массовыми (молярными) процентами или массовыми (молярными) долями, то правило рычага позволяет найти соотношение между массами (числом молей) равновесных фаз.

 

2. 2. Давление насыщенного пара в реальных системах

В реальных системах наблюдается отклонение от линейной зависимости давления насыщенного пара от состава раствора.

Отклонение кривых “давление пара − состав” от линейной зависимости в сторону больших значений принято называть положительными, а в сторону меньших значений − отрицательными.

PоВ

Рис 2. 6. Зависимость общего давления пара Р и парциальных давлений PA, PB от состава раствора в системах с отрицательным отклонением от закона Рауля

Рис 2. 5. Зависимость общего давления пара P и парциальных давлений PA, PB от состава раствора в системах с положительным отклонением от закона Рауля

На рис. 2. 5. и рис. 2. 6. штрихами показана линейная зависимость давления насыщенного пара от состава раствора для идеальных растворов.

Для реальных растворов отклонения от идеальности обусловлены как физическими, так и химическими причинами: поляризация молекул, дипольное взаимодействие, водородные связи, ассоциация молекул, диссоциация ассоциатов молекул, комплексообразование и др.

Растворы, обладающие положительными отклонениями от закона Рауля (рис. 2. 5. ), образуются из чистых компонентов, в которых связи однотипных молекул A− A и B− B сильнее связи A− B.

FA− A > FA− B < FB− B

 

Тогда молекулам каждого компонента предпочтительнее связываться с себе подобными, чем с молекулами другого компонента. Положительные отклонения связаны с большими различиями в дипольных моментах обоих компонентов, высокой полярностью и склонностью чистых жидкостей к ассоциации. При образовании растворов, связи в одноименных ассоциатах, как правило, ослабевают, что способствует увеличению летучести компонентов.

Такие растворы образуются с поглощением тепла ( Δ H. >. 0 ), которое затрачивается на разрушение ассоциатов молекул исходных компонентов и увеличения объема ( Δ V. >. 0 ).

Растворы, обладающие отрицательными отклонениями от закона Рауля (рис. 2. 6. ), образуются из чистых компонентов, в которых связи одноименных молекул A− A и B− B менее прочные, чем разноименных.

FA− A < FA− B > FB− B

Такие компоненты склонны к образованию разноименных ассоциатов по типу химических соединений или образованию сольватных оболочек. Вследствие этого, теплота испарения компонентов из раствора оказывается большей, чем чистых компонентов.

Такие растворы образуются с выделением тепла ( Δ H. <. 0 ) и уменьшением объема ( Δ V. <. 0 ).

 

Вследствие отклонений от закона Рауля, выведенные для идеальных растворов уравнения непригодны для описания свойств реальных растворов. Для сохранения термодинамической зависимости свойств идеальных растворов в реальных системах используем величину термодинамической активности компонента − a_i.

В термодинамике реальных растворов активность заняла такое же место, какое в термодинамике идеальных растворов концентрация. Активность иногда называют эффективной или действующей концентрацией, она не вскрывает причин отклонения от идеальности, учитывая всю неидеальность раствора суммарно.

Термодинамическая активность компонента a_i, подставляемая в уравнения, выведенные для идеальных растворов, вместо концентрации делает их пригодными для расчета зависимостей реальных систем.

Закон Рауля для реальных растворов имеет вид:

(2. 3)

где:  и ─ давление насыщенного пара растворителя над раствором и растворителем соответственно;

─ термодинамическая активность растворителя

(2. 4)

где:  ─ коэффициент активности, который определяет отклонение реального раствора от идеального;

x_А ─ мольная доля растворителя

В идеальных растворах: a_i = x_i; γ _i = 1

В реальных растворах с положительными отклонениями от закона Рауля ─ a_i > x_i; γ _i > 1.

В растворах с отрицательными отклонениями от закона Рауля─ a_i < x_i; γ _i < 1.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: