 |
Теоретико-множественная интерпретация операций над событиями.
|
|
|
|
Пояснительная записка
Задачник по разделу «Теория вероятностей» (далее задачник) предназначен для обучающихся по специальностям: 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта», 13.02.11 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)», 15.02.08 «Технология машиностроения», 19.02.10 «Технология продукции общественного питания, а также для обучающихся по профессии 15.01.05 Сварщик (ручной и частично механизированной сварки (наплавки))».
Данный задачник применяется на занятиях по дисциплинам «ЕН.01 Математика» и «ОУД.07 Математика: алгебра и начала математического анализа, геометрия», а также предназначен для выполнения самостоятельной работы обучающихся по указанным дисциплинам.
Задачник по разделу «Теория вероятностей» разработан на основе Государственного образовательного стандарта среднего профессионального образования, утвержденного Министерством образования и науки Российской Федерации. В содержание задачника включены следующие темы: основные понятия теории вероятностей, действия с вероятностями, формула полной вероятности, формула Байеса, повторение испытаний, дискретные и непрерывные случайные величины, их числовые характеристики. К этому задачнику разработан курс лекций «Теория вероятностей».
Перед преподавателем, ведущим занятия по теории вероятностей, возникает дилемма: с одной стороны, необходимо ознакомить обучающихся с основными идеями теории предмета, с другой – временные рамки не позволяют сделать это на строгом математическом уровне.
Задачник рекомендуется для обучающихся профессиональных образовательных организаций:
|
|
|
1. Это не просто задачник, а еще самоучитель – по нему можно научиться решать задачи даже без преподавателя;
2. Задачник поможет подготовиться не только к зачету, но и к экзамену – обучающийся найдет в ней не только необходимые определения и теоремы по каждой теме (и все это кратко, без утомительных комментариев), но и типичные задачи, которые даются на экзамене;
3. Обучающийся найдет здесь задачи любого уровня сложности – от простых до таких, которые удовлетворят даже самых одарённых в группе;
4. Прочитав подробно разобранные примеры, обучающийся без проблем разберется с любым типом задач.
Структура этого курса уникальна тем, что данный задачник может одновременно играть роль учебника, задачника и справочника. Каждый параграф – это отдельная тема. В начале параграфа приводятся необходимые теоретические пояснения, включающие важнейшие определения и теоремы. Затем идет блок задач на эту тему, по объему и структуре соответствующий стандартному практикуму по теории вероятностей: сначала подробно разбираются 1-2 типовые задачи на тот или иной прием, после чего предлагается несколько аналогичных задач на его закрепление. А так же включены задачи повышенной сложности, обычно предлагаемые на экзаменах (зачетах) по дисциплинам «ЕН.01 Математика» и «ОУД.07 Математика: алгебра и начала математического анализа, геометрия».
В сборнике около 200 задач, и практически ко всем из них даны ответы или подробные решения и указания. Ответы ко всем задачам помещены в конце задачника.
Также в конце задачника приводится список литературы для углубленного изучения отдельных тем. Там же оформлен справочный материал – таблицы в виде приложений.
В данном задачнике большинство задач среднего уровня сложности, но есть и повышенного уровня. Лишь совсем немногие задачи требуют знания курса математического анализа, но и в этих случаях неподготовленный читатель все равно может понять постановку задачи, решение и ответ.
|
|
|
 Случайные события. Действия над событиями.
Случайные события. Действия над событиями.
Под испытанием (опытом) будем понимать процесс, включающий в себя определенные условия и приводящий к одному из нескольких возможных исходов. Стрельба по мишени, бросание монеты, вынимание шаров из урны – все это примеры опытов.
Событие – это результат опыта. События будем обозначать заглавными латинскими буквами А, В, С.
Единичный, отдельный исход опыта называется элементарным событием.
Событие называется достоверным, если оно обязательно произойдет в данном опыте. Достоверные события условимся обозначать буквой Ω.
Событие называется невозможным, если оно не может произойти в данном опыте. Невозможные события условимся обозначать символом  .
.
Событие называется случайным, если оно может произойти в данном опыте, а может и не произойти.
Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого.
Два события называются несовместными в данном опыте, если появление одного из них исключает появление другого.
События называются единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет (или одно, или два, или …, или все события из рассматриваемой совокупности событий произойдут).
События называются равновозможными, если нет оснований считать, что одно из них происходит чаще других.
Два единственно возможных и несовместных события называются противоположными.
Совокупность всех единственно возможных и несовместных событий называется полной группой событий.
Противоположные события – это полная группа из двух событий. Одно из противоположных событий обозначается А, другое  .
.
Введем основные операции над событиями; они полностью соответствуют основным операциям над множествами.
Если при всяком испытании, при котором происходит событие А, происходит событие В, то событие А называется частным случаем события В. Говорят также, что А влечет за собой В, и пишут: А  В (A вложено в В) или В
В (A вложено в В) или В  А.
А.
Если А влечет за собой В, а В влечет за собой А, то эти события равносильны, так как они вместе наступают или вместе не наступают.
|
|
|
Из того, что А  В и В
В и В  А следует А=В.
А следует А=В.
Произведением (пересечением) АВ (А  В) событий А и В называется событие, состоящее в совместном наступлении обоих событий, т.е. и А и В одновременно.
В) событий А и В называется событие, состоящее в совместном наступлении обоих событий, т.е. и А и В одновременно.
Суммой (объединением) А+В (А  В) событий А и В называется событие, состоящее в наступлении или события А, или события В (хотя бы одного из событий, по крайне мере одного из них).
В) событий А и В называется событие, состоящее в наступлении или события А, или события В (хотя бы одного из событий, по крайне мере одного из них).
Противоположным событию А называется событие  ,которое происходит тогда и только тогда, когда не происходит событие А.
,которое происходит тогда и только тогда, когда не происходит событие А.
Разностью (дополнением) А-В (А/В) событий А и В называется событие, происходящие тогда и только тогда, когда происходит событие А,но не происходит событие В.
Операции над событиями обладают следующими свойствами:
1. A + B = B + A, A  B = B
B = B  A – переместительный закон;
A – переместительный закон;
2. (A + B)  С=А
С=А  С+В
С+В  С – распределительный закон;
С – распределительный закон;
3. (А+В)+С=А+(В+С), (А  В)
В)  С=А
С=А  (В
(В  С)
С)  сочетательный закон;
сочетательный закон;
4. А+А=А, А  А=А;
А=А;
5. А+Ω=Ω, А  Ω= A;
Ω= A;
6. А +  = Ω, А
= Ω, А  =
=  ;
;
7.  =Ω,
=Ω,  =
=  ,
,  = А;
= А;
8. А-В=А  ;
;
9.  =
=  ,
,  =
=  (законы де Морга).
(законы де Морга).
Пример 1: доказать формулу А+В=А+  B
B
А+В=(А+В)  Ω =А
Ω =А  Ω+ B
Ω+ B  Ω =А
Ω =А  Ω+ B
Ω+ B  (A +
(A +  =А
=А  Ω+(A +
Ω+(A +  B =А
B =А  Ω+ A
Ω+ A  B +
B +  =(Ω + B)
=(Ω + B)  A +
A +  B ==Ω
B ==Ω  A +
A +  = А+
= А+  B.
B.
ч.т.д.
Теоретико-множественная интерпретация операций над событиями.
Множество Ω=  всех возможных взаимоисключающих исходов данного опыта называется пространством элементарных событий (ПЭС), а сами исходы ω
всех возможных взаимоисключающих исходов данного опыта называется пространством элементарных событий (ПЭС), а сами исходы ω  элементарными событиями (или «элементами», «точками»).
элементарными событиями (или «элементами», «точками»).
Случайным событием А (или просто событием А) называется любое подмножество множества Ω, если Ω конечно или счетно(т.е. элементы этого множества можно пронумеровать с помощью множества натуральных чисел): А  Ω.
Ω.
Элементарные события, входящие в подмножество А пространства Ω, называются благоприятствующими событию А.
Множество Ω называется достоверным событием. Ему благоприятствует любое элементарное событие; в результате опыта оно обязательно произойдет.
Пустое множество  называется невозможным событием; в результате опыта оно произойти не может.
называется невозможным событием; в результате опыта оно произойти не может.
Пример2: Опыт: один раз бросают игральную кость.
В этом случае ПЭС таково:  или
или  , где
, где  - элементарное событие, состоящее в выпадении грани с i очками (i =
- элементарное событие, состоящее в выпадении грани с i очками (i =  ). В данном случае Ω конечно.
). В данном случае Ω конечно.
|
|
|
Примером события А является, например, выпадение нечетного числа очков; очевидно, что А =  ; событию А благоприятствуют элементарные события
; событию А благоприятствуют элементарные события  .
.
Однако если нас интересует только факт выпадения четного числа очков, то ПЭС можно построить иначе: Ω=  , где
, где  – выпадение четного числа очков,
– выпадение четного числа очков,  – нечетного.
– нечетного.
Над событиями можно проводить все операции, выполняемые для множеств.
Суммой (объединением) двухсобытий А  и В
и В  (обозначается А+В (А
(обозначается А+В (А  В)) – это множество, которое содержит элементы, принадлежащие хотя бы одному из событий А и В.
В)) – это множество, которое содержит элементы, принадлежащие хотя бы одному из событий А и В.
Произведением (пересечением) двухсобытий А  и В
и В  (обозначается АВ (А
(обозначается АВ (А  В)) - это множество, которое содержит элементы, общие для событий А и В.
В)) - это множество, которое содержит элементы, общие для событий А и В.
Разностью (дополнением) событий А  и В
и В  (обозначается А-В (А/В)) - это множество, которое содержит элементы события А, не принадлежащие событию В.
(обозначается А-В (А/В)) - это множество, которое содержит элементы события А, не принадлежащие событию В.
Противоположным событию А  называется событие
называется событие  . (
. (  называют также дополнением множества А.
называют также дополнением множества А.
Событие А влечет событие В (обозначается A ⊆ B), если каждый элемент события А содержится в В.
По определению:  для любого А.
для любого А.
События А и В называются несовместными, если их произведение есть невозможное событие, т.е. А  В=
В=  .
.
Несколько событий  образуют полную группу несовместных событий, если их сумма представляет все ПЭС, а сами события несовместны, т.е.
образуют полную группу несовместных событий, если их сумма представляет все ПЭС, а сами события несовместны, т.е.  =
=  (i
(i  j) и
j) и

Полную группу образуют, например, события А и  (А +
(А +  = Ω, А
= Ω, А  =
=  ).
).
Упражнения:
1. В урне находятся 12 пронумерованных шаров. Опыт состоит в извлечении одного шара из урны. Требуется:
1) составить пространство элементарных событий для данного опыта;
2) указать элементарные события (исходы), благоприятствующие событиям:
А =  , В =
, В =  , C =
, C =  , D =
, D =  ;
;
3) пояснить, что означают события  ;
;
4) указать, какие из пар событий A, B, C, D совместны, а какие нет;
5) указать, какие из пар событий A, B, C, D образуют полную группу, а какие нет;
6) привести примеры невозможного и достоверного событий;
7) привести пример другого пространства элементарных событий в данном опыте.
2. Указать пространства элементарны событий для следующих опытов:
а) подбрасывание двух игральных костей;
б) стрельба по мишени до первого попадания;
в) наблюдение за временем безотказной работы прибора.
3. Какие из следующих пар событий являются несовместными, совместными:
а) А – выход из строя телевизора, работающего в гостиной,
В  выход из строя телевизора, работающего кухне;
выход из строя телевизора, работающего кухне;
б) С – попадание при одном выстреле, D  промах;
промах;
в) Е – выпадение герба при бросании монеты, F  выпадение решки;
выпадение решки;
г) G – хотя бы одно попадание при двух выстрелах, H – два попадания?
|
|
|
4. Образуют ли полную группу следующие события:
а)  – попадание при одном выстреле,
– попадание при одном выстреле, 
 промах;
промах;
б)  – хотя бы одно попадание при двух выстрелах,
– хотя бы одно попадание при двух выстрелах,  – два попадания;
– два попадания;
в)  – ни одного попадания при трех выстрелах,
– ни одного попадания при трех выстрелах,
 – одно попадание,
– одно попадание,  – два попадания,
– два попадания,  – три попадания;
– три попадания;
г)  – покупатель купит товар хотя бы в одном из трех магазинов,
– покупатель купит товар хотя бы в одном из трех магазинов,
 – не купит ни в одном магазине?
– не купит ни в одном магазине?
5. Каждый из двух стрелков производит по одному выстрелу в мишень. Пусть событие А - первый стрелок попал в цель, событие В – второй стрелок попал в цель. Что означают события: а)  ; б)
; б)  ; в)
; в)  .
.
6. Три студента независимо друг от друга решают одну и ту же задачу. Пусть событие  – первый студент решил задачу,
– первый студент решил задачу, 
 второй студент решил задачу,
второй студент решил задачу,  – третий студент решил задачу. Выразить через события
– третий студент решил задачу. Выразить через события  ,
,  следующие события:
следующие события:
1) A – все студенты решили задачу;
2) B – задачу решил только первый студент;
3) C – задачу решил хотя бы один студент;
4) D – задачу решил только один студент.
7. Из корзины, содержащей красные, желтые и белые розы, выбирается один цветок. Пусть событие A – выбрана красная роза, событие B – выбрана желтая роза, событие C – выбрана белая роза. Что означают события:
а)  , б)
, б)  , в)
, в)  , г)
, г)  , д)
, д)  , е)
, е)  ?
?
8. Пусть  – три произвольных события. Выразить через
– три произвольных события. Выразить через  и их отрицания следующие события:
и их отрицания следующие события:
а) произошло только событие C;
б) произошли все три события;
в) произошло по крайне мере одно из этих событий;
г) произошло по крайне мере два события;
д) произошло только два события;
е) ни одно событие не произошло;
ж) произошло не более двух событий.
9. Упростить выражения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
10. Доказать справедливость законов де Моргана:
а) 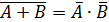 ; б)
; б)  .
.
|
|
|


