 |
Показательный закон распределения.
|
|
|
|
Непрерывная случайная величина X имеет показательный (экспоненциальный) законом распределения, если ее плотность вероятности имеет вид
 (1) где λ
(1) где λ 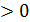 – параметр распределения.
– параметр распределения.
График плотности  приведен на рисунке 1:
приведен на рисунке 1:
 рис.1
рис.1
Показательное распределение определяется одним параметром λ. Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большого числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т.д. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.
Функция распределения показательного закона имеет вид
 (2)
(2)
График 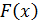 выглядит:
выглядит:
 рис.2
рис.2
Математическое ожидание и дисперсия показательного распределения:
 ,
, 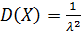 ,
,  =
=  .
.
Вероятность попадания в интервал  непрерывной случайной величины Х, которая распределена по показательному закону, заданному функцией распределения (2):
непрерывной случайной величины Х, которая распределена по показательному закону, заданному функцией распределения (2):  (3)
(3)
Значения функции е находят по таблице.
Пример 1: Непрерывная случайная величина Х распределена по показательному закону 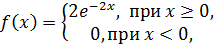 Найти вероятность того, что в результате испытания Х попадает в интервал (0,3; 1).
Найти вероятность того, что в результате испытания Х попадает в интервал (0,3; 1).
Решение: По условию, λ=2. Воспользуемся формулой (3).

Ответ: 0,41
Пример 2: Случайная величина Т - время работы радиолампы имеет показательное распределение. Найти вероятность того, что лампа проработает не менее 800 часов, если среднее время работы радиолампы 400 часов.
Решение: Математическое ожидание М(Т) =400, значит  . Искомая вероятность
. Искомая вероятность

|
|
|
Ответ: 
Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания (ТМО), в физике, в теории надежности. Оно используется для описания распределения случайной величины вида: длительность работы прибора до первого отказа, длительность времени обслуживания в системе массового обслуживания и т.д.
Рассмотрим: непрерывную случайную величину Т - длительность безотказной работы прибора. Функция распределения случайной величины Т, т.е.  , определяет вероятность отказа за время длительностью t. И, значит, вероятность безотказной работы за время t равна
, определяет вероятность отказа за время длительностью t. И, значит, вероятность безотказной работы за время t равна  . Функция
. Функция  называется функцией надежности.
называется функцией надежности.
Случайная величина Т часто имеет показательное распределение. Ее функция распределения имеет вид  . В этом случае функция надежности имеет вид
. В этом случае функция надежности имеет вид  , т.е.
, т.е. 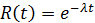 , где λ – интенсивность отказов, т.е. среднее число отказов в единицу времени.
, где λ – интенсивность отказов, т.е. среднее число отказов в единицу времени.
Показательный закон - единственный из законов распределения, который обладает свойством «отсутствия последствия», т.е. если промежуток времени Т уже длился некоторое время  , то показательный закон распределения остается таким же и для оставшейся части
, то показательный закон распределения остается таким же и для оставшейся части  промежутка.
промежутка.
Упражнения:
1. Время T выхода из строя радиостанции подчинено показательному закону распределения с плотностью  Найти: функцию распределения
Найти: функцию распределения  ; математическое ожидание и дисперсию случайной величины T; вероятность того, чторадиостанция сохранит работоспособность от 1 до 5 часов работы.
; математическое ожидание и дисперсию случайной величины T; вероятность того, чторадиостанция сохранит работоспособность от 1 до 5 часов работы.
2. Случайная величина X имеет показательное распределение 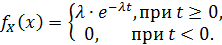 Найти функцию распределения
Найти функцию распределения  ; вероятность
; вероятность  .
.
3. Случайная величина X распределена по показательному закону с параметром λ=0,4. Найти дифференциальную и интегральную функции распределения, среднее квадратическое отклонение  , а также вероятность попадания значений случайной величины X в интервал
, а также вероятность попадания значений случайной величины X в интервал  .
.
4. Случайная величина X, которая равна длительности работы элемента, имеет плотность распределения  Найти: среднее время работы элемента; вероятность того, что элемент проработает не менее 400 часов.
Найти: среднее время работы элемента; вероятность того, что элемент проработает не менее 400 часов.
|
|
|
5. Средняя продолжительность телефонного разговора равна 3 минутам. Найти вероятность того, что произвольный телефонный разговор будет продолжаться не более 9 минут, считая, что время разговора является случайной величиной X, распределенной по показательному закону.
Нормальное распределение.
Нормальный закон («закон Гаусса») играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Нормальный закон наиболее часто встречается на практике.
Непрерывная случайная величина Х распределена по нормальному закону с параметрами a и 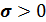 , если ее плотность распределения имеет вид
, если ее плотность распределения имеет вид
 (1),
(1),  .
.
Случайная величина Х имеет нормальное (или гауссовское) распределение с параметрами a и 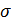 , сокращенно записывается так:
, сокращенно записывается так:  .
.
Функция распределения

непрерывной случайной величины X  имеет вид:
имеет вид:

Если  , то нормальное распределение с такими параметрами называется стандартным. Плотность стандартной случайной величины имеет вид
, то нормальное распределение с такими параметрами называется стандартным. Плотность стандартной случайной величины имеет вид

Функция распределения случайной величины Х  имеет вид
имеет вид

и называется функцией Лапласа. Она связана с нормированной функцией Лапласа  равенством
равенством  .
.
Установим смысл параметров  нормального распределения Х
нормального распределения Х  :
:  и
и  ,
, 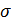 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Можно показать, что для случайной величины Х  :
:  ,
, 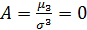 ,
,  .
.
График плотности распределения вероятности нормального закона - кривую распределения, называемую нормальной кривой (кривой Гаусса).
 рис.1
рис.1
Нормальному закону подчиняются ошибки измерений, величины износа деталей в механизмах, рост человека, ошибки стрельбы, вес клубней картофеля, величина шума в радиоприемном устройстве, колебания курса акций и т.д.
Вероятность попадания случайной величины Х  на заданный участок
на заданный участок  :
:  . (3)
. (3)
Через функцию Лапласа 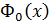 выражается и функция распределения
выражается и функция распределения  нормально распределенной случайной величины Х.
нормально распределенной случайной величины Х.
 (4)
(4)
На практике часто приходиться вычислять вероятность попадания нормально распределенной случайной величины в интервал, симметричный относительно центра рассеяния а. Пусть таким интервалом будет  длины 2 l. Тогда
длины 2 l. Тогда
|
|
|

т.е.
 . (5)
. (5)
Полагая в равенстве (5)  , получим
, получим  По таблице значений для
По таблице значений для 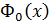 находим:
находим:  . Следовательно,
. Следовательно,  , т.е. отклонение случайной величины Х от своего математического ожидания меньше, чем 3
, т.е. отклонение случайной величины Х от своего математического ожидания меньше, чем 3 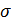 – почти достоверное событие.
– почти достоверное событие.
Вывод: практически достоверно, что случайная величина Х  принимает свои значения в промежутке
принимает свои значения в промежутке  . Это утверждение называется «правилом трех сигм».
. Это утверждение называется «правилом трех сигм».
Пример 1: При измерении детали получается случайные ошибки, подчиненные нормальному закону с параметром 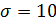 мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.
мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.
Решение: По формуле (6) находим:
 .
.
Вероятность того, что эта ошибка (погрешность) превышает 2 мм в одном опыте (измерении), равна
 .
.
По теории умножения вероятность того, что во всех трех опытах ошибка измерения превышает 2 мм, равна  . Следовательно, искомая вероятность равна
. Следовательно, искомая вероятность равна  1-0,5958=0,4042.
1-0,5958=0,4042.
Ответ: 0,4042
Упражнения:
1. Определить закон распределения случайной величины X, если ее плотность вероятности имеет вид
 .
.
Найти: а)  ; б)
; б)  ; в) значение коэффициента A; г)
; в) значение коэффициента A; г)  ; д)
; д)  .
.
2. Случайные ошибки измерения детали подчинены нормальному закону с параметрами  . Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
3. Пусть  . Найти вероятность того, что при трех независимых испытаниях случайная величина X хотя бы в одном из них X примет значение в интервале
. Найти вероятность того, что при трех независимых испытаниях случайная величина X хотя бы в одном из них X примет значение в интервале  .
.
4. Плотность вероятностей случайной величины X имеет вид
 .
.
Найти: а) значение коэффициента C; б)  ; в)
; в) 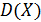 ; г)
; г) 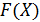 ; д)
; д)  .
.
5. Известно, что  ,
, 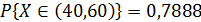 . Найти D (X).
. Найти D (X).
6. Рост взрослых мужчин является случайной величиной X, распределенной по нормальному закону:  . Найти плотность вероятности, функцию распределения этой случайной величины; вероятность того, что ни один из 3 наудачу выбранных мужчин не будет иметь рост менее 180см.
. Найти плотность вероятности, функцию распределения этой случайной величины; вероятность того, что ни один из 3 наудачу выбранных мужчин не будет иметь рост менее 180см.
Приложения
Приложение 1.
Таблица функции  (кривая вероятностей)
(кривая вероятностей)
|
|
|

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3725 | 0,3712 | 0,3697 |
| 0,4 | 0,3683 | 0,3668 | 0,3653 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3521 | 0,3503 | 0,345 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1,0 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,202 | 0,1989 | 01965 |
| 1,2 | 0,1942 | 0,14919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,126 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 2,0 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0355 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,026 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 |
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
| 4,0 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 |
| 4,1 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 |
| 4,2 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
Приложение 2.
Таблица функции  (функция Лапласа)
(функция Лапласа)

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0,0 | 0,00000 | 0,00399 | 0,00798 | 0,01197 | 0,01595 | 0,01994 | 0,02392 | 0,02790 | 0,03188 | 0,03586 | ||
| 0,1 | 0,03983 | 0,04380 | 0,04776 | 0,05172 | 0,05567 | 0,05962 | 0,06356 | 0,06749 | 0,07142 | 0,07535 | ||
| 0,2 | 0,07926 | 0,08317 | 0,08706 | 0,09095 | 0,09483 | 0,09871 | 0,10257 | 0,10642 | 0,11026 | 0,11409 | ||
| 0,3 | 0,11791 | 0,12172 | 0,12552 | 0,12930 | 0,13307 | 0,13683 | 0,14058 | 0,14431 | 0,14803 | 0,15173 | ||
| 0,4 | 0,15542 | 0,15910 | 0,16276 | 0,16640 | 0,17003 | 0,12364 | 0,17724 | 0,18082 | 0,18439 | 0,18793 | ||
| 0,5 | 0,19146 | 0,19497 | 0,19847 | 0,20194 | 0,20540 | 0,20884 | 0,21226 | 0,21566 | 0,21904 | 0,22240 | ||
| 0,6 | 0,22575 | 0,22907 | 0,23237 | 0,23565 | 0,23891 | 0,24215 | 0,24537 | 0,24857 | 0,25175 | 0,25490 | ||
| 0,7 | 0,25804 | 0,26115 | 0,26424 | 0,26730 | 0,27035 | 0,27337 | 0,27637 | 0,27935 | 0,28230 | 0,28524 | ||
| 0,8 | 0,28814 | 0,29103 | 0,29389 | 0,29673 | 0,29955 | 0,30234 | 0,30511 | 0,30785 | 0,31057 | 0,31327 | ||
| 0,9 | 0,31594 | 0,31859 | 0,32121 | 0,32381 | 0,32639 | 0,32894 | 0,33147 | 0,33398 | 0,33646 | 0,33891 | ||
| 1,0 | 0,34134 | 0,34375 | 0,34614 | 0,34849 | 0,35083 | 0,35314 | 0,35543 | 0,35769 | 0,35993 | 0,36214 | ||
| 1,1 | 0,36433 | 0,36650 | 0,36864 | 0,37076 | 0,37286 | 0,37493 | 0,37698 | 0,37900 | 0,38100 | 0,38298 | ||
| 1,2 | 0,38493 | 0,38686 | 0,38877 | 0,39065 | 0,39251 | 0,39435 | 0,39617 | 0,39796 | 0,39973 | 0,40147 | ||
| 1,3 | 0,40320 | 0,40490 | 0,40658 | 0,40824 | 0,40988 | 0,41149 | 0,41308 | 0,41466 | 0,41621 | 0,41774 | ||
| 1,4 | 0,41924 | 0,42073 | 0,42220 | 0,42364 | 0,42507 | 0,42647 | 0,42785 | 0,42922 | 0,43056 | 0,43189 | ||
| 1,5 | 0,43319 | 0,43448 | 0,43574 | 0,43699 | 0,43822 | 0,43943 | 0,44062 | 0,44179 | 0,44295 | 0,44408 | ||
| 1,6 | 0,44520 | 0,44630 | 0,44738 | 0,44845 | 0,44950 | 0,45053 | 0,45154 | 0,45254 | 0,45352 | 0,45449 | ||
| 1,7 | 0,45543 | 0,45637 | 0,45728 | 0,45818 | 0,45907 | 0,45994 | 0,46080 | 0,46164 | 0,46246 | 0,46327 | ||
| 1,8 | 0,46407 | 0,46485 | 0,46562 | 0,46638 | 0,46712 | 0,46784 | 0,46856 | 0,46926 | 0,46995 | 0,47062 | ||
| 1,9 | 0,47128 | 0,47193 | 0,47257 | 0,47320 | 0,47381 | 0,47441 | 0,47500 | 0,47558 | 0,47615 | 0,47670 | ||
| 2,0 | 0,47725 | 0,47778 | 0,47831 | 0,47882 | 0,47932 | 0,47982 | 0,48030 | 0,48077 | 0,48124 | 0,48169 | ||
| 2,1 | 048214 | 0,48257 | 0,48300 | 0,48341 | 0,48382 | 0,48422 | 0,4861 | 0,48500 | 0,48537 | 0,48574 | ||
| 2,2 | 0,48610 | 0,48645 | 0,48679 | 0,48713 | 0,48745 | 0,48778 | 0,48809 | 0,48840 | 0,48870 | 0,48899 | ||
| 2,3 | 0,48928 | 0,48956 | 0,48983 | 0,48010 | 0,49036 | 0,49061 | 0,49086 | 0,49111 | 0,49134 | 0,49158 | ||
| 2,4 | 0,49180 | 0,49202 | 0,49224 | 0,49245 | 0,49266 | 0,49286 | 0,49305 | 0,49324 | 0,49343 | 0,49361 | ||
| 2,5 | 0,49379 | 0,49396 | 0,49413 | 0,49430 | 0,49446 | 0,49461 | 0,49477 | 0,49492 | 0,49506 | 0,49520 | ||
| 2,6 | 0,49534 | 0,49547 | 0,49560 | 0,49573 | 0,49585 | 0,49598 | 0,49609 | 0,49621 | 0,49632 | 0,49643 | ||
| 2,7 | 0,49653 | 0,49664 | 0,49674 | 0,49683 | 0,49693 | 0,49702 | 0,49711 | 0,49720 | 0,49728 | 0,49736 | ||
| 2,8 | 0,49744 | 0,49752 | 0,49760 | 0,49767 | 0,49774 | 0,49781 | 0,49788 | 0,49795 | 0,49801 | 0,49807 | ||
| 2,9 | 0,49813 | 0,49819 | 0,49825 | 0,49831 | 0,49836 | 0,49841 | 0,49846 | 0,49851 | 0,49856 | 0,49861 | ||
| 3,0 | 0,49865 | 0,49869 | 0,49874 | 0,49878 | 0,49882 | 0,49886 | 0,49889 | 0,49893 | 0,49896 | 0,49900 | ||
| 3,1 | 0,49903 | 0,49906 | 0,49910 | 0,49913 | 0,49916 | 0,49918 | 0,49921 | 0,49924 | 0,49926 | 0,49929 | ||
| 3,2 | 0,49931 | 0,49934 | 0,49936 | 0,49938 | 0,49940 | 0,49942 | 0,49944 | 0,49946 | 0,49948 | 0,49950 | ||
| 3,3 | 0,49952 | 0,49953 | 0,49955 | 0,49957 | 0,49958 | 0,49960 | 0,49961 | 0,49962 | 0,49964 | 0,49965 | ||
| 3,4 | 0,49966 | 0,49968 | 0,49969 | 0,49970 | 0,49971 | 0,49972 | 0,49973 | 0,49974 | 0,49975 | 0,49976 | ||
| 3,5 | 0,49977 | 0,49978 | 0,49978 | 0,49979 | 0,49980 | 0,49981 | 04,9981 | 0,49982 | 0,49983 | 0,49983 | ||
| 3,6 | 0,49984 | 0,49985 | 0,49985 | 0,49986 | 0,49986 | 0,49987 | 0,49987 | 0,49988 | 0,49988 | 0,49989 | ||
| 3,7 | 0,49989 | 0,49990 | 0,49990 | 0,49990 | 0,49991 | 0,49991 | 0,49992 | 0,49992 | 0,49992 | 0,49992 | ||
| 3,8 | 0,49993 | 0,49993 | 0,49993 | 0,49994 | 0,49994 | 0,49994 | 0,49994 | 0,49995 | 0,49995 | 0,49995 | ||
| 3,9 | 0,49995 | 0,49995 | 0,49996 | 0,49996 | 0,49996 | 0,49996 | 0,49996 | 0,49996 | 0,49997 | 0,49997 | ||
| 4,0
| 0,499968 | |||||||||||
| 4,5 | 0,499997 | |||||||||||
| 5,0 | 0,4999997 | |||||||||||
Приложение 3.
Таблица значений функций Пуассона: 
| m | λ | 0, 1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| 0 | 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,4966 | 0,4493 | 0,4066 | |
| 1 | 0,0905 | 0,1638 | 0,2222 | 0,2681 | 0,3033 | 0,3293 | 0,3476 | 0,3596 | 0,3659 | |
| 2 | 0,0045 | 0,0164 | 0,0333 | 0,0536 | 0,0758 | 0,0988 | 0,1217 | 0,1438 | 0,1647 | |
| 3 | 0,0002 | 0,011 | 0,0033 | 0,072 | 0,0126 | 0,0198 | 0,0284 | 0,0383 | 0,0494 | |
| 4 | - | 0,0001 | 0,0003 | 0,0007 | 0,0016 | 0,0030 | 0,0050 | 0,0077 | 0,0111 | |
| 5 | - | - | - | 0,0001 | 0,0002 | 0,0004 | 0,0007 | 0,0012 | 0,0020 | |
| 6 | - | - | - | - | - | - | 0,0001 | 0,0002 | 0,0003 | |
| m | λ | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| 0 | 0,3679 | 0,1353 | 0,0498 | 0,0183 | 0,0067 | 0,0025 | 0,0009 | 0,0003 | 0,0001 | |
| 1 | 0,3679 | 0,2707 | 0,1494 | 0,0733 | 0,0337 | 0,0149 | 0,0064 | 0,0027 | 0,0011 | |
| 2 | 0,1839 | 0,2707 | 0,2240 | 0,1465 | 0,0842 | 0,0446 | 0,0223 | 0,0107 | 0,0050 | |
| 3 | 0,0613 | 0,1805 | 0,2240 | 0,1954 | 0,1404 | 0,0892 | 0,0521 | 0,0286 | 0,0150 | |
| 4 | 0,0153 | 0,0902 | 0,1680 | 0,1954 | 0,1755 | 0,1339 | 0,0912 | 0,0572 | 0,037 | |
| 5 | 0,0031 | 0,0361 | 0,1008 | 0,1563 | 0,1755 | 0,1606 | 0,1277 | 0,0916 | 0,0607 | |
| 6 | 0,0005 | 0,0120 | 0,0504 | 0,1042 | 0,1462 | 0,1606 | 0,1490 | 0,1221 | 0,0911 | |
| 7 | 0,0001 | 0,0034 | 0,0216 | 0,0595 | 0,1045 | 0,1377 | 0,1490 | 0,1396 | 0,1171 | |
| 8 | - | 0,0009 | 0,0081 | 0,0298 | 0,0655 | 0,1033 | 0,1304 | 0,1396 | 0,1318 | |
| 9 | - | 0,0002 | 0,0027 | 0,0132 | 0,0363 | 0,0689 | 0,1014 | 0,1241 | 0,1318 | |
| 10 | - | - | 0,0008 | 0,053 | 0,0181 | 0,0413 | 0,0710 | 0,0993 | 0,1186 | |
| 11 | - | - | 0,0002 | 0,0019 | 0,0082 | 0,0225 | 0,0452 | 0,0722 | 0,0970 | |
| 12 | - | - | 0,0001 | 0,0006 | 0,0034 | 0,0113 | 0,0264 | 0,0481 | 0,0728 | |
| 13 | - | - | - | 0,0002 | 0,0013 | 0,0052 | 0,0142 | 0,0296 | 0,0504 | |
| 14 | - | - | - | 0,0001 | 0,0005 | 0,0022 | 0,0071 | 0,0169 | 0,0324 | |
| 15 | - | - | - | - | 0,002 | 0,0009 | 0,0033 | 0,0090 | 0,0194 | |
| 16 | - | - | - | - | - | 0,003 | 0,0015 | 0,0045 | 0,0109 | |
| 17 | - | - | - | - | - | 0,001 | 0,0006 | 0,0021 | 0,0058 | |
| 18 | - | - | - | - | - | - | 0,0002 | 0,0009 | 0,0029 | |
| 19 | - | - | - | - | - | - | 0,0001 | 0,0004 | 0,0014 | |
| 20 | - | - | - | - | - | - | - | 0,0002 | 0,0006 | |
| 21 | - | - | - | - | - | - | - | 0,0001 | 0,0003 | |
| 22 | - | - | - | - | - | - | - | 0,0001 | ||
Ответы
|
|
|


