 |
Дискретные случайные величины.
|
|
|
|
Различают дискретные и непрерывные случайные величины.
Случайная величина, принимающая конечное или счетное множество значений, называется дискретной. (д.с.в.)
Дискретная случайная величина принимает отдельные изолированные друг от друга значения.
Например: 1. X – число очков, появляющихся при бросании игральной кости; 2. Y- число выстрелов до первого попадания в цель.
О непрерывных случайных величинах пойдет речь в следующем параграфе.
Законом распределения дискретной случайной величины называют соотношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины таблица состоит из двух строк и называется законом или рядом распределения дискретной случайной величиной X.
Первая строка таблицы содержит возможные значения случайной величины, а вторая – соответствующие вероятности. Если обозначить возможные числовые значения случайной величины X через  , а вероятности появления значения
, а вероятности появления значения 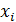 через
через  , то дискретная случайная величина полностью определяется таблицей:
, то дискретная случайная величина полностью определяется таблицей:
| x | 
| 
| … | 
| 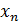
|
| p | 
| 
| … | 
| 
|
Значения  записываются в таблице, как правило, в порядке возрастания.
записываются в таблице, как правило, в порядке возрастания.
Приняв во внимание, что в каждом отдельном испытании случайная величина принимает только одно возможное значение случайной величины X, заключаем, что события X =  , X =
, X =  ,…, X =
,…, X = 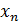 несовместны и образуют полную группу событий. Следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице:
несовместны и образуют полную группу событий. Следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице:
|
|
|

Табличный способ задания закона распределения используется только для дискретной случайной величины.
Закон распределения дискретной случайной величины можно задать графически, если на оси абсцисс отложить возможные значения случайной величины, а на оси ординат – вероятности этих значений. Ломанную, соединяющую последовательно точки ( ), (
), ( ),…,(
),…,( ) называют многоугольником (или полигоном) распределения.
) называют многоугольником (или полигоном) распределения.

Теперь можно дать более точное определение дискретной случайной величины.
Случайная величина X дискретна, если существует конечное или счетное множество чисел  таких, что P
таких, что P  =
=  (i=1,2,..) и
(i=1,2,..) и

Пример 1: В урне 8 шаров, из которых 5 белых, остальные - черные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке.
Решение: Случайная величина X – число белых шаров в выборке. Возможные значения:  =0,
=0,  =1,
=1,  =2,
=2,  =3.
=3.
Вероятности их соответственно будут  ,
, 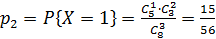 ,
,
 ,
,
 .
.
Закон распределения примет вид:
| X | 0 | 1 | 2 | 3 |
| p | 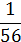
| 
| 
| 
|
Контроль
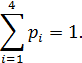
Функцией распределения дискретной случайной величины называют функцию 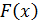 , определенную для каждого значения x вероятность того, что случайная величина X примет значение меньше, чем значение аргумента функции – x:
, определенную для каждого значения x вероятность того, что случайная величина X примет значение меньше, чем значение аргумента функции – x:
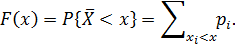
Вычисляя функцию распределения дискретной случайной величины для заданного аргумента, суммируют вероятности всех значений случайной величины, которые меньше аргумента функции распределения (лежат левее значения аргумента в ряду распределения).
Функция распределения дискретной случайной величины X есть разрывная функция, со скачками 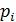 в точках
в точках 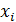 ,»непрерывная слева» (при подходе к точке разрыва слева функция
,»непрерывная слева» (при подходе к точке разрыва слева функция 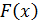 сохраняет значение). Ее график имеет ступенчатый вид.
сохраняет значение). Ее график имеет ступенчатый вид.
Пример 2: По условию примера 1 найти функцию распределения 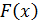 и построить ее график.
и построить ее график.
Решение: Будем задавать различные значения x и находить для них  :
:
1. Если  , то
, то  =0;
=0;
2. Если  , то
, то  =
=  ;
;
|
|
|
3. Если  , то
, то 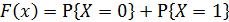 =
=  ;
;
4. Если  , то
, то  =
= 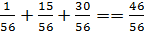 ;
;
5. Если 3  , то
, то  =
= 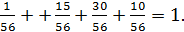
Итак, 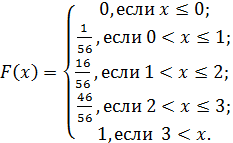
Строим график 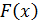 .
.

|
|
|


