 |
Биномиальный закон распределения.
|
|
|
|
Среди законов распределения дискретной случайной величины наиболее распространенным является биномиальное распределение, с которым мы уже встречались.
Пусть производится n независимых испытаний, в каждом из которых событие A может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p, а не появления - q =1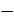 
p. Рассмотрим в качестве дискретной случайной величины X число появлений события A в этих испытаниях. Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности. Очевидно, что в результате n испытаний событие может не появиться вовсе, появиться один, два, три т.д. до n раз.
Вероятность каждого значения дискретной случайной величины можно найти по формуле Бернулли: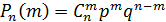 
(1), m =0,1,2,…, n, 
.Такой закон распределения называется биномиальным законом с параметрами 
и 
.
Формула (1) является аналитическим выражением искомого закона распределения. Закон назван «биномиальным» потому, что правую часть равенства (1) можно рассматривать как общий член разложения бинома Ньютона:
.
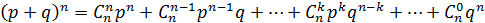Таким образом, первый член разложения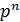 
определяет вероятность наступления рассматриваемого события n раз в n независимых опытах; второй член n 
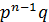определяет вероятность наступления события n -1 раз;…; последний член 
определяет вероятность того, что событие не появится ни разу.
Заметим, что сумма вероятностей
Если требуется вычислить вероятность «не менее m успехов в n независимых испытаниях», т.е. 
, то имеем
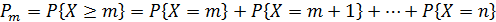(2).
Вероятность 
бывает удобно находить через вероятность противоположного события:
. (3)
Из формул (2) и (3) лучше, где меньше слагаемых.
Ряд распределения дискретной случайной величины X, распределенной по биномиальному закону, имеет вид:
|
|
|
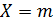
| 0 | 1 | 2 | … | m | … | n |
|
| 
| 
| … | 
| … |
|
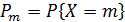
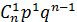
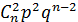
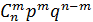
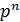
Контроль 
.
Функция распределения случайной величины X, распределенной по биномиальному закону, имеет вид: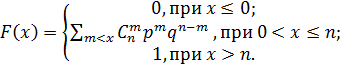 
Числовые характеристики биномиального распределения.
Математическое ожидание, среднее ожидаемое значение дискретной случайной величины: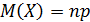 
(4), здесь n - количество испытаний, 
вероятность успеха в каждом испытании.
Дисперсия (квадрат отклонений значений случайной величины от математического ожидания) 
, где n - количество испытаний,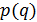 
- вероятность успеха (неудачи) в каждом опыте.
Среднее квадратическое отклонение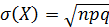 
.
Пример 1: Производится три независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны 0,9. Найт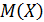и 
и 
, где X - число попаданий в цель.
Решение: Ряд распределения случайной величины X имеет биномиальное распределение.
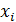
| 0 | 1 | 2 | 3 |
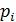
| 0,001 | 0,027 | 0,243 | 0,729 |
Здесь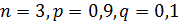 
. 
и 
.
Ответ: 
.
Упражнения:
1. 20 % изделий, выпускаемых данным предприятием, нуждаются в дополнительной регулировке. Наудачу отобрано 150 изделий. Найти среднее значение и дисперсию случайной величины X – числа изделий в выборке, нуждающихся в регулировке.
2. Вероятность попадания стрелком в мишень равна 
. Стрелком сделано 15 выстрелов. Случайная величина X – число попаданий в мишень. Найти математическое ожидание и дисперсию случайной величины X.
3. Найти среднее число лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, а вероятность выигрыша одного билета равна 0,1. Найти дисперсию числа успехов в данном опыте.
4. Проводятся три независимых испытания, в каждом из которых вероятность наступления некоторого события постоянна и равна p. Пусть X – число появлений события А в этом опыте. Найти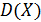 
, если известно, что 
.
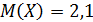5. Вероятность поражения цели при одном выстреле равна 0,4. Сколько надо произвести выстрелов, чтобы можно было ожидать в среднем 80 попаданий в цель?
|
|
|
Распределение Пуассона.
Дискретная случайная величина X имеет распределение Пуассона, если ее возможные значения: 1,2,3,.., m,…(счетное множество значений), а соответствующие вероятности выражаются формулой Пуассона
(1), где m =0,1,2,…; λ= np.
Распределение Пуассона является предельным для биномиального, когда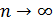 
(
), 
(
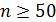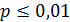) так, что λ= np = cons t (λ 
).
Примерами случайных величин, имеющих распределение Пуассона, являются: число вызовов на телефонной станции за время t, число опечаток в большом тексте; число бракованных деталей в большой партии; число -частиц, испускаемых радиоактивным источником и т.д. При этом считается, что события появляются независимо друг от друга с постоянной средней интенсивностью, характеризующий параметром λ= np.
Случайная величина X, распределенная по закону Пуассона, имеет следующий ряд распределения:
|
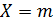
| 0 | 1 | 2 | … | m | … |
|
| 
| 
| 
| … | 
| … |
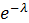
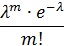
Контроль
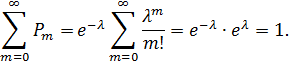
Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона: 
, 
.
Параметр λ пуассоновского распределения равен одновременно математическому ожиданию и дисперсии случайной величины X, имеющей это распределение. В этом состоит отличительная особенность изучаемого распределения, которая используется на практике (на основании опытных данных находят оценки для математического ожидания и дисперсии; если они близки между собой, т.е. основание считать, что случайная величина распределена по закону Пуассона).
Пример1. Вероятность попадания в цель при одном и выстреле равна 0,01. Какова вероятность того, что попаданий при 200 выстрелах составит не менее 5 и не более 10?
Решение: 1) 
; 2)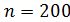 
; 3) λ= np = 200 
=2 .
Поэтому искомую вероятность будем находить используя формулу Пуассона. Случайная величина X – число попаданий. Требуется найти
.
Имеем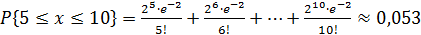 
.
Ответ: 0,053
Упражнения:
1. Проверяется партия из 10000 изделий. Вероятность того, что изделие окажется бракованным, равна 0,002. Найти математическое ожидание и дисперсию числа бракованных изделий в этой партии. Найти вероятность того, что в партии есть хотя бы одно бракованное изделие.
2. Дискретная случайная величина X распределена по закону Пуассона с параметром λ=0,324. Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины.
|
|
|
3. В магазин отправлены 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,002. Найти среднее число разбитых бутылок, вероятность того, что магазин получит более двух разбитых бутылок.
4. Сообщение содержит 1000символов. Вероятность искажения одного символа равна 0,004. Найти среднее число искаженных символов; найти вероятность того, что будет искажено не более трех символов.
5. Завод-изготовитель отправил на базу 12000 доброкачественных изделий. Число изделий поврежденных при транспортировке, составляет в среднем 0,05%. Найти вероятность того, что на базу поступит хотя бы 2 поврежденных; найти среднее число поврежденных изделий.
|
|
|
