 |
Математические операции над случайными величинами.
|
|
|
|
1. Произведением дискретной случайной величиной X на число 
называется дискретная величина 
, принимающая значения 
c теми же вероятностями, что и случайная величина X.
2. Квадратом дискретной случайной величины Х называется дискретная случайная величина 
, принимающая значения 
с теми вероятностями, что и случайная величина Х.
3. Суммой (разностью или произведением) д.с.в. X, принимающей значения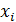 
с вероятностями 
, 
и д.с.в. Y, принимающая значения 
с вероятностями 
, 
называется дискретная случайная величина, принимающая все значения вида 
, , (
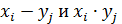) с вероятностями 
. Обозначается X + Y (X - Y и XY).
Выполняя указанные математические операции над случайными величинами, можно строить другие случайные величины и задавать их соответствующим рядом распределения.
Упражнения:
1. В урне 4 белых и 3 черных шара. Из нее наудачу извлекли три шара. Найти:
а) ряд распределения дискретной случайной величины У – числа извлеченных белых шаров;
б) вероятность события А={извлечено не менее 
шаров белого цвета}.
2. Монета бросается 4 раза. Построить многоугольник распределения случайной величины Х – числа выпадений герба.
3. Вероятность сдачи экзамена первым студентом равна 0,6, а вторым – 0,9. Составить ряд распределения случайной величины Х – числа студентов, успешно сдавших экзамен в случае, когда:
а) экзамены пересдавать нельзя
б) экзамен можно один раз пересдать.
4. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка равна 0,6, а для второго – 0,8.Найти и построить функцию распределения случайной величины Х – числа попаданий в мишень.
5. В урне 4 белых и 3 черных шара. Из нее последовательно вынимают шары до первого появления белого шара. Построить ряд и многоугольник распределения дискретной случайной величины Х – числа извлеченных шаров. Найти функцию распределения случайной величины Х и построить ее график.
|
|
|
6. В команде 16 спортсменов, из которых 6 перворазрядников. Наудачу выбирают двух спортсменов. Построить ряд распределения и функцию распределения числа перворазрядников среди выбранных.
7. Случайная величина Х задана рядом распределения. Составить:
а) многоугольник распределения;
б) функцию распределения и построить ее график.
| 0 | 1 | 2 | 3 |
| 0,1 | 0,3 | 0,4 | 0,2 |
8. Дискретная случайная величина Х задана рядом распределения. Найти: а) функцию распределения 
;
б) построить график функции ;
в) вероятности событий 
, 
, 
|
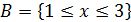| -2 | 1 | 2 | 3 |
|
| 0,08 | 0,4 | 0,32 | 0,2 |
9. Задана функция распределения случайной величины X. Найти ряд распределения, а также вероятности: 
.
10. Задана функция распределения с.в. X. Найти ряд распределения, а также вероятности: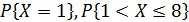 
.
. Непрерывные случайные величины.
В предыдущем параграфе было введено понятие случайной величины.
Если же множество возможных значений случайной величины несчетно, то такая величина называется непрерывной. (н.с.в.)
Несчетное множество означает, что значения нельзя пересчитать, ставя в соответствии им натуральные числа 1,2, …Значения непрерывной случайной величины могут лежать на отрезке, интервале, луче и т.д.
Например: случайная величина Z- время безотказной работы прибора.
Дадим теперь строгое определение случайной величины, исходя из теоретико-множественной трактовки основных понятий теории вероятностей.
Случайная величина X называют непрерывной, если ее функция распределения непрерывна в любой точке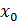 
и дифференцируема всюду, кроме быть может, отдельных точек.
В отличие от дискретных случайных величин вероятность отдельного значения для непрерывной случайной величины равна нулю:
|
|
|
.
Следовательно, для непрерывной случайной величины 
справедливы равенства
= 
= 
= 
.
Помимо функции распределения для непрерывных случайных величин, существует еще один удобный способ задания закона распределения – плотность вероятности.
Плотностью распределения вероятностей (плотностью распределения, плотностью вероятностей или просто плотностью) н.с.в. X называется производная ее функции распределения.
Обозначается через 
(
), если ясно о какой случайной величине идет речь.
И так, 
|
|
|
