 |
Перестановки с повторениями.
|
|
|
|
Пусть имеется совокупность из n элементов, среди которых m элементов первого, l-второго, k-третьего типа (n=m+l+k). Элементы повторяются α,β,γ раз соответственно. Такие комбинации называются перестановками с повторениями. Их число вычисляется по формуле
Пример 6: Из букв А,М,А,М разрезной азбуки составляется наудачу слово, состоящее из 4 букв. Какова вероятность, того что получится слово «МАМА»?
Решение: Событие A - получится слово «МАМА».
Найдем количество всевозможных исходов 
.
Чтобы найти количество благоприятных исходов, прокодируем карточки с буквами: 1-А, 2-М, 3- А, 4-М.
Слово «МАМА» получается в случаях комбинаций 2143, 4123, 2341, 4321, т.е. 
.
Тогда 
.
Ответ: 
.
Упражнения:
1. В урне 3 белых, 4 черных и 5 красных шаров. Найти вероятность того, что из урны вынули: а) красный шар; б) зеленый шар; в) два белых шара.
2. Код домофона состоит из 4 цифр, которые могут повторяться. Какова вероятность того, что случайно набирая цифры, можно угадать нужный код?
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
4. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
5. В параллели 51 учащийся, среди них два друга – Сергей и Вадим. Учащихся случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Сергей и Вадим окажутся в одной группе.
6. В группе туристов 10 человек. С помощью жребия они выбирают пятерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдет в магазин?
|
|
|
7. В группе туристов 50 человек. Их вертолетом в несколько приемов доставляют в труднодоступный район по 5 человек за рейс. Порядок, в котором вертолет перевозит туристов, случаен. Найдите вероятность того, что турист Д., полетит первым рейсом самолета.
8. Дано шесть карточек с буквами Н, М, И, Я, Л,О. Найдите вероятность того, что: 1) получится слово ЛОМ, если наугад одна за другой выбираются три карточки;2) получится слово Молния, если наугад одна за другой выбирается шесть карточек и располагаются, в ряд в порядке появления.
9. В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки:1) одинаковы, 2)различны?
10. В лифт 9-этажного дома вошли 4 человека. Каждый из них независимо друг от друга может выйти на любом этаже (начиная со второго). Какова вероятность того, что все вышли: а) на разных этажах; б) на одном этаже; в) на 5 этаже?
11. Из букв А,С,Н,Н,А,А разрезанной азбуки составляется наудачу слово, состоящее из букв. Какова вероятность того, что получится слово «АНАНАС»?
12. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя не глядя, переложил какие-то 3 монеты в другой карман. Найти вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
13. В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что: а) все они одного цвета; б) все они разных цветов; в) среди них два синих и 1 зеленый карандаш.
14. Двое друзей, А и В, стоят в очереди из 8 человек. Найти вероятность того, что: а) А и В стоят рядом; б) между А и В стоят два человека.
15. На 5 карточках написано по одной цифре из набора 1,2,3,4,5. Наугад выбираются две карточки. Какова вероятность того, что число на второй карточке больше чем на первой?
Геометрическая вероятность.
Чтобы преодолеть недостаток классического определения вероятности, состоящей в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).
|
|
|
Геометрической вероятностью события А называется отношение площади области D к площади области Ω, т.е.
Геометрическое определение вероятности события применимо и в случае, когда области Ω и D обе линейные или объемные, т.е.
Все три формулы можно записать в виде
где через mesобозначена мера (длина, площадь, объем) области.
Геометрическая вероятность обладает всеми свойствами, присущими классическому определению.
Пример 1: На отрезок ОА длины L числовой оси Ох наудачу поставлена точка B(x). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую 
. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
Решение: Разобъем отрезок ОА длины L точками C и D на три равные части. Требование задачи будет выполнено, если точка В(х) попадет на отрезок CD длины . Искомая вероятность 
.
Ответ: 
.
Пример 2: На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.
Решение: Площадь кольца 
. Площадь большого круга 
. Искомая вероятность 
.
Ответ: 0,75.
Пример 3: (задача о встрече) Два человека договорились о встрече между 9 и 10 часами утра. Пришедший первым ждет второго в течение 15 минут, после чего уходит (если не встретились). Найти вероятность того, что встреча состоится, если каждый наудачу выбирает момент своего прихода.
Решение: Пусть х – время прихода первого, а у- второго. Возможные значения х и у: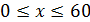 
, 
(в качестве единиц масштаба возьмем минуты), которые на плоскости Оху определяют квадрат со стороной, равной 60. Точки этого квадрата изображают время встречающихся.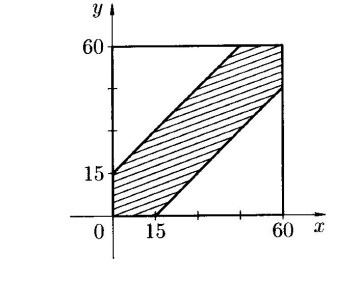 
рис. 2
Тогда Ω= 
; все исходы Ω равновозможны, т.к. лица приходят на удачу. Событие А – лица встретятся – произойдет, если разность между моментами их прихода будет не более 15 мин (по модулю), т.е. 
.
|
|
|
Неравенство 
, т.е. 
определяет область, заштрихованную на рисунке, т.е. точки полосы есть исходы, благоприятствующие встрече.
Искомая вероятность определяется по формуле
.
Ответ: 0,44.
Упражнения:
1. На отрезке 
случайно выбирается точка. Найти вероятность того, что расстояние от нее до правого конца отрезка не превосходит 1,6 единиц.
2. Стержень длины l разломан в двух наугад выбранных точках. Найти вероятность того, что из полученных отрезков можно составить треугольник.
3. На отрезке ОА длины L числовой оси ОХ наудачу нанесена точка В(х). Найти вероятность того, что отрезок ОВ и ВА имеют длину, большую 
.
4. Внутри эллипса 
расположен круг 
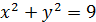. Найти вероятность попадания точки в кольцо, ограниченное эллипсом и кругом.
5. Точка взята наудачу внутри круга радиуса R. Найти вероятность того, что это точка окажется внутри вписанного в круг правильного треугольника. Предполагается, что вероятность попадания и не зависит от расположения внутри круга.
6. На квадрат 
брошена точка. Найти вероятность того, что точка будет удалена от центра квадрата не больше чем на 0,5.
7. Какова вероятность того, что корни уравнения 
будут действительными, если коэффициенты 
и 
уравнения выбираются наудачу из отрезка 
?
8. Два студента А и В условились встретиться в определенном месте во время перерыва между 13ч. и 13.50 ч.. Пришедший первым ждет второго в течение 10 минут, после чего уходит. Найти вероятность того, что встреча состоится, если приход каждого из них в течение указанных 50 мин. может произойти наудачу и моменты прихода независимы.
9. Пассажир может ехать на любом из автобусов двух маршрутов. Временные интервалы между моментами появления автобусов этих маршрутов равны соответственно 5 мин. И 12 мин. Найти вероятность того, что пассажир будет ждать не более 3 мин.
10. К преподавателю для сдачи зачета с 9 до 10 часов должны прийти 2 студента: Николай и Егор. Николаю для сдачи зачет потребуется 20 минут, а Егору – 10 минут. Найти вероятность того, что ни одному из них не придется ждать.
|
|
|
Теоремы сложения и произведения вероятностей.
Условная вероятность.
Во многих вопросах естествознания и техники встречаются события, вероятность которых зависит от того, произошло или не произошло некоторое другое событие.
Два события называются зависимыми, если вероятность появления одного из них зависит от появления или не появления другого.
Два события называются независимыми, если вероятность появления одного из них не зависит от появления или не появления другого.
Пример 1. Из урны, в которой находятся 8 белых и 12 черных шаров, последовательно вынимают два шара и обратно не возвращают. Событие А – первый вынутый шар черный, Событие В – второй вынутый шар черный. Выяснить, зависимы ли события А и В.
Решение: Пусть произошло событие А. Тогда в урне осталось 19 шаров, из них 11 черных. Поэтому вероятность события В равна 
(всего 19 вариантов, из них 11 благоприятствуют событию В).
Пусть теперь не произошло событие А, т.е. вынутый шар – белый. Поэтому вероятность события В равна 
. Видим, вероятность появления события В зависит от появления или не появления события А.
Ответ: зависимы.
Условной вероятностью вероятность события В при условии, что событие А произошло, называется отношению вероятности произведения этих событий к вероятности события А, причем Р(А) 
0, обозначается символом 
Для зависимых событий 
. Для независимых событий 
.
Вероятность Р(В), в отличии от условной, называется безусловной вероятностью.
В примере 1 
- второй вынутый шар черный при условии, что первый вынутый шар черный. 
. 
- второй вынутый шар черный при условии, что первый вынутый шар не черный. 
. Поэтому события А и В зависимы.
И так,
Пример 2: В примере 1. Найти вероятность того, что 2-ой шар окажется белым при условии, что 1-ый шар был белым.
Решение: 1спосо б: пусть А- 1-й шар черный, В – 2-й шар белый. Так как событие А произошло, то в урне осталось 19 шаров, из которых 8 белых. Поэтому 
2 способ: Найдем 
по формуле (1). Очевидно, что Р(А)= 
. Находим Р(АВ): n = 20 
19=380 – общее число исходов (появление двух шаров). Событию АВ благоприятствуют 
=96 исходов. Поэтому Р(АВ)= 
. Следовательно, 
. Ответ: 
.
Разностью (дополнением) А-В (А/В) событий А и В называется событие, происходящие тогда и только тогда, когда происходит событие А, но не происходит событие В. 
А/В= А-В=А 
.
Если В ⊂А, то вероятность разности А-В равна разности вероятностей: 
. 
Пример 3: Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что новая кофемолка прослужит больше двух лет, равна 0,81. Найти вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
|
|
|
Решение: 0,93
вероятность
1 год х 2 год 0,81
x +0,81=0,93
x =0,93-0,81=0,12.
Ответ: 0,12
В тех случаях, когда случайное событие состоит в том, что одновременно выполняется несколько элементарных событий, его вероятность определяется как вероятность произведения элементарных событий.
Вероятность произведения событий зависит от того, являются ли эти события зависимыми или независимыми.
Теорема 1. Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие А уже наступило: 
.
Следствие 1: Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
.
Пример 4: В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая обратно. Найдите вероятность того, что при первом испытании появится белый шар(событие А), при втором – черный (событие В) и при третьем – синий(событие С).
Решение: Вероятность появления белого шара в первом испытании 
. Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т.е. условная вероятность 
. Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором - черный, т.е. условная вероятность 
.
Искомая вероятность Р(АВС)= 
= 
= 
.
Ответ: 
Теорема 2. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей: 
.
Пример 5: Определим вероятность выпадения двух единиц при двух бросаниях кубика. А – при первом бросании выпало число 1, В – при втором бросании выпало число 1. Тогда АВ – оба раза выпало число 1.События А и В независимы, т.к. результаты при втором бросании кубика не зависят от того, что выпало при первом бросании. 
. Тогда 
.
Ответ: 
.
Следствие 2: Вероятность совместного появления нескольких независимых событий равна произведению вероятностей этих событий:
.
Пример 6: Имеется три ящика, содержащие по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение: Вероятность того, что из первого ящика вынута стандартная деталь равна Р(А) = 
. Вероятность того, что из второго ящика вынута стандартная деталь равна Р(В)= 
. В ероятность того, что из третьего ящика вынута стандартная деталь равна Р(С) = 
. Искомая вероятность Р(АВС)= Р(А) Р(В) Р(С) = 
=0,504.
Ответ: 0,504.
Теорема 1. Вероятность суммы несовместных событий А и В равна сумме их вероятностей: 
.
Следствие 1: Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
.
Пример 7: В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение: Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие А) Р(А)= 
. Вероятность появления синего шара (событие В) Р(В)= 
. События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность Р(А+В)=Р(А)+Р(В)= 
+ 
= .
Ответ: .
Теорема 2. Вероятность появления хотя бы одного из двух совместных событий А и В равна сумме их вероятностей без учета вероятности их совместного появления: 
.
Замечание 1: При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми.
Для независимых событий Р(А+В)=Р(А)+Р(В)-Р(А)Р(В); для зависимых Р(А+В)=Р(А)+Р(В)-Р(А)Р(В/А).
Замечание 2: если события А и В несовместны, то их совмещение есть невозможное событие и, следовательно, Р(АВ) =0. Формула (4) для несовместных событий принимает вид Р(А+В)=Р(А)+Р(В).
Пример 8: Определим вероятность выпадения хотя бы одной единицы при двух бросаниях кубика.
Решение: Событие А – при первом бросании выпало число 1, событие В – при втором бросании выпало число 1. Тогда А+В – появление хотя бы одной единицы в двух бросаниях кубика. Тогда 
.
Ответ: 
Формулы для определения вероятности суммы большего числа совместных событий достаточно громоздки. Так для трех совместных событий А, В, и С вероятность того, что наступило хотя бы одно из них, определяется по формуле:
Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС),
где АВ, АС, ВС – совместное наступлении событий попарно, а АВС – совместное наступление всех трех событий.
Теорема 3:Вероятность появления хотя бы одного из событий 
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 
, 
, …, 
: Р(А)=1-Р(
, …, 
)
Частный случай: если события имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий Р(А)=1- 
.
Пример 9: вероятности попадания в цель при стрельбе из трех орудий таковы: 
=0,8; 
=0,7, 
=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение: вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваем события 
(попадание первого орудия), 
(попадание второго орудия) и 
(попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям 
(т.е. вероятности промахов), соответственно равны:
=1-0,8=0,2; 
=1-0,7=0,3; 
=1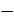 
0,9=0,1.
Искомая вероятность Р(А)=1 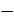0,2 0,3 0,1=0,994.
Ответ: 0,994.
Упражнения:
1. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар: а) белый; б) черный; в) синий; г) красный; д) белый или черный; е) синий или красный; ж) белый или черный или синий.
2. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,75, вторым стрелком – 0,8, третьим стрелком – 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.
3. Производится три выстрела по одной мишени. Вероятность попадания при каждом выстреле равна 0,5. Найти вероятность того, что в результате этих выстрелов будет только одно попадание.
4. В первом ящике 2 белых и 10 черных шаров. Во втором ящике 8 белых и 4 черных шаров. Из каждого ящика вынули по шару. Найти вероятность того, что оба шара белые.
5. В ящике 6 белых и 8 черных шаров. Из ящика вынули 2 шара(не возвращая вынутый шар в ящик). Найти вероятность того, что оба шара белые.
6. В урне 9 белых шаров и 1 черный шар. Вынули сразу 3 шара. Найти вероятность того, что все шары белые.
7. В условиях задачи 2 определить вероятность того, что в цель попадает хотя бы один стрелок.
8. В коробке лежат 20 компьютерных чипов, 4 из которых бракованные. Найти вероятность того, что дважды наудачу вытаскивая из коробки чип, мы обнаружим, что он бракованный:: а) с возвращением; б) без возвращения.
9. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек (выбор случайный). Найти вероятность того, что выбраны: а) два мальчика; б) две девочки; в) девочка и мальчик.
10. В фирме 500 работников, 300 из них имеют высшее образование, а 400 – среднее специальное образование, у 250 сотрудников - высшее образование и среднее специальное образование. Найти вероятность того, что случайно выбранный работник имеет или высшее образование, или среднее специальное образование, или то и другое.
11. Вероятность того, что сотрудник фирмы знает немецкий язык, равна 0,3, французский язык – 0,2 и знает оба языка – 0,02. Определить вероятность того, что наудачу выбранный сотрудник не знает ни немецкого, ни французского языка.
12. Найти вероятность того, что при бросании трех игральных костей хотя бы на одной из них выпадет 6 очков.
13. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если гроссмейстер А. играет черными, то А. выигрывает у гроссмейстера Б. с вероятностью 0,32. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
14. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,1. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
15. В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,03 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
16. В аэропорте два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35.. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
17. Помещение освещается фонарем с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,1. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
18. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,83. Вероятность того, что окажется меньше 11 пассажиров, равна 0,64. Найдите вероятность того, что число пассажиров будет от 11 до 17.
19. Вероятность того, что новый персональный компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,73. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
20. При подготовке к экзамену студент выучил 40 вопросов из пятидесяти вопросов программы. Экзаменационный билет содержит три разных вопроса. Вычислить вероятность того, что студент:
а) ответит на все три вопроса; б) ответит хотя бы на один из трех вопросов.
21. В первом ящике 2 белых и 10 черных шаров. Во втором ящике 8 белых и 4 черных шаров. Из каждого ящика вынули по шару. Определить вероятность того, что один из вынутых шаров белый, а другой черный.
22. Имеется 20 карточек, на которых записаны числа от1 до 20. Из них наугад выбирают одну карточку. Какова вероятность того, что на выбранной карточке будет число 20 или любое нечетное число?
23. Стрелок имеет 4 патрона и стреляет до первого попадания. Найти вероятность того, что число сделанных выстрелов будет нечетным, если вероятность попадания при одном выстреле р=0,75.
24. В урне 8 белых и 12 черных шаров, 2 игрока поочередно извлекают по одному шару, возвращая каждый раз обратно. Если этот шар черного цвета, выигрывает тот, кто первым извлекает белый шар. Найти вероятность выигрыша для каждого игрока, если каждому разрешается делать не более двух извлечений.
25. Определить вероятность того, что при подбрасывании трех игральных костей сумма выпавших очков будет более 14-ти и кратна 3-м.
26. Среди партии из 100 изделий имеется 10 бракованных. С целью контроля из этой партии отбирается наугад 7 изделий. Если среди них окажутся более двух бракованных, то бракуется вся партия изделий. Определить вероятность того, что партия изделий будет забракована.
27. Среди 100 лотерейных билетов есть 10 выигрышных. Какова вероятность того, что два наудачу выбранных билета окажутся выигрышными?
|
|
|
