 |
Вероятность случайного события.
|
|
|
|
Каждое равновозможное событие, которое может произойти в данном опыте, называется элементарным исходом.
Элементарные исходы, при которых наступает некоторое событие, называются элементарными исходами, благоприятствующими этому событию.
Пример 1: Бросают кубик один раз. Событию А – выпало четное число, благоприятствует выпадение 2, 4 или 6, т.е. элементарные исходы 
, 
Классическое определение вероятности: Вероятностью события А называется отношение числа исходов т, благоприятствующих событию А, к числу п всех равновозможных исходов опыта: 
.
Пример 2. В примере 1 найти вероятность того, что выпадет четное число.
Решение: Событию А – выпало четное число, благоприятствуют т=3 элементарных исходов, а всего возможно п=6 элементарных исходов. Следовательно 
.
Ответ: 
.
Пример 3. В урне находятся 10 шаров белого цвета и 5 красного цвета. Из урны извлекают один шар. Найти вероятность того, что шар будет белым.
Решение: Событие А – изъят из урны шар белого цвета, благоприятствуют т=10 элементарных исходов, а всего возможно п=15 элементарных исходов. Следовательно 
.
Ответ: 
Простейшие свойства вероятности.
1. 
;
2. Вероятность достоверного события равна 1,т.е.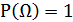 
;
3. Вероятность невозможного события равна 0, т.е. 
;
4. 
, где А – случайное событие.
Определяя вероятность события А в примере 3, мы заранее знали о том, сколько белых и сколько красных шаров находится в урне. Как же следует поступить с расчетом вероятности событий А, если предварительных сведений нет?
Очевидно, что следует произвести эксперимент: вынимать шар из урны, фиксировать (записывать), какого цвета шар был изъят, и класть его обратно. Повторяя эти действия достаточно большое количество раз – n (100, 1000 и более раз), можем подсчитать, сколько раз произошло событие А, т.е. был вынут белый шар. Обозначим через 
– частоту события А, число «удачных» изъятий, в том смысле, что интересующее нас событие А осуществилось, и n - результатов оказались «неудачными» - событие А не произошло.
|
|
|
Отношение числа «удачных» исходов к числу всех испытаний, т.е. 
, называется относительной частотой (или частостью) события А.
Частность обладает свойством статистической устойчивости: с увеличением числа опытов (т.е. n) она принимает значения, близкие к некоторому постоянному числу.
Статистическое определение вероятности: Вероятностью события А называется постоянное число, около которого колеблется относительная частота события А при достаточно большом числе испытаний (опытов), т.е. 
.
При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности.
Можно показать, что при статистическом определении вероятности события сохраняются свойства вероятности события, справедливые в условиях классической схемы.
Упражнения:
1. В сборнике билетов по химии всего 50 билетов, в 20 из них встречается вопрос по углеводородам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам.
2. В сборнике билетов по физике всего 25 билетов, в 13 из них встречается вопрос по оптике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по оптике.
3. На тарелке лежат пирожки: 5 с капустой и 4 с картошкой. Таня берет один пирожок. Найти вероятность того, что выбранный пирожок окажется с картошкой.
4. В среднем из 50 аккумуляторов, поступивших в продажу, 7 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
5. В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
|
|
|
6. Сережа с папой решили покататься на колесе обозрения. Всего на колесе тридцать восемь кабинок, из них 5 синих, 23 зеленых, остальные оранжевые. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность, что Сережа прокатится в оранжевой кабинке.
7. В чемпионате по гимнастике участвуют 20спортсменок: 8изРоссии, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.
8. На семинар приехали 4 ученых из Норвегии, 2 из Испании и 6 из Италии. Порядок докладов определяется жеребьевкой. Найдите вероятность того, что одиннадцатым окажется доклад ученого из Италии.
9. Фабрика выпускает сумки. В среднем на 140 качественных сумок приходится пятнадцать сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до десятых.
10. На борту самолета 19 кресел расположены рядом с запасными выходами и 13 – за перегородками, разделяющими салоны. Все эти места удобны для пассажира высокого роста. Остальные места неудобны. Пассажир Л. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Л. достанется удобное место. Если всего в самолете 400 мест.
11. В чемпионате мира участвуют 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1,1,1,1, 2,2,2,2,3,3,3,3,4,4,4,4,5,5,5,5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
12. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 6, но не дойдя до отметки 9.
13. В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдет приз в своей банке.
|
|
|
14. Какова вероятность того, что случайно выбранное натуральное число от 35 до 46 делится на 5?
15. Ученика попросили назвать число от1до100. Какова вероятность того, что он назовет число кратное пяти?
16. Конкурс исполнителей длится 4 дня. Всего заявлено 40 выступлений - по одному из каждой страны. В первый день запланировано 25 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что выступление представителя России состоится в третий день конкурса.
17. Катя дважды бросает игральный кубик. В сумме у нее выпало 6 очков. Найти вероятность того, что при одном из бросков выпало 5 очков.
18. В случайном эксперименте симметричную монету бросают дважды. Найти вероятность того, что один раз выпадет орел, а другой - решка.
19. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет оба раза.
20. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз.
21. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Витязь» по очереди играет с командами «Атлант» и «Титан». Найдите вероятность того, что команда «Витязь» не выиграет право первой владеть мячом ни в одном матче.
22. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Байкал» по очереди играет с командами «Атлант», «Енисей», «Вилюй» и «Иртыш». Найдите вероятность того, что ровно в двух матчах право владеть мячом выиграет «Байкал».
23. В случайном эксперименте бросают две игральные кости. Найти вероятность того, что в сумме выпадет 3 очка. Результат округлите до сотых.
24. Аня и Яна играют в кости. Они бросают кость по одному разу. Выигрывает тот, кто выбросил больше очков. Ничья, если очков поровну. Аня выкинула 3 очка. Затем кубик бросает Яна. Найдите вероятность того, что Яна выиграет.
25. Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 11 участников из России, в том числе Петр Трофимов. Найдите вероятность того, что в первом туре Петр Трофимов будет играть с каким-либо шахматистом из России.
|
|
|
26. За круглый стол на 11 стульев в случайном порядке рассаживаются 9 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
27. В некоторой типографии 10% отпечатанных справочников имеют дефект. При контроле качества продукции выявляется 60% дефектных справочников. Остальные справочники поступают в продажу. Найдите вероятность того, что случайно выбранный при покупке справочник имеет дефект. Ответ округлите до тысячных.
28. На фабрике керамической посуды 15% произведенных кружек имеют дефект. При контроле качества продукции выявляется 80% дефектных кружек. Остальные кружки поступают в продажу. Найдите вероятность того, что случайно выбранный при покупке кружка не имеет дефектов. Ответ округлите до тысячных.
29. В некотором городе из 8000 появившихся на свет младенцев 4140 мальчики. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
30. В некотором городе из 2000 появившихся на свет младенцев 990 девочек. Найдите частоту рождения мальчиков в этом городе. Результат округлите до тысячных.
Элементы комбинаторики.
Чтобы пользоваться данным определением вероятности, нужно уметь подсчитывать общее число исходов эксперимента и число благоприятных исходов. Такой подсчет сводится к перебору вариантов.
Раздел математики, в котором исследуются различные задачи на перебор, называется комбинаторикой.
Типы комбинаций:
1. Размещения;
2. Сочетания;
3. Перестановки
Существуют две схемы выбора m элементов (0<m≤n) из исходного множества: без возвращения(без повторений) и с возвращением (с повторением).
Схемы без возвращения.
Размещение.
Если составляются такие комбинации из n элементов по m, которые отличаются не только составом элементов, но и порядком их следования, то они называются размещениями. Их число находится по формуле
Пример 1. В урне находятся карточки с цифрами от 0 до 5. Наугад достают две карточки и складывают подряд. Найти вероятность того, что событие А – полученное двузначное число кратно семи.
Решение: Всего исходов п = 
.
Благоприятные исходы – это числа 14, 21, 35, 42, т.е. т =4.
Получаем 
.
Ответ: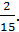 
Сочетание.
Если составляются такие комбинации из n элементов по m, которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Их число находится по формуле
|
|
|
Пример 2: В урне 10 шаров, из них 3 белых. Найти вероятность того, что из четырех наугад выбранных шаров ровно 1) событие А - один будет белый; 2) событие В – белых шаров будет два.
Решение: Всего исходов п = 
. В первом случае при благоприятном исходе среди четырех шаров один белый, а остальные три – черные. Один белый шар можно выбрать тремя способами (их всего три), три черных шара можно выбрать 
способами, т.к. черных шаров в урне 7.
Каждый из трех белых шаров может сочетаться с любой из черных троек. Таким образом, благоприятных исходов т = 
.
Получаем 
.
Во втором случае при благоприятном исходе среди четырех шаров два белых и два черных. Пару белых шаров можно выбрать 
способами.
Для пары черных шаров число способов выбора 
.
Каждая пара белых может сочетаться с каждой парой черных, поэтому
т =3·21=63. Получаем 
Ответ: 0,5 и 0,3
Перестановки.
Если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановками. Их число равно
Пример 3: На книжной полке выставлены 4 тома романа Толстого Л.Н. «Война и мир». Найти вероятность того, что на первом месте будет стоять первый том.
Решение: Событие A – на первом месте будет стоять первый том.
Найдем общее количество исходов 
. Количество благоприятных исходов 
1 
=6.
Тогда 
Ответ: 
.
Схемы с возвращением.
Размещения с повторением.
Размещения с повторением могут отличаться друг от друга элементами, их порядком и количеством повторений элементов. Число всех размещений из n элементов по m с повторениями обозначается символом 
. Их число находится по формуле
Пример 4. Телефонная книга раскрывается наудачу и выбирается случайный номер телефона. Считая, что телефонные номера состоят из семи цифр, причем все комбинации равновероятны, найти вероятность того, что все цифры в номере различны. (Условие задачи разрешает любые номера 0012413, 0000000).
Решение: Событие A - все цифры в номере различны.
Поскольку всего цифр 10, а номера семизначные, то общее число номеров равно 
. Благоприятные исходы составляют все различные наборы из семи цифр, отличающихся также порядком.
Значит т = 
.
Тогда 
Ответ: 0,6.
Сочетания с повторением.
Сочетания с повторениями из n элементов по m элементов состоят из различных элементов, из m каких угодно и как угодно повторяющихся элементов из числа n или не содержать их вообще. Число всех сочетаний с повторениями обозначается 
. Их число находится по формуле
Пример 5. В кондитерской продается семь видов пирожных. Очередной покупатель выбил чек на четыре пирожных. Найти вероятность того, что заказаны:
1) А - пирожные одного вида;
2) В - пирожные разных видов;
3) С - по два пирожных разных видов.
Решение: Выбор пирожных укладывается в схему выбора с возвращением без упорядочения.
Поэтому общее число исходов равно п = 
.
В первом случае благоприятных исходов т =7. 
.
Во втором случае благоприятными являются всевозможные наборы из четырех различных пирожных, выбранных из 7 (порядок не важен).
Число благоприятных исходов т = 
.
.
В третьем случае благоприятный исход представляет собой две пары одинаковых пирожных.
Таких наборов ровно столько, сколько различных пар можно составить из семи пирожных,
т.е. т =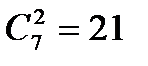 
. 
.
Ответ: 1) 
, 2) 
, 3) 0,1.
|
|
|
