 |
Среднее квадратическое отклонение
|
|
|
|
Т.к. дисперсия характеризует квадрат отклонений значений случайной величины от математического ожидания, то для оценки рассеивания возможных значений случайной величины вокруг ее среднего значения, часто используют среднее квадратическое отклонение.
Среднее квадратическое отклонение случайной величины Х называют квадратный корень из дисперсиии:

Обозначается так:  ,
,  ,
,  .
.
Из свойств дисперсии вытекают следующие свойства среднего квадратического отклонения:  ,
,  ,
, 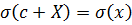 ,
,  .
.
Пример 2: Дискретная случайная величина Х задана рядом распределения
| Х | -1 | 0 | 1 | 2 |
| Р | 0,2 | 0,1 | 0,3 | 0,4 |
Найти M (X), D (X),  .
.
Решение: M (X) = (-1)  0,2+0
0,2+0  0,1+1
0,1+1  0,3+2
0,3+2  0,4=0,9.
0,4=0,9.
D (X) =  .
.
или
 .
.
 .
.
Ответ: 1) 0,9; 2)  ; 3)
; 3)  .
.
Модой дискретная случайная величина X называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями, обозначается через 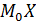 – точка максимума (локального) плотности
– точка максимума (локального) плотности  .
.
Медианой  непрерывная случайная величина X называется такое ее значение
непрерывная случайная величина X называется такое ее значение  , для которого
, для которого

т.е. одинаково вероятно, окажется ли случайная величина X меньше  или больше
или больше  .
.
Для дискретной случайной величины медиана обычно не определяется.
Математическое ожидание и дисперсия являются частными случаями следующих более общих понятий – моментов случайной величины.
Начальным моментом порядка k случайной величины X называется математическое ожидание k–й степени этой величины, обозначается через 
Таким образом, по определению
 = M (
= M ( )
)
Для дискретной случайной величины начальный момент выражается суммой:

а для непрерывной случайной величины – интегралом:

В частности,  , т.е. начальный момент 1-го порядка есть математическое ожидание.
, т.е. начальный момент 1-го порядка есть математическое ожидание.
Центральным моментом порядка k случайной величины X называется математическим ожиданием величины  , обозначается через
, обозначается через  .
.
|
|
|
Таким образом, по определению
 .
.
В частности,  , т.е. центральный момент 2-го порядка есть дисперсия;
, т.е. центральный момент 2-го порядка есть дисперсия;  .
.
Для дискретной случайной величины:

а для непрерывной случайной величины:

Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядков, называемые соответственно коэффициентами асимметрии и эксцесса.
Коэффициентом асимметрии («скошенности») A случайной величины X называется величина

Если A > 0, то кривая распределения более полога справа от 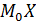 .
.
Если A < 0, то кривая распределения более полога слева от 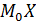 .
.
Коэффициентом эксцесса («островершинности») E случайной величины X называется величина

Величина E характеризует островершинность или плосковершинность распределения. Если E > 0 – более островершинные, а распределения «плоcковершинные» имеют E<0.
Кроме рассмотренных выше числовых характеристик случайной величины, в приложениях используются так называемые квантили.
Квантилью уровня p случайной величины X называется решение уравнения
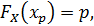
где p – некоторое число, 0 < p < 1.
Квантили  и
и  имеют свои названия: нижняя квартиль, медиана
имеют свои названия: нижняя квартиль, медиана  , верхняя квартиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0,25.
, верхняя квартиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0,25.
Упражнения:
1. Задан закон распределения дискретной случайной величины Х. Найти математическое ожидание и дисперсию случайных величин  ,
, 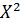 .
.
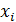
| -2 | -1 | 0 | 1 | 2 | 3 |
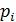
| 0,1 | 0,2 | 0,25 | 0,15 | 0,1 | 0,2 |
2. Закон распределения случайной величины X задан таблицей распределения. Найти коэффициент с, 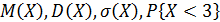 .
.
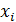
| 1 | 2 | 3 | 4 |
| 
| 
| 
| c |
3. Математическое ожидание и дисперсия дискретной случайной величины Х соответственно равны  и
и  . Найти математическое ожидание и дисперсию случайной величины 4 X -1.
. Найти математическое ожидание и дисперсию случайной величины 4 X -1.
4. Случайные величины X и Y независимы, причем их дисперсии  и
и  . Найти
. Найти  , если
, если  .
.
|
|
|
5. Брошены 10 игральных костей. Найти 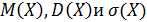 , где случайная величина Х – сумма очков, выпавших на всех игральных костях.
, где случайная величина Х – сумма очков, выпавших на всех игральных костях.
6. Независимо испытываются на надежность 3 прибора. Вероятности выхода из строя каждого прибора одинаковы и равны 0,6. Найти M (X) и  , где случайная величина X – число вышедших из строя приборов.
, где случайная величина X – число вышедших из строя приборов.
7. Плотность вероятности случайной величины Х задается формулой  =
= 
Найти ее числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, асимметрию и эксцесс.
8. Плотность вероятности непрерывной случайной величины Х задается формулой  =
= 
Найти ее числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение.
9. Плотность распределения случайной величины X задается формулой 
Найти  .
.
10. Найти моду, медиану, математическое ожидание и квантиль уровня 0,75 случайной величины  с плотностью вероятности
с плотностью вероятности  =
= 
11. Плотность вероятности случайной величины Х задается формулой  =
= 
Найти моду, медиану, математическое ожидание и квантиль порядка 0,25.
12. Непрерывная случайная величина Х задана функцией распределения 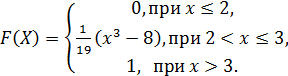
Найти моду, медиану, математическое ожидание случайной величины.
|
|
|


