Формула полной вероятности.

Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса.

Формула полной вероятности часто используется на практике в задачах экономического анализа и в научно-исследовательских работах. В тех случаях, когда необходимо определить вероятность какого-то случайного события, наступление которого зависит от внешнего воздействия, невозможно однозначно оценить вероятность, необходимо принимать во внимание влияние внешних факторов.

Теорема 1: Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

События  обычно называют гипотезами (заранее неизвестно какое наступит); они исчерпывают все возможные предположения(гипотезы) относительно исходов как бы первого этапа опыта, событие А – один из возможных исходов второго опыта.

По формуле полной вероятности можно вычислять, например, вероятность попадания на сборку стандартной детали из общей партии деталей, изготовленных на нескольких станках, если для каждого станка известны его доля в общем выпуске деталей и процент стандартных деталей в общем числе выпускаемых деталей, а также другие аналогичные задачи.

Пример 1: в сборочный цех завода поступает 40% деталей из I цеха и 60% - из II цеха. В I цехе производится 90% стандартных деталей, а во II- 95%. Найти вероятность того, что наудачу взятая сборщиком деталь окажется стандартной.

Решение: взятие детали можно разбить на два этапа.

Первый – это выбор цеха. Имеется две гипотезы:  – деталь изготовлена I цехом, - II цехом. Второй этап – взятие детали. Событие А - взятая наудачу деталь стандартна. Очевидно, события  и  образуют полную группу, Р()=0,4, Р()=0,6. Числа 0,90 и 0,95 являются условными вероятностями события А при условии гипотез  и  соответственно, т.е. Р()=0,90 и Р( =0,95. По формуле (1) находим

Р(А)= Р()Р() + Р() = 0,4 0,90+0,6  0,95=0,93.

Ответ: 0,93.

Упражнения:

1. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

2.  Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.

3.  Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больного гепатитом пациентов анализ дает положительный результат с вероятностью 0,8. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,03. Известно, что 43% пациентов, поступающих с подозрением на гепатит, действительно больным гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

4. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнется.            

5. Чтобы поступить в институт на специальность «Прикладная математика», абитуриент должен набрать на ЕГЭ не менее 65 баллов по каждому из трех предметов: математика, русский язык и информатика. Чтобы поступить на специальность «Механика», нужно набрать не менее 65 баллов по каждому из трех предметов: математика, русский язык и физика. Вероятность того, что абитуриент А. получит не менее 65 баллов по математике, равна 0,6, по русскому языку – 0,7, по информатике 0,6 и по физике – 0,5. Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.        

6. В Сказочной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,6 погода завтра будет такой же, как и сегодня. Сегодня 25 октября, погода в Сказочной стране хорошая. Найдите вероятность того, что 28 октября в Сказочной стране будет отличная погода.

7. Имеется 4 урны. В первой урне 1 белый и 1 черный шары. Во второй урне 2 белых и 3 черных шара. В третьей урне 3 белых и 5 черных шаров. В четвертой урне 4 белых и 7 черных шаров. Событие  – выбор i -ой урны (i = 1,2,3,4). Дано, что вероятность выбора i-ой урны равна 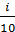. Выбирается наугад одна из урн и вынимается из нее шар. Найти вероятность того, что этот шар белый.

8. Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,04, а в период экономического кризиса - 0,13. Предположим что вероятность того, что начнется период экономического роста, равна 0,65. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?

9. В учебном пособии по физике имеется 45 задач к первому разделу, 30 задач ко второму и 35 задач к третьему разделу дисциплины. Шансы студента правильно решить задачу из первого раздела оцениваются в 80%, из второго – в 65%, из третьего – 85%. Студент наудачу открывает пособие, определите вероятность, что он решит случайно выбранную задачу.

10. Изображена схема дорог. Туристы выходят из пункта А, выбирая наугад на развилке дорог один из возможных путей. Какова вероятность того, что они попадут в пункт В?

11. 45% телевизоров, имеющихся в магазине, изготовлены на 1-м заводе, 15% - на 2-м заводе, остальные – на 3-м заводе. Вероятность того, что телевизоры, изготовленные на этих заводах, не потребуют ремонта в течение гарантийного срока, равна 0,96; 0,84; 0,90 соответственно. Найти вероятность того, что купленный наудачу телевизор выдержит гарантийный срок работы.

12. Д ля улучшения качества радиосвязи используются два радиоприемника. Вероятность приема сигнала каждым приемником равна 0,8, и эти события (прием сигнала приемником) независимы. Определить вероятность приема сигнала, если вероятность безотказной работы за время сеанса радиосвязи для каждого приемника равна 0,9.

 

 Формула Байеса

Современные методы управления различными процессами в экономике, экологии, медицине и других областях науки и производства непременно используют анализ окружающей действительности посредством математических методов, к которым относятся и вероятностные методы. Имея предварительные(априорные) значения вероятностей интересующих исследователя событий, он проводит опыт или отбор данных из источников информации, таких как выборки, отчеты и т.д., получая при этом дополнительную информацию об интересующем его событии.

Имею эту новую информацию, можно уточнить, пересчитать значения априорных вероятностей. Новые значения вероятностей для тех же интересующих нас событий будут уже апостериорными (послеопытными) вероятностями. Теорема Байеса (теорема гипотез) дает нам правило для вычисления таких вероятностей.

Формула Байеса позволяет переоценить вероятности гипотез , принятых до опыта и называемых априорными(доопытные) по результатам уже проведенного опыта, т.е. найти условные вероятности Р(), которые называют апостериорными (послеопытные).

Теорема 1: Пусть события  образуют полную группу событий. Тогда условная вероятность события  (i = ) при условии, что событие А произошло, задается формулой

 (формула Байеса), где Р( )Р( ) +…+ Р( ) Р( )- формула полной вероятности.

Пример 1: в примере 1  найти вероятность того, что эта стандартная деталь изготовлена II цехом.

Решение: определим вероятность гипотезы  при условии, что событие А (взятая деталь стандартна) уже произошло, т.е. :

= = .

Ответ: .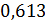

В настоящее время формулы Байеса находят широкое применение при решении проблем управления, связанных с принятием административных решений, когда приходится сталкиваться с недостаточной информацией о закономерностях в экономике и промышленности. По мере накопления дополнительной информации производится корректировка решений. Например, одной из таких проблем является принятие окончательного решения при входном контроле партии деталей. При этом возможны следующие варианты решений:

1) Принять всю партию, запустив ее в производство;

2) Проконтролировать каждое изделие в партии, заменяя или исправляя при этом дефектные изделия;

3) Заблокировать всю партию.

Использование формул Байеса позволяет принять наилучшее решение.

 

Упражнения:

1. Имеется три одинаковых по виду ящика. В первом ящике 20 белых шаров. Во втором ящике 10 белых и 10 черных шаров. В третьем ящике 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.

2. Среди студентов института 30% первокурсники, 35% студентов учатся на втором курсе, на третьем и четвертом курсе их 20% и 15% соответственно. По данным деканата известно, что на первом курсе 20% студентов сдали сессию только на отличные оценки, на 2-м – 30%, на 3-м – 35%, на 4-м – 40% отличников. Наудачу вызванный студент оказался отличником. Чему равна вероятность того, что он (или она) - третьекурсник.

3. Техническое устройство выйдет из строя, если откажут не менее двух из трех независимо работающих элементов. Вероятность отказов 1-ого, 2-ого, 3-его элементов соответственно равны 0,2; 0,4; 0,3. Известно, что устройство отказало. Найти вероятность того, что отказали 1-ый и 2-ой элементы.

4. Прибор содержит две микросхемы. Вероятность выхода из строя в течение 10 лет первой микросхемы равна 0,07, а второй – 0,10. Известно, что из строя вышла одна микросхемы. Какова вероятность того, что вышла из строя первая схема.

5. При оформлении групп студентов имеется два списка с фамилиями первокурсников. В 1-ом списке фамилии 16 девушек и 13 юношей, во 2-ом – 14 девушек и 17 юношей. Из 1-ого списка случайно перенесли одну фамилию во второй список. Определите вероятность того, что из первого списка была перенесена фамилия девушки, если при случайном выборе из второго списка была изъята фамилия юноши.

6. В магазин поступают одинаковые изделия трех заводов, причем 1-й завод поставил 50 изделий, 2-й – 30, 3-й – 20 изделий. Среди изделий 1-го завода 70% первосортных, а среди изделий 2-го – 80%, 3-го – 90% первосортных. Куплено одно изделие. Оно оказалось первосортным. Какова вероятность того, что это изделие выпущено 1-м заводом?

 

. Схема испытаний Бернулли.

Пусть в результате некоторого случайного испытания может произойти или не произойти определенное событие А. Если событие произошло, будем называть испытание успешным, а само событие – успехом. Испытание повторяется п раз. При этом соблюдаются следующие условия:

- вероятность успеха Р(А)=р в каждом испытании одна и та же;

- результат любого испытания не зависит от исходов предыдущих испытаний.

Такая последовательность испытаний с двумя исходами (успех/неудача) называется последовательностью независимых испытаний Бернулли или схемой Бернулли.

Теорема 1: Если производится n независимых испытаниях, в каждом из которых вероятность появления события А равна р, а вероятность его не появления равна q=1-p, то вероятность того, что событие А произойдет m раз определяется формулой Бернулли   (1), где m =0,1,2,…, n.

Пример 1. В урне 3 белых и 2 черных шара. Из урны 4 раза наугад вынимают по 2 шара и возвращают обратно. Найти вероятность того, что ровно 3 раза вынули шары разного цвета.

Решение: А- успех: вынули шары разного цвета. Найдем вероятность р успеха в единичном испытании. Имеем исходов.

Благоприятными являются исходы с шарами разного цвета: при этом каждый из 3 белых шаров может сочетаться с любым из 2 черных. Значит . . Тогда .

По формуле Бернулли получаем .

Ответ: 0,3456.

Можно показать, что в n испытаниях Бернулли существует целое число , которому соответствует максимальное значение вероятности. Это число называется наивероятнейшим числом успехов.

Наивероятнейшее число успехов  удовлетворяет двойному неравенству  или (2).

Может оказаться так, что в полученном интервале содержится несколько целых чисел. Тогда все они являются наивероятнейшими и имеют одинаковую вероятность – наибольшую среди всех значений .

Пример 2: Всхожесть семян данного растения имеет вероятность 0,8. Найти наиболее вероятное число проросших семян из 5 посеянных.

Решение: По условию задачи . Следовательно, . Подставляя эти данные в формулу (2), получим

2;

.

Ответ: 4

Если в каждом из независимых испытаний вероятности наступление события А разные, то вероятность того, что события А наступит m раз в n опытах, равна коэффициенту при m -й степени многочлена

(3), где  – производящая функция.

Пример 3: Производится три независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны р=0,9. Какова вероятность: а) промаха; б) одного попадания; в) двух попаданий; г) трех попаданий?

Решить задачу в случае, если вероятности попадания при разных выстрелах различны:  .

Решение: в данном случае n=3, р=0,9, q=0,1. Пользуясь формулой Бернулли, находим:

а) =0,001 – вероятность трех промахов;

б) =3 0,9 0,01=0,027 – вероятность одного попадания;

в) =3 0,81 0,1=0,243 – вероятность двух попаданий;

г) = =0,729 - вероятность трех попаданий.

Если вероятности при разных выстрелах различны, то производящая функция имеет вид .

Откуда находим вероятность трех, двух, одного попадания, промаха соответственно: , , , =0,006. (Контроль .)

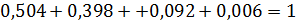Ответ: ; ; ; 0,006.

Упражнения:

1. Биатлонист попадает в мишень с вероятностью 0,9. Он стреляет пять раз. Найдите вероятность того, что он попадет в мишень все пять раз.

2. Биатлонист попадает в мишень с вероятностью 0,7. Он стреляет пять раз. Найдите вероятность того, что он не попадет в мишень все пять раз.

3. Биатлонист попадает в мишень с вероятностью 0,9. Он стреляет пять раз. Найдите вероятность того, что он попадет в мишень ровно один раз.

4. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно 1 будет без брака.

5. Что вероятнее выиграть у равносильного противника шахматиста: две партии из четырех или три из шести? Ничьи во внимание не принимаются.

6. Монету подбрасывают 10 раз. Какова вероятность того, что герб выпадет: а) 4 раза; б) ни разу; в) хотя бы один раз.

7. В тире стрелок проводит 7 выстрелов по мишени с вероятностью попадания каждого 0,8. Какова вероятность того, что будет не менее 5 попаданий.

8. Прививка от гриппа дает положительный результат в 70% случаев. Найти вероятность, что в группе из 15 человек более чем для двух она будет бесполезной.

9. На склад из производственного цеха поступает в среднем 5% нестандартных деталей. Найти вероятность того, что среди взятых наудачу 10 деталей 2 будут нестандартными.

10. В семье трое детей. Какова вероятность того, что: а) все они мальчики; б) один мальчик и две девочки. Считать вероятность рождения мальчика 0,51, а девочки – 0,49.

11. Прибор состоит из трех независимо работающих элементов. Вероятность отказов элементов за время t различны и соответственно равны: , , 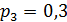. Найти вероятности того, что за время t откажут: а) все элементы; б) два элемента; в) один элемент; г) ноль элементов.

12. Из четырех орудий произведен залп по цели. Вероятность попадания в цель для 1-го орудия равна 0,8; для 2-ого – 0,7; для 3-его – 0,6; для 4-ого – 0,5. Найти вероятность того, что в цель попадут:

а) два орудия; б) три орудия; в) четыре орудия.

13. Три биатлониста независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого равна 0,9, для второго - 0,85, для третьего - 0,8. Найти вероятность того, что будут закрыты две мишени из трех.

14. Батарея дала 10 выстрелов по объекту, вероятность попадания в который при отдельном выстреле равна 0,4 и не зависит от результатов предыдущих выстрелов. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.

15. В урне 100 белых и 80 черных шаров. Из урны извлекают n шаров (с возвратом каждого вынутого шара). Наивероятнейшее число появлений белого шара равно 11. Найти n.

 

§9. Теорема Пуассона

Теорема 1: Если число испытаний неограниченно увеличивается (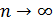) и вероятность p наступления события А в каждом испытании неограниченно уменьшается () p , но так, что их произведение n p является постоянной величиной (n p =λ= const), то вероятность  удовлетворяет предельному равенству

Выражение (1) называется асимптотической формулой Пуассона.

Из предельного равенства (1) при больших n и малых p вытекает приближенная формула Пуассона , λ = n p, m =0,1,2,… (2).

Приближенную формулу (2) обычно используют, когда , λ= n p .

Формула Пуассона находит применение в теореме массового обслуживания.

Пример 1. Завод «Крым» отправил в Москву 1500 стеклянных бутылок лимонада. Вероятность того, что в пути бутылка может разбиться, равна 0,002. Найти вероятность того, что в пути будет разбито не более 4- бутылок (событие А).

Решение: Искомая вероятность равна

.

Так как n =1500, p =0,002, то λ=[np]=3. Вероятность события А найдем, используя формулу Пуассона (2): + + + =0,8152.

Ответ: 0,8152.

Формулу Пуассона можно считать математической моделью простейшего потока событий.

Пример 2. Телефонная станция обслуживает 2000 абонентов. Вероятность позвонить любому абоненту в течение часа равна 0,003. Какова вероятность того, что в течение часа позвонят 5 абонентов?

Решение: Среднее число позвонивших в течение часа абонентов равно 2000 0,003=6 (λ= np). Стало быть, .

Ответ: .

 

Упражнения:

1. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,007. Поступило 1000 вызовов. Определить вероятность 9 «сбоев».

2. Вероятность выхода прибора из строя равна . Определить вероятность того, что из  приборов   выйдут из строя.

3. Завод-изготовитель отправил на базу 12000 доброкачественных изделий. Число изделий поврежденных при транспортировке, составляет в среднем 0,05%. Найти вероятность того, что на базу поступит: а) не более 3 поврежденных изделий; б) хотя бы 2 поврежденных.

4. В тысячу ящиков разложили изделия, среди которых было 200 бракованных. Оценить вероятность того, что в определенном ящике не менее трех бракованных изделий.

5. На лекции по теории вероятностей присутствуют 84 студента. Какова вероятность того, что среди них есть два студента, у которых сегодня день рождения?

6. Сколько в среднем должны содержать изюм булочки, чтобы вероятность того, что в булочке найдется хотя бы одна изюмина, было не меньше 0,99.

 

Предыдущая123456789Следующая

Поделиться:

Воспользуйтесь поиском по сайту: