Алексей Савватеев: Здравствуйте!

Лекция 1

 

Алексей Савватеев: Здравствуйте!

Аудитория: Здравствуйте!

А. С.: Для начала я расскажу кое‑ что о себе.

В 1990 году я закончил 57‑ ю школу г. Москвы. Может быть, кто‑ то из вас ее знает. Тогда это была математическая школа. Но в 1989 году по инициативе нашей учительницы литературы Зои Алексан­дровны Блюминой было принято решение набрать гуманитарный класс, чтобы уравновесить огромный перекос учащихся в мужскую сторону в нашей школе. Я был в 11‑ м классе, а набрали 9‑ й.

Зачем я об этом говорю? У меня в гуманитарном классе была подруга, которой я объяснял математику. Однажды надо было ре­шить уравнение типа sin ж = ^ Я объяснял, объяснял, объяснял,

_ai, o_I„_H, _ICpC_, _raiCKpOTIJ₁, „_Kp™, »o_ypMira„„_8i, ^I

Она говорит: «Стой... Там же был sina; ».

Я начинаю объяснять: «Это закрытый терм, замкнутая пере­менная, она уничтожится». Ничего не понимает, в глазах ужас. Я продолжаю: «Мы должны решить уравнение относительно у, да? »

– Нужно же было относительно х решать, ну зачем ты «у» написал?

У меня случился затык, не могу объяснить и всё. И тогда я по­нял, что из меня получается очень плохой учитель. Я привык го­ворить со школьниками, которые приходили на маткружок. А они не задавали таких вопросов.

Спустя годы я закончил мехмат МГУ и Российскую Экономи­ческую Школу (РЭШ), после чего ездил по регионам России, вел курсы повышения квалификации для преподавателей экономики. В Москве считалось, что экономика – наука совершенно матема­тизированная и точная. По крайней мере, и в РЭШ, и в Высшей Школе Экономики до сих пор всячески насаждается, что мате­матика – это главное в экономике. В регионах мы столкнулись, однако, с преподавателями, которым было трудно перешагнуть че­рез вещи, для математиков очевидные. Но через пять дней курса многие слушатели оказывались очень способными к математике. Просто в некотором месте у них стоял заслон. Его полезно пре­одолеть всем, ибо это – часть интеллектуальной культуры. Да­же если вы никогда не занимались математикой, некоторые вещи знать надо... Так же как я должен знать что‑ то про историю или химию.

Давайте теперь поговорим о словосочетании «абсолютное дока­зательство». Если вы в общем и целом поймете, что это такое, то значит, мы не зря сегодня позанимались с вами.

Что такое абсолютное доказательство, я объясню на примерах. Начнем с игры в «пятнадцать».

 

Слушатель: Пятнашки?

Слушатель: Шестнашки?

А. С.: Чтобы мы говорили об одном и том же, я объясню пра­вила этой игры.

В квадрате 4x4 имеется пятнадцать одинаковых квадратных фишек, пронумерованных от 1 до 15. Их нельзя вынимать, мож­но только передвигать на свободное место. Стандартная исходная позиция: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 и пустое ме­сто, которое используется для передвижения фишек. (См. рис. 1; может быть задана и нестандартная исходная позиция. )

 

Пустое место можно гнать по всей игровой зоне, т. е. разрешен­ное действие при игре – передвижение на пустое место одной из соседних с ним фишек.

Игру придумал где‑ то 130 лет назад американский математик‑ популяризатор Сэм Лойд. А чуть позже он пообещал большой приз

Такая вот детская игра. Делайте, что хотите (в рамках ука­занного правила). Передвигайте фишки как вам угодно. Только приведите игру в исходную позицию. Начался настоящий пятна‑ шечный бум. Примечательно, что на этот момент наука алгебра в другой части света находилась в очень продвинутом состоянии. Математики сказали свое веское слово, предоставив абсолютное доказательство того, что выиграть в такую игру невозможно. Тем не менее ажиотаж с игрой в пятнашки продолжался еще много лет – так много было желающих посрамить математику и «сру­бить» тысячу долларов.

 

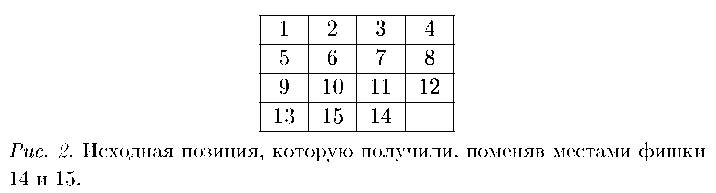
($1000) тому, кто переведет комбинацию с картинки рис. 2 в исход­ную позицию на рис. 1.

Что же означает в этой игре «абсолютное доказательство»? Это значит: какие бы действия вы не совершили, сколько бы времени и каким количеством способов бы не передвигали фишки, вы ни­когда, ни при каких условиях не вернетесь из позиции на рис. 2 в исходную позицию на рис. 1. В частности, если кто‑ то предъявил такое решение, значит он – лгун. Он, видимо, взял, выдрал фиш­ки из коробки и расставил их в правильном порядке. Абсолютное доказательство – это точное, настолько точное утверждение, на­сколько вообще что‑ то может быть точным. Математика – наука точных утверждений. Не «примерно», не «может быть», не «скорее всего, не приведете», а никогда, ни при каких условиях не приве­дете, какие бы способности к этой игре у вас ни были.

Я постараюсь доказать эту теорему. Но что значит «постараюсь доказать»? Что вообще означает «доказать»? Что значит «я ее докажу»? Как вы это понимаете?

Слушатель: Мы будем убеждены.

А. С.: Вот именно. Я найду способ вас убедить. Но с другой стороны, это не совсем то, что нам нужно.

Расскажу такую историю. Один рыцарь объяснял другому ры­царю математику. Первый рыцарь был очень умный, а второй – очень глупый. Второй рыцарь никак не мог понять доказательство. И тогда умный рыцарь говорит: «Честное благородное слово, это так». И второй сразу поверил: «Ну, тогда о чем разговор. Мы же с Вами люди безупречной чести, и я, конечно, Вам верю. Я полно­стью убежден».

У нас разговор пойдет не о таком способе убеждения. Идея ма­тематического, абсолютного доказательства не в том, что я дам честное слово, а в том, что я, апеллируя к вашему разумению, передам вам какое‑ то знание, которое вы потом столь же спокой­но передадите дальше. Вы придёте и скажете: «Мы знаем, поче­му в “пятнашки” бессмысленно играть. Мы это знаем совершенно точно, нам это доказал Алексей. И не просто доказал при помощи какого‑ то там шаманства, пошаманил‑ пошаманил и сказал, что нет решения у этой задачи. Мы получили такое знание, которое смо­жем воспроизвести и доказать, что выиграть в игру “пятнашки” невозможно».

Насчет пошаманить есть очень поучительный эпизод из жиз­ни математиков. В начале XX века жил в Индии математик Сри­ниваса Рамануджан. На момент начала нашей истории ему было 26 лет. Он заваливал письмами лондонское математическое обще­ство, в которых были формулы, содержащие числа «7Г» и «е» (мы с ними позже познакомимся) и страшные бесконечные суммы, ко­торым эти выражения равны. В Лондоне проверяют – всё верно. А Рамануджан присылает всё новые и новые письма. Профессор математики Г. Харди приглашает его приехать в Англию и рас­сказать, как он выводит эти формулы. Рамануджан отвечает, что формулы сообщает ему во сне богиня Маха‑ Лакшми1. Харди, ко­нечно, посмеялся, решив, что индус не хочет делиться секретом.

Английский математик пишет новое письмо, в котором пытается заверить Рамануджана, что никто не будет претендовать на его открытие. Такое предположение оскорбляет индуса. Он отвечает, что совершенно не дорожит такими вещами, как авторство.

В конце концов Рамануджан все‑ таки приехал в Лондон, где стал профессором университета. Многие присланные им формулы оказались верны. Но далеко не все из предложенных им формул на сегодняшний день доказаны. Некоторые из них остаются от­кровениями, которые были сообщены богиней Рамануджану. «Аб­солютное» их доказательство пока неизвестно.

А теперь отдохнем, посмотрим на этот футбольный мяч (рис. 3).

 

Из чего состоит мяч? Он сшит из лоскутков. Вы когда‑ нибудь задумывались над том, как именно сделан футбольный мяч и по­чему именно так? Это чисто математический вопрос. Вы пока подумайте, где же тут математика. А я приступаю к математиче­скому доказательству невозможности выиграть в игру «15».

Начнем с гораздо более простой ситуации. Возьмем доску 8x8 (рис. 4) и достаточно большой запас (заведомо больший, чем нам может понадобиться) костей домино (одна доминошка покрывает две клеточки на доске).

 

Теперь я аккуратненько отрезаю у квадрата 8x8 два проти­воположных угла (рис. 5). Получилась фигура, которая состоит из 62 квадратиков. Число, делящееся на 2. Поэтому почему бы не попробовать замостить ее доминошками. Но если вы начнете пытаться сделать это один, два, три, четыре раза, у вас ничего не будет получаться. 30 доминошек влезет, а 31‑ я нет. Физик, когда увидит эту ситуацию, поэкспериментирует 1000 раз и ска­жет: «Экспериментально установлен закон нарисованная фи­гура не замощается доминошками 1 х 2». Физик2 также может наблюдать за игрой в футбол много‑ много раз и сказать: «Экс­периментально установлено, что мяч падает вниз, а также, знаете,

все остальные тела, похоже, тоже падают вниз». Все знают, что все тела падают вниз. Это экспериментальный факт. Но доказать этот факт, в принципе, невозможно. Никто на свете не гаранти­рует, что завтра этот закон не прекратит действовать. Придумают какую‑ нибудь гравицапу, и всё полетит не вниз, а вверх. Это – фи­зический закон, он не может быть доказан. Он может быть только проверен очень много раз. Еще хуже с социальными и экономиче­скими законами, например, с законом «спрос рождает предложе­ние». У экономистов много таких заклинаний. И они очень часто не работают. Наступает кризис, наступает новая фаза развития социума – и всё. Перестают быть верными старые законы. Соци­альная реальность постоянно ломает стереотипы, которые связа­ны с ее поведением, развитием, эволюцией. Физическая реальность так не делает, но тем не менее доказательств в ней тоже нет.

В нашем случае с доской мы, в принципе, можем попробо­вать перебрать все варианты и сделать вывод – не получилось. Но сколько времени нам нужно будет потратить? Давайте при­мерно оценим. Сколькими способами можно положить первую до­миношку?

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: