Слушатель: Тремя. Слушатель: Двумя. Слушатель: Тридцатью. Слушатель: Кучу.. А.С.: Ничего не выйдет. Общая площадь 62, у каждой фишки 2, значит нужна 31 доминошка, это мы понимаем. Но 30 умещается, а 31 нет (рис. 6).

Слушатель: Тремя.

А. С. (показывая на доске 8x8 различные положения кости домино): Раз, два, три, четыре, пять, шесть, семь, восемь, девять...

 

Слушатель: Двумя.

Слушатель: Тридцатью.

А. С.: Ну, тридцатью – хорошо. А почему двумя?

Слушатель: Вертикально и горизонтально.

А. С.: Это два способа ее расположения. А сколько положений на самой доске она может занять?

 

Слушатель: Кучу.

А. С.: Очень‑ очень много. 30 – это довольно хороший ответ. На самом деле около 50. Давайте исходить из 50. На самом де­ле не важно, что 30, что 50, даже 10. Потому что после того как мы положили первую такую фишечку, сколько способов остается для второй?

Слушатель: (п‑ 1).

А. С.: Грубо говоря, 49. Еще, на самом деле, надо учесть поря­док, в котором мы положили доминошки. Нужно поделить на два. То есть 50 умножим на 49 и поделим на два.

Дальше кладем третью, четвертую и так далее. И каждый раз домножаем и домножаем – количество вариантов очень быстро растет. (Показывает на доске всё новые варианты. )

 

Есть миф, будто математика состоит из формул. В 1993 го­ду, когда я учился на 3‑ м курсе мехмата, я ехал на Урал к тете. Со мной в купе ехала мама с маленькой 4‑ летней дочкой. И дочка говорит: «Мам, а, а можно почит, ат, ъ дядину книгу? » Книга м, оя называлась «Алгебра». Мама сказала: «Ты в ней ничего не пой­мешь, там одни формулы». Я передаю книгу и говорю: «Найди­те первую формулу. На какой она странице? » Формул в книге по алгебре не очень много, и самое страшное не в их количестве, а в том, что они ужасающие, в них одни буквы, даже цифр почти нет. Это, скорее, похоже на какой‑ т, о древний язык. Совершенно не то в книге, что должно быть с точки зрения людей. Идея, что математика состоит из формул, столь же чудовищна, как мысль, что в храм люди заходят, чтобы просто совершить обряд, поставить свечку. Моя дочь говорит, например: «Пойдем,, поста­вим огоньки». Для нее это нормально, она маленькая. Матема­тика – это вселенная, в которой есть язык формул. Но суть не в нём, а в том, какие глубинные законы есть в математи­ке. И вот эти законы, эту внутреннюю красоту я постараюсь вскрыть.

После такого философского отступления вернемся к нашей доске.

Произведение, которое получится уже через 20 умножений, име­ет порядок количества атомов во вселенной (как любят говорить в научно‑ популярных книгах). Вот с чем сравнимо количество спо­собов, которые нужно перебрать, чтобы заявить: «Мы перебрали все варианты, задачу решить нельзя». Надо придумать что‑ то дру­гое. И то, что мы сейчас придумаем это абсолютное доказатель­ство.

Может быть, у кого‑ то есть идеи?

Слушатель: Взять площадь каждой фишки и разделить на нее общую площадь поля.

А. С.: Ничего не выйдет. Общая площадь 62, у каждой фишки 2, значит нужна 31 доминошка, это мы понимаем. Но 30 умещается, а 31 нет (рис. 6).

 

Последняя доминошка распадается на два квадратика в разных местах. И что бы вы ни делали, последняя будет, как заколдован­ная, распадаться на два квадратика.

Теперь я доказываю, что замостить доску доминошками невоз­можно.

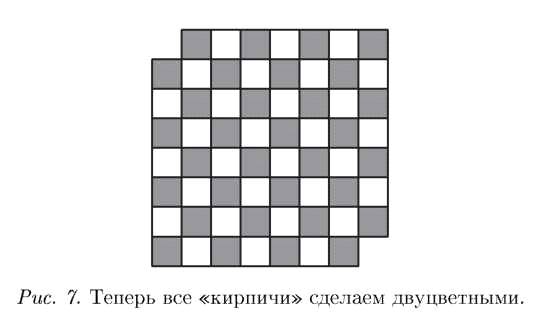
Ведь перед нами, по сути, шахматная доска. Давайте вернем ей ее шахматный вид. Клетки на ней будут то черные, то белые (рис. 7).

После вырезания двух угловых квадратиков, сколько черных и сколько белых клеточек останется?

Слушатель: Одних будет больше, других меньше.

Слушатель: Одна доминошка должна покрывать и белую, и черную, да?

А. С.: Кто‑ то уже всё понимает (см. рис. 8). Любая доминош­ка, уложенная на эту доску, покрывает и белую, и черную клет‑

 

 

 

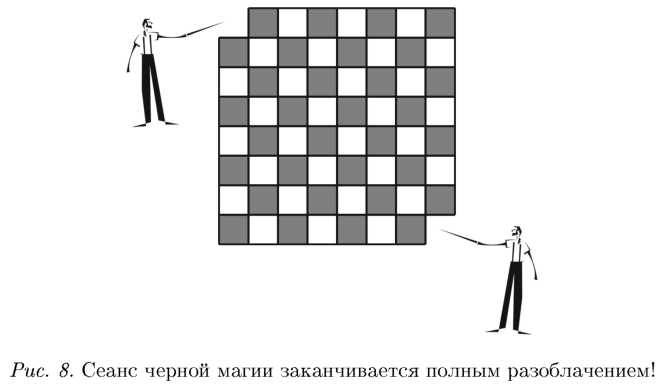
ку. Поэтому, если бы фигуру, которую я сейчас нарисовал, можно было бы заложить доминошками, черных и белых клеток было бы одинаковое количество. Но мы вырезали две белых. Осталось 30 белых и 32 черные клетки. Противоречие. Количества черных и белых клеток не равны друг другу. Значит, нашу фигуру нельзя замостить доминошками. Абсолютное доказательство закончено. Не надо ничего перебирать.

Повторю еще раз.

Я взял урезанную с двух сторон шахматную доску. Исходная шахматная доска имела 32 черные и 32 белые клетки. А в урезан­ной шахматной доске пропали две белые угловые клетки. Поэтому стало 30 белых и 32 черных. Теперь предположим на секундоч­ку, что мы решили задачу, и все клетки заполнены доминошками. Следует заметить, что каждая доминошка обязана лежать одной своей половиной на черной, а другой своей половиной на белой клеточке, как ты ее ни клади. Следовательно, если бы мы смогли замостить эту фигуру доминошками в количестве 31 штуки, то бы­ла бы 31 черная и 31 белая клетка. У нас же 32 черные и 30 белых клеток. А значит, замостить обрезанную доску нельзя. В этом и со­стоит препятствие, как говорят математики, препятствие к реше­нию задачи. Заметьте, что мы проводили доказательство от, про­тивного. Это очень важный прием. Я предположил, что мы задачу решили, и привел ситуацию к явному противоречию.

Переходим к более сложному сюжету – «разоблачению игры в пятнадцать».

Сейчас вы узнаете тайну, которую почти никто не знает: почему в пятнашки нельзя «выиграть», то есть перевести игру из позиции на рис. 2 в исходную позицию на рис. 1. Посмотрим на измененную позицию:

 

Глядя на рис. 9, выпишу числа от 1 до 15 в линеечку, но не под­ряд, а хитрым способом. Зачем я это сделаю, будет ясно потом. Вот они:

1, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 14, 15, 13.

Такой порядок движения древние греки называли «бустрофедон», что в переводе значит «так, как пашет бык» (рис. 10).

 

С помощью такого движения я закодировал информацию об игровом поле в виде одной строки. Обратно раскодировать так же просто, как и закодировать (с : точностью до нахождения пустого места).

Если, например, сдвинуть 14 в угол, то при кодировании я по­лучу такую же строчку (см. рис. 11). Вообще, легко понять, что правила игры «15» позволяют быстро и уверенно перегнать пустое место на игровом поле на любую клетку из шестнадцати, двигаясь бустрофедоном.

Примечание. Кодированием называется процедура изображе­ния элементов одного множества с помощью элементов другого (обычно более простого) множества, желательно таким образом, чтобы не потерялась никакая существенная часть информации

о первом множестве.

 

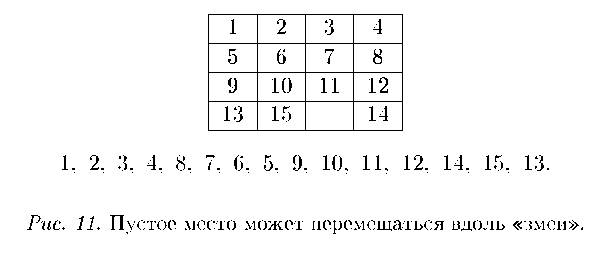
При этом если пустое место находилось где‑ то в другом месте, в середине, например, то всегда можно передвинуть фишки так, чтобы оно оказалось в конце.

Теперь мы, начиная с положения рис. 9, должны каким‑ то обра­зом менять это положение, гонять пустое место, чтобы прийти к последовательности, соответствующей рис. 1:

1, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 15, 14, 13.

Каждый раз, когда я переставляю пустое место, наша строка ме­няется. Я хочу показать, что как бы она ни менялась, кое‑ что со­храняется. В математике это называется словом инвариант.

Инвариант – что‑ то, что не меняется.

Понятие инварианта – одно из ключевых математических по­нятий.

Итак, есть что‑ то, что связано с нашей последовательностью, что при выполнении разрешенных действий не будет меняться. Что это, угадать так просто нельзя, иначе миллионы людей в Америке и в Европе не занимались бы ерундой.

В процессе перестановок строка будет сильно меняться, вплоть до очень серьезного перемешивания. Но что‑ то меняться не будет никогда. Давайте напряжемся и поймем, что это такое.

Рассмотрим все пары чисел (чисел всего 15). Сколько всего можно составить пар?

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: