Слушатель: Понятно. Слушатель: А. Слушатель: Да.. Врезка 3. Еще одно упражнение для слушателей. Ниже описано странное путешествие неких космических Магел­ланов. Могло ли такое быть в космосе?

Слушатель: Понятно.

Слушатель: А как взаимосвязаны картинки на торе и шаре?

А. С.: То есть как именно они друг с другом соотносятся? Ни­как. Каждая из картинок, независимо друг от друга, является как бы «сетью», наброшенной на данную поверхность. Эту сеть при же­лании можно сделать состоящей из треугольных ячеек. Тогда она называется «триангуляцией поверхности».

Слушатель: А не может быть такого, что будет то же самое количество вершин, ребер и граней, но при этом картинка будет другая?

А. С.: Смотря, что понимать под словом «другая». Она может, безусловно, немного иначе выглядеть: ребра могут быть длиннее или короче. Но мне достаточно того, чтобы имелось то же самое количество вершин, ребер и граней. А при изгибах, растяжениях и сжатиях поверхности это будет именно так.

 

Слушатель: А...

А. С.: Итак, если вы поверили, что не изменится ни количе­ство вершин, ни количество ребер, ни количество граней, то всё остальное я докажу совершенно строго. Я продемонстрирую, что величина В – Р + Г на шаре и на торе разная: на автомобильной камере она равна 0, на сфере – равна 2.

Слушатель: А если предположить, что дырка у тора имеет площадь ноль. По‑ прежнему число Эйлера – О?

А. С.: А что значит «площадь дырки»? Это значит, что бублик сходится в одной точке – в серединке?

 

Слушатель: Да.

А. С.: Нет, эйлеров индекс В^Р + Г будет другой. Фигура, кото­рая получится, не устроена как обычная плоскость в окрестности любой своей точки, потому что в окрестности серединки, где дырка сходится с разных сторон, она устроена очень сложно.

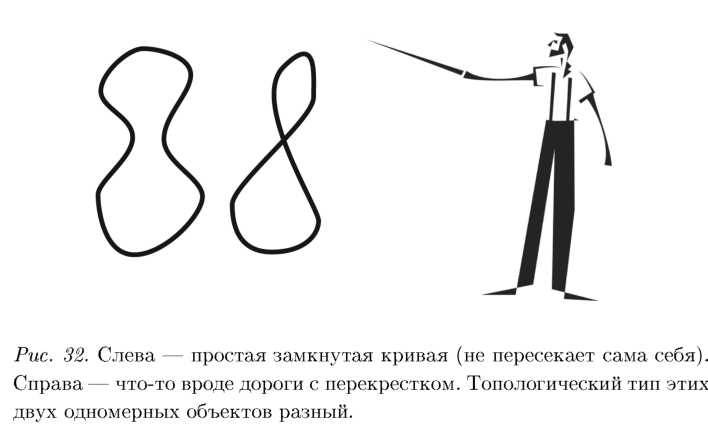
Чтобы понять это, рассмотрим сечение тора (с заклеенной ды­рой) вертикальной плоскостью, проходящей в стороне от точки за­клейки, а также плоскостью, проходящей через точку заклейки. Рассмотрим две замкнутые кривые, получившиеся в сечениях (см. рис. 31).

Первая кривая устроена как окружность, окрестность любой ее точки – просто интервал, а вторая кривая устроена иначе (рис. 32). Потому что в любой микроскоп окрестность точки пе­ресечения видится как крест, а не как отрезок. То же самое с то­ром – с автомобильной камерой. С точки зрения таракана, кото­рый по ней ползает, это просто плоскость (если, конечно, дырка

 

в торе но была заклеена). Но и шар с точки зрения таракана тоже плоскость (ведь он в каждый момент времени видит только маленький кусочек «у себя под носом», а он почти плоский). То есть смотрите, что происходит. Таракан, который ползает по то­ру и по шару, не может понять, что это разные объекты. Мы та­кие же тараканы, мы живем в трехмерном пространстве, мы трехмерные тараканы. Мы знаем, что вокруг нас есть окрестность. Окрестность это обычное трехмерное пространство: его опреде­ляют 3 взаимно перпендикулярных оси. То есть я вижу трехмер­ную окрестность вокруг себя, но я не знаю, как устроена вся все­ленная целиком. Я не могу иметь такого представления. Так вот: топология приоткрыла эту тайну. Гипотеза Пуанкаре как раз про то. как устроено пространство, где мы живем. Мы видим, что во­круг нас всё трехмерно, но мы не знаем внутри какого рода объекта мы живем. То ли мы живем в обычном бесконечном трехмерном пространстве, то ли мы живем на поверхности трехмерной, изви­ните. сферы, которая ограничивает четырехмерный шар. Не мо­жем мы этого понять, просто посмотрев вокруг себя. Ведь радиус такой «трехмерной сферы» может равняться, скажем. 100 милли­онам световых лет. А на такие расстояния глаз посмотреть не спо­собен.

 

 

Врезка 3. Еще одно упражнение для слушателей. Ниже описано странное путешествие неких космических Магел­ланов. Могло ли такое быть в космосе?

... Вех; астрономы Земли в 3333 году нашей эры были в глубо­ком недоумении. Один из них. направляя свой телескоп в разные точки небесной сферы, имел привычку фотографировать не толь­ко ее. но и (перейдя в другое полушарие Земли), фотографировать также диаметрально противоположную ей точку. Накопив изряд­ное количество таких пар фотографий, он принялся их изучать. И вдруг сюрприз: на одной из двух фотографий пары он увидел маленькое, но вполне различимое созвездие в виде правильного пя­тиугольника. Велико же было его изумление, когда на другой фо­тографии пары он увидел ТАКОЕ ЖЕ созвездие, той же величины и той же яркости! Велико было и удивление всех остальных астро­номов. когда они услышали это сообщение (и немедленно провери­ли его). И скоро об этом узнали все жители Земли. Было решено одновременно выслать две космических экспедиции (на предмет проверки, не посылают ли на Землю сигналы внеземные цивили­зации): одна экспедиция – прямо в центр первого пятиугольника, вторая – в центр диаметрально противоположного пятиугольни­ка.

Долго летели космонавты в ту и в другую сторону с одинаковой «субсветовой» скоростью – целых 10 лет. И всё это время за их ракетами наблюдали чуткие приборы астрономов. Вдруг в центре первого 5‑ угольного созвездия была зафиксирована яркая вспыш­ка неправильной формы, и первая ракета ИСЧЕЗЛА. Астрономы решили взглянуть, видна ли вторая ракета. К своему ужасу, они увидели, что ровно в тот же момент с диаметрально противопо­ложной стороны была зафиксирована вспышка ТОЙ ЖЕ ФОРМЫ, и вторая ракета тоже исчезла.

Могло ли такое быть?

 

ОТВЕТ. Могло. Если бы только космос, в кот, орый погружена Земля, был не бесконечным трехмерным пространством, а очень большой, по конечной трехмерной сферой.

Чтобы лучше понять это, представьте себе, что наша Земля сплошь покрыта мировым океаном, на котором имеется (на эква­торе) только один небольшой остров вроде Крита. Поверхность этого океана является двумерной сферой, но свойства у нее по­хожи на свойства трехмерной сферы. И выплыли с этого острова два одинаковых корабля (в один и тот же момент времени): один поплыл ровно на запад, другой – ровно на восток. Плыли они быстро и потому очень сильно столкнулись (в точке, диаметраль­но противоположной острову Криту). От столкновения они могли взорваться. После отплытия прочие люди следили за ними, посы­лая вслед радиоволны (а они, как известно, могут огибать поверх­ность Земли). На экране радара и на западе, и на востоке всё вре­мя был виден какой‑ то странный правильный пятиугольник (ока­залось, что это – радиомаяк из пяти источников, построенный кем‑ то на противоположной точке поверхности Земли). Корабли взорвались как раз в центре этого пятиугольника. Взрыв был за­фиксирован одновременно и западным, и восточным радаром.

Сверху из нашего трехмерного мира мы видим, что тор и сфе­ра – разные объекты. Но глазами червя, который ползает по дву­мерной поверхности, этого не видно, всё одинаковое. Вопрос: как же доказать червю, что поверхности разные?

Допустим, что у червя есть мышление, он может воспринять ма­тематическое рассуждение. Как я могу передать ему знание? А вот как. Я ему говорю: «Ты можешь, экспериментально исползав сфе­ру, проверить, сколько здесь вершин? » Он говорит: «Ну, конечно могу. Я постепенно все их обползаю, поставлю метку, найду алго­ритм, которым я посчитаю количество вершин». Тогда я спрошу: «Можешь ли ты посчитать количество ребер? » – «Ну, конечно, могу», – говорит он. «А граней? » – «Тоже могу. Нет проблем ни­каких. Каждый раз переходя из грани в грань, заливаю ее водой. В следующий раз я к ней приду, а она уже мокрая, значит, я ее уже посчитал». Понятно, что, находясь на двумерной поверхности, не выходя в трехмерное пространство, можно посчитать, сколько ребер, вершин и граней. Теперь, если я пересажу червя на тор, он посчитает вершины, грани и ребра и убедится, что индекс Эй­лера имеет другое значение. На сфере – 2, а на торе – 0. Тут я ему и скажу: «Теперь ты понимаешь, что поверхности абсолют­но разные, они с нашей человеческой трехмерной точки зрения абсолютно разные. Они с твоей точки зрения одинаковые, потому что ты видишь локально, а с нашей трехмерной – они разные». То же самое происходит с нашей трехмерной вселенной, с точки зрения четырехмерного пространства. Наше пространство может быть устроено по‑ разному, но Г. Перельман доказал теорему, ко­торая ограничивает класс того, что нам нужно проверять, когда мы выясняем, где живем.

Слушатель: А как Эйлер пришел именно к этой формуле?

А. С.: Честно говоря, я не знаю, но он вообще был гений. Го­ворят, что у него никогда не было математических ошибок и не­верных утверждений. Даже не совсем обоснованные рассуждения Эйлера (после их очевидной коррекции) были впоследствии под­тверждены. Видимо, он настолько верно чувствовал ситуацию, как будто внутри него находился «барометр правильности», с которым он постоянно сверялся.

Математика это прозрение. Вы идете но парку, вокруг листья шелестят, бах и вы всё поняли. Это не от вас, это как бы сверху идет.

Сейчас я буду доказывать, что на сфере индекс Эйлера равен

а на торе он равен 0, и, может быть, вам будет ясно, как Эйлер к этому пришел.

 

Рис. 33. Накидываем «сеть» из ребер и вершин на верхнюю половину сферы и на небольшой кусок поверхности тора. Нижняя часть сферы может трактоваться как одна гигантская грань (грани не обязательно должны быть треугольными). Оставшийся кусок тора НЕ МОЖЕТ счи­таться «гранью», так как грань не может выглядеть как трубка. Надо эту трубку подразбить на более мелкие части (на треугольники, квадратики и т. д. ).

Допустим, я уже сформировал «сеть», покрывающую сферу, и «сеть» для тора (рис. 33).

Стираю одно ребро на сфере (потом буду стирать ребра и на то­ре). Что меняется вот в этом нашем выражении (то есть В^Р + Г)?

Слушатель: Минус одно ребро.

Слушатель: Минус одна грань.

А. С.: Значит, выражение В – Р + Г не изменилось (рис. 34).

Какие еще операции я могу сделать с этой картинкой? Могу убрать еще одно ребро. Опять ничего не изменится. Но в какой‑ то

 

момент меня ударят но рукам. Некоторые вершины могут стать странными (что‑ то вроде куска забора в чистом поле).

Может получиться «висячая вершина» она связана с един­ственным ребром (может быть и несколько таких кусков, см. рис. 35).

 

Давайте превратим вот такое ребро во что‑ нибудь человеческое (только не в человеческое ребро! ). Что для этого надо сделать?

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: