Врезка 1. Упражнение для слушателей (необязательное; но ответ полезно прочесть)

Лекция 2

А. С.: Сегодня мы займемся тем, что называется топологией. Многие считают ее центральной наукой в математике. Математи­ка – это центральная наука во всех науках. Топология получает­ся тогда как бы «центром внутри центра», то есть самой главной дисциплиной. Она сформировалась в начале XX века, и постепен­но стало ясно, что она лежит в сердце математики. На простом языке, топология – это геометрия плюс анализ. А можно ска­зать и по‑ другому: тот, кто хочет понять самые глубокие и важные закономерности и геометрии, и математического анализа, должен изучать эти науки с топологической точки зрения.

100 лет назад топология уже достаточно хорошо оформилась, а началась она, наверное, с Эйлера (того самого Эйлера, фор­мулу которого мы сегодня будем с вами изучать). Были сфор­мулированы определения важнейших объектов топологии: линия, поверхность, объём, многомерное прост, ранет, во. Было осознано, что у топологических объектов имеется важное свойство: раз­мерность. Например, линия – это одномерный объект (его мож­но при этом поместить в 1‑ мерное пространство, в 2‑ мерное, в 3­мерное и даже в так называемое «4‑ мерное пространство»). По­верхность – двумерный объект (он может располагаться в 2­мерном пространстве, в 3‑ мерном, 4‑ мерном и так далее). Тело, имеющее положительный объём – это 3‑ мерный объект; но оно может располагаться в 3‑ мерном, 4‑ мерном, 5‑ мерном... простран­ствах. Ниже всё это будет рассматриваться в самых простых случаях, поскольку свойства топологических объектов, лежащих в 4‑ мерном, 5‑ мерном, 6‑ мерном... пространствах недоступны не­посредственному геометрическому восприятию человека. Может быть, это хорошо, что человек не может совершить даже неболь­шую и короткую по времени прогулку в «подлинное» 4‑ мерное про­странство. Вернувшись из такой прогулки, этот бедняга мог бы с ужасом обнаружить, что сердце у него теперь находится не с ле­вой, а с правой стороны (и ему, кроме того, придется примириться с тем фактом, что он стал левшой, хотя ранее им не был). Так

что с 4‑ мерным пространством шутки плохи. Но и в 3‑ мерпом про­странстве (казалось бы, так хорошо нам знакомом) топология су­мела обнаружить ряд совершенно сногсшибательных фактов. При­ступим же к ее изучению (конечно, на общеописательном уровне, не достигая стопроцентной строгости изложения).

Допустим, у вас есть глобус, или футбольный мяч, или арбуз. Это объекты по сути разные, а по форме они одинаковые. Как гово­рится на житейском языке, это тела, которые имеют форму шара. Однако с точки зрения топологии арбуз резко отличается от гло­буса и от футбольного мяча: арбуз внутри заполнен веществом, а глобус и мяч внутри пустые. Разумно считать, что толщина кар­тонной поверхности глобуса и толщина оболочки мяча имеют ну­левую толщину. Тогда глобус и мяч являются двумерными объек­тами, а арбуз – трехмерным. Но можно мысленно рассматривать поверхность арбуза – получится «двумерный объект, ограничи­вающий исходный трехмерный арбуз». Ниже мы будем говорить просто о поверхности шара (неважно, какого диаметра). Допустим, что мяч имеет диаметр 20 см, поверхность арбуза – диаметр 50 см, а глобус – 200 см. Для лучшего понимания, что такое топология, рассмотрим также кубик со стороной 20 см, склеенный из бума­ги, и таких же размеров кубик, сделанный из кусочков проволоки, идущих вдоль ребер куба. Итого у нас имеется пять объектов. С об­щежитейской точки зрения их можно разделить на две группы – «круглые» (3 шт. ) и «кубообразные» (2 шт. ). С точки зрения чело­века, привыкшего всё измерять сантиметром (например, портного), их надо разделить на две группы по другому принципу: «предме­ты с размерами порядка 20 см» (3 шт. ) и «более крупные предме­ты» (2 шт. ). А с точки зрения математика‑ тополога, здесь имеют­ся четыре абсолютно одинаковых предмета и один особенный (а именно, проволочный куб). И тополог даже даст обоснование, почему он так считает: первые четыре объекта являются двумер­ными, а последний объект – одномерный. Таким образом, тополо­гия не только не видит разницы между поверхностью шара диаме­тра 20, 50 или 200 см, по и не видит, разницы, между поверхностью куба и поверхностью шара! Итак, тополог надевает на себя «вол­шебные очки», которые не позволяют определить ни размеры, ни форму предметов. Что же он тогда через них сможет разглядеть? Он сумеет разглядеть самое глубинное отличие представленных ему предметов друг от друга, их, так сказать, конструкцию. На­пример, добавим к этим пяти предметам еще и бублик с внешним диаметром 20 см и будем интересоваться не самим бубликом, за­полненным тестом, а только его поверхностью. А также добавим обыкновенное кольцо из проволоки (диаметром 1 см). Что скажет тогда тополог? «С точки зрения размерности здесь имеется два типа объектов: двумерные и одномерные. Но поверхность бублика резко, принципиально отличается от поверхности шара. Точно так же проволочный кубик резко отличается от кольца из проволо­ки. Итак, здесь представлены четыре различных топологических типа: поверхность шара (4 предмета), поверхность бублика, окруж­ность, проволочный кубик».

Врезка 1. Упражнение для слушателей (необязательное; но ответ полезно прочесть)

Во времена фашистской Германии в ней процветали ученые‑ шарлатаны. Один из них на полном серьезе утверждал, что всё космическое пространство вокруг Земли заполнено... льдом. (То есть, что мечтать о космических полетах бессмысленно. ) Ну, до­пустим, это так и есть. Хм. Рассмотрим тогда три объекта: по­верхность Земли, внутренность Земли и наружная часть Земли, состоящая, хм, изо льда. Как называются эти объекты на языке топологии? Одинаковы ли с точки зрения топологии второй и тре­тий объект?

ОТВЕТ. Первая часть ответа: первый объект – двумерный, типа сферы. Не имеет граничных точек.

Второй объект: 3‑ мерный, типа шара. Его граничные точки – все точки поверхности Земли.

Третий объект: 3‑ мерный, типа шарового слоя. Граничные точ­ки – все точки поверхности Земли.

Вторая часть ответа: второй и третий тип топологически раз­личны, так как шаровой слой существенно отличается от шара. Граничные точки у них тем не менее одинаковы.

Третья часть ответа: не следует говорить, что третий объ­ект «бесконечный по размерам», так как в топологии неважно, каковы размеры объектов. Например, если взять поверхность сфе­ры и выкинуть из нее одну‑ единственную точку, то по житейским представлениям этот объект «конечный по размерам», в то вре­мя как плоскость «бесконечна». По правилам же топологического исследования, сфера с «выколотой» точкой имеет тот же тополо­гический тип, что и плоскость.

Возьмем и изогнем, изомнем, растянем поверхность шара, но нигде не порвем;, и не склеим, никакие две точки в одну. Мы можем из нее таким образом получить, например, куб (то есть, естествен­но, не сам куб, а его поверхность). Чтобы понять, как это дела­ется, покажем, как из круга, изготовленного из резины, получить квадрат (размеры квадрата неважны). Для этого надо в четырех равноудаленных местах границы круга потянуть наружу резино­вый слой, пока он не примет форму квадрата. В частности, точки границы круга превратились в точки периметра квадрата.

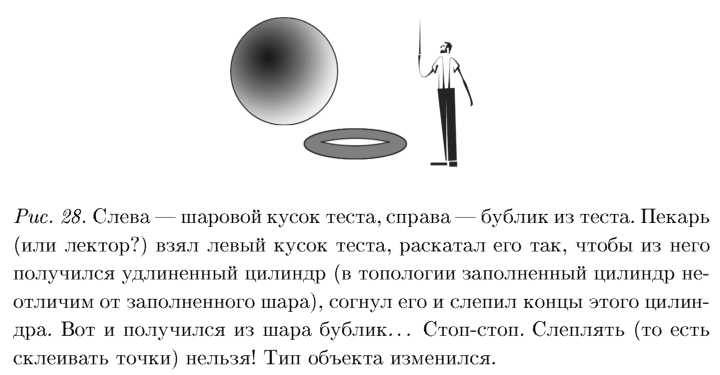
Можно много чего сделать из резиновой камеры сдутого фут­больного мяча. Но есть интуиция, которая подсказывает, что ав­томобильную (или велосипедную) камеру из камеры футбольного мяча сделать будет затруднительно, даже используя те широкие возможности, которые предоставляет нам топология. Куб, элли­псоид (то есть сжатая поверхность сферы), яблоко, арбуз – по­жалуйста, а вот бублик из шара не сделаешь, не порвав его, либо не склеив между собой некоторые точки. Согласно сказанному вы­ше, надо различать две разные задачи: 1) Из заполненного шара сделать заполненный бублик и 2) Из поверхности шара сделать поверхность бублика. Первая задача «решена» в подписи к рис. 28.

И Эйлер задался вопросом, а можно ли это утверждение дока­зать? Вроде бы интуитивно оно совершенно понятное. Но матема‑

тика ставит задачу перевести очевидное на язык строго доказанно­го. Ведь если мы откроем цивилизацию, которая, например, живет на плоскости, для ее жителей будет не очевиден рассматриваемый нами факт (см. врезку 2). А с номощыо математики мы сможем передать им содержание теоремы. К чему я клоню?