Слушатель: 7.. Слушатели: 14.

Слушатель: 7.

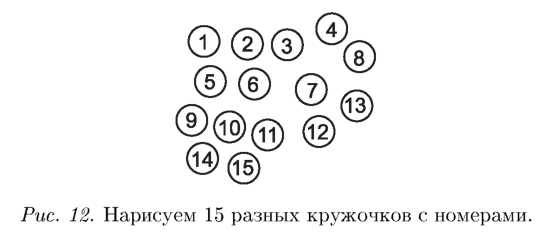
А. С.: Нет. Всех различных пар. Пусть у нас есть 15 кружочков разного цвета. Сколько существует способов вынуть два кружка?

Пока будем считать, что порядок, в котором мы вынимаем кру­жочки, нам важен. Сколькими способами я могу взять первый кру­жок?

Слушатель: Пятнадцатью.

А. С.: Пятнадцатью. Правильно.

Слушатель: 15 факториал?

А. С.: Нет. 15 факториал – это множество всех возможных строк.

 

Но водь гуманитарии но обязаны знать слово «факториал», о ко­тором мы с вами говорим. Термин «факториал» нам понадобится в других томах, поэтому я ого определю.

Есть некоторое число п. Простите, я употреблю буковку. Умно­жим п на п –1, потом на п^2 и так далее, и. наконец, умножим на 2 и на 1. То. что получилось, обозначается п! (это и есть факториал числа п):

п! = п · (п – 1) · (п – 2) ·... · 2 · 1.

Например. «15 факториал»:

15! = 15‑ 14‑ 13‑ 12‑ 11‑... ‑ 2‑ 1.

Слушатель: Мы сейчас что‑ то прояснили?

А. С.: Нет. Было произнесено слово «факториал». И теперь я его объясняю.

Факториал это произведение подряд идущих, убывающих до единицы натуральных чисел. В нашей задаче он не понадобится (понадобится в другой лекции).

Первый кружок вы можете выбрать 15 разными способами. Сколько остается способов для выбора второго кружка?

 

Слушатели: 14.

А. С.: 14. Итого? Есть такое знаменитое правило произведения. Число способов выбрать пару это произведение количества спо­собов выбрать первый ее элемент на количество способов выбрать второй. Почему? Мы выбрали первый. Посмотрим, сколько пар мы с ним можем получить. Второй выбирается 14 способами, значит пар 14. А теперь мы выбрали другой первый, с ним тоже можно составить 14 пар. И так далее. Получается 14 + 14 + 14... и так

раз.

Отсюда и берется правило произведения: 15 · 14 способов.

Но есть одна хитрость. Я хочу посчитать пары независимо от по­рядка кружочков. Чтобы вот такие пары (см. рис. 13) не различа­лись. Что надо сделать с количеством способов?

 

Слушатель: Разделить на два.

А. С.: Да. Мы любую такую пару посчитали два раза. Один раз. когда мы сначала взяли синий круг, а потом белый. В другой раз мы первым взяли белый круг, а вторым синий. То есть мы каждую пару посчитали два раза. Поэтому ответ (15 · 14): 2 = 105.

Мы посчитали число имеющихся пар из 15 элементов «Цэ из 15 по 2». как говорят математики. «Цэ» означает первую букву слова combination (комбинация). См. формулу (1).

_С 2_ ₌  15_14 _{= 105>} ^

Математики любят символы. Но зачем они? Затем, что иначе придется очень много писать. Символы и язык математики нужны, чтобы сокращать запись. Почему древние греки и римляне не до­шли до современных высот математики? Потому, что они тратили очень много времени на лингвистическую работу перевода мате­матики в слова (и обратно: слов в математику). А вот когда ма­тематика перешла на символы, начался прорыв, о котором я еще расскажу.

Вернемся к нашим змейкам (формула (2))3. Первая из них со­ответствует измененной позиции, а вторая – исходной:

(1, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 14, 15, 13)

(1, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 15, 14, 13)

Для каждой пары чисел в каждой строке (а пар всего 105) мы спрашиваем, в правильном ли порядке написаны числа.

Слушатель: Частично да, частично нет.

А. С.: Верно. Например, 1 и 2 – в правильном порядке.

Слушатель: И последующая пара (2, 3) – тоже.

А. С.: Да, и следующая, и следующая за ней. То есть (4, 8).

Слушатель: В смысле «в правильном порядке»?

А. С.: «В правильном» не значит, что числа в паре соседние: и в (2, 3), и в (2, 7) – числа в паре расположены в правильном порядке.

Слушатель: По возрастанию.

А. С.: Да, по возрастанию. Большее следует за меньшим. Но, например, пара (15, 13) «нарушает порядок», потому что вначале идет большее число, потом меньшее.

Посчитаем количество пар, которые стоят в неправильном по­рядке. То есть по убыванию.

Слушатель: Простите, но ведь мы сами выбрали такую запись в виде извивающейся змеи. Мы разве не могли записать как‑ то иначе?

А. С.: Могли. Могли записать иначе, но тогда мы бы не преуспе­ли в доказательстве того факта, который нам нужен.

 

Математика дает полную свободу исследователю. Когда он провел рассуждение и сказал: «Теперь всё доказано», – он оправ­дывает всё, что построил. Математик скажет: «Рассмотрим то‑ то и то‑ то». Зачем? Ужас, зачем, это рассматривать? А по­том раз – и всё получилось (невзирая на «ужас»), Мат ем am и‑ ка – самый свободный род занятий. Никакой моды, нет, ничего.

 

Если вы, доказали недоказанную гипотезу, то чем бы вы ни пользо­вались, всё прощается. Победителей не судят (но иногда их слегка журят за сложноватое доказательство).

Итак, зачем я считаю пары, и почему так выписал змейку, пока не будет, понятно. Мы, договорились о некотором правиле. Мы, именно так выписываем числа. Вам придется принять это как есть. А дальше я считаю количество пар, которые стоят в неправильном порядке. Раз, два, три, четыре, пять, шесть... (см,, рис. 14).

 

Условно разобьем наш ряд из 15 чисел на 4 группы в соответ­ствии с номером строки. Рассмотрим для начала пару, элементы которой принадлежат разным группам. Ясно, что такая пара обя­зательно будет «правильной», так как любой элемент из группы слева меньше любого элемента из группы, стоящей правее: у нас группы от 1 до 4. от 5 до 8. от 9 до 12 и от 13 до 15. Значит, «непра­вильные» пары следует искать внутри групп. В первой и третьей группе всё хорошо, поэтому считать надо только оставшиеся две группы. Во второй группе 6 неправильных пар (8. 7; 8. 6; 8. 5; 7. 6; 7. 5; 6. 5). В четвертой группе чисел (для змейки, соответствующей измененной позиции) неправильных пар 2. Итого 8. А сколь­ко неправильных пар в исходной позиции? (См. нижнюю строку на рис. 15 или в формуле (2) выше. )

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: