Слушатель: Выпрямить.

А. С.: Да. Удалить вершину и выпрямить границу, убрав ненуж­ный «кусок границы». Что изменилось?

Слушатель: Минус вершина.

Слушатель: Минус ребро.

А. С.: Минус ребро, потому что из двух соседних ребер стало одно. Заметьте, что в выражении В – Р + Г опять ничего не изме­нилось. Итак, я буду упрощать картинку дальше (см. рис. 36).

Что происходит, когда я сниму еще ребро?

Пусть возникнет еще одна аномалия такого же типа. Возник­нет вершина, из которой торчит ребро, и на другом конце ребра висит пустая вершина. Но по‑ прежнему В – Р + Г такое же. как было раньше. Что я теперь могу сделать с этой вершиной и этим

ребром? Стереть их целиком. При этом количество и вершин, и ре­бер уменьшится на 1 (рис. 36). Значит, выражение опять не изме­нилось. а «сеть» на поверхности стала проще.

Я значительно увеличил грань, я убрал всё внутри нее. а вы­ражение не менялось. «Сеть» свелась к двум граням, охваты­вающим сферу «сверху и снизу», разделенным замкнутой лома­ной; в ней количество вершин равно количеству ребер, то есть В^Р + Г = Г = 2.

Для сферы формула Эйлера тем самым доказана.

Вопрос: «В какой ситуации логика этих рассуждений не мо­жет быть проведена? » Математик всегда изучает, в каком месте его рассуждение не пройдет. А не пройдет оно. например, на торе. На торе берем вершину и 2 ребра (рис. 37).

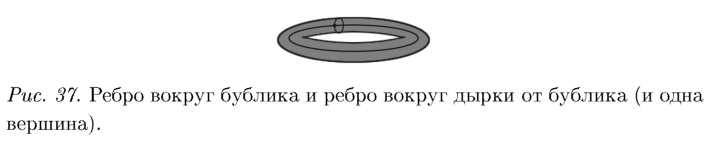
К такой картинке (рис. 37) приводится сниманием ребер любая «сеть» (достаточно общего вида ) на торе. Почему же нельзя снять еще одно ребро? Здесь я взываю к интуиции слушателей. Если мы разрежем тор по этим ребрам, а потом развернем, то получим квадрат. Чтобы лучше себе всё это представить, проделаем данные операции в обратном порядке: возьмем обычный квадрат из гибкой резины и изогнем его так. чтобы две противоположные стороны квадрата совпали (и затем склеим по совпавшим сторонам).

Получилась трубка (две оставшиеся стороны квадрата превра­тились при этом в два колечка). Изогнем трубку таким образом, чтобы эти колечки тоже совпали (и склеим их). Вот и получился из квадрата тор. По местам склеек восстанавливаем, где на этом торе расположены два ребра и одна вершина (из четырех вершин квадрата получилась ОДНА вершина на торе).

Осталось пояснить только один важный вопрос: так все‑ таки можно или нельзя при изучении топологии делать склейки, раз­рывы и надрезы? Выше говорилось, что при этом может изменить­ся топологический тип объекта. Значит, если мы хотим сохранить топологический тип объекта, этого делать нельзя. Но можно без­болезненно делать многое другое: растяжение, сжатие, перемеще­ние, поворот объекта, увеличение его в несколько раз. Эти опе­рации позволяют представить изучаемый объект в самом простом для понимания виде. Например, конус (заполненный внутри) мож­но превратить в шар.

Однако, если мы хотим изменить топологический тип, то мож­но (и даже нужно) делать разрезы и склейки. Эти операции так часто применяются в топологии, что даже носят специальное на­звание: «топологическая хирургия». Более того, практически лю­бой интересный для изучения объект можно склеить из весьма простых кусков. Скажем, торическую поверхность можно полу­чить склейкой нескольких треугольных кусков. А когда склейка будет закончена, места склеек будут определять некоторую «сеть» на торе. «Сеть», составленная из треугольников (естественно, кри­волинейных), называется «триангуляцией». Простейшая «сеть» на торе (рис. 37) не является триангуляцией, так как она полу­чена не из треугольников, а из квадратов... точнее, из одного‑ единственного квадрата. Но этой беде легко помочь: когда мы вы­ше делали операции в обратном порядке, надо было на исходном квадрате нарисовать диагональ (то есть вместо квадрата далее рассматриваются «два склеенных треугольника»). После двух вы­шеописанных склеек из этого квадрата получится триангуляция тора. Она состоит (хотя в это и трудно поверить) из двух граней, трех ребер и одной вершины (к которой подходят все шесть концов этих трех ребер! ).

Можно порекомендовать слушателям купить свежеиспеченный бублик с маком и. прежде чем его съесть, внимательно осмотреть и понять, как именно проходят но его поверхности ребра данной триангуляции. Но специалист‑ тополог может представить себе эту триангуляцию даже с закрытыми глазами!

Проверьте, возьмите любую ненужную велосипедную камеру, разрежьте и попытайтесь развернуть. Сохранится тот факт, что грань выглядит как квадрат или как круг, то есть она. как говорят математики. : топологически ·тривиальна. Она выглядит почти как обычная плоская фигура. А вот если мы снимем ребро (т. е. сотрем его с поверхности тора) и потом разрежем по оставшемуся ребру, у нас возникнет нетривиальная фигура в виде кольца. (Кстати, слово «тривиальный» восходит к слову «тривиум», обозначающе­му начальный уровень образования в средневековых университе­тах. )

Колечко на плоскости (рис. 38) не является топологически три­виальным. у него внутри дырка. Получается, что нам запрещено убирать это ребро, потому что мы изменим тривиальный объект на нетривиальный. Математика прошла долгий путь, прежде чем смогла понять, чем формально квадрат отличается от кольца.

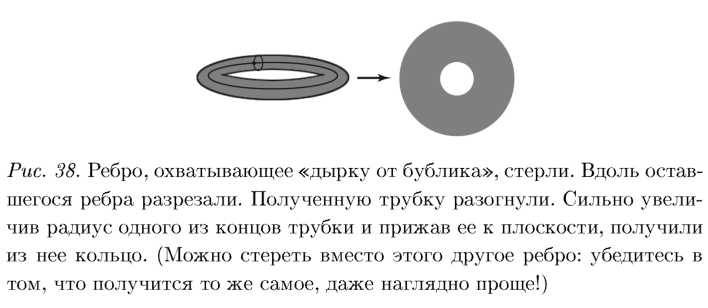
Но если мы примем к сведению этот путь, то сможем воспользо­ваться его результатами. Сможем сказать, что можно снимать ре­бро тогда и только тогда, когда объект, который возникает, будет топологически тривиален, то есть будет похож на квадрат но сво­ей топологической структуре. Именно поэтому я не имею нрава стирать на торе ребро.

Итак, чему равно В^Р+Г для нашей картинки (рис. 38)? Сколь­ко у нас вершин?