Слушатель: 9. Слушатели: Ничего. меняется. У нас оно пока равно 8. однако, если перемешать все фишки, согласно правилам игры «15». то количество неправиль­но стоящих нар изменится. Но удивительный факт состоит в том. что вы никогда

Слушатель: 9.

А. С.: Да. 9. Мы находимся на подступах к пониманию. Сейчас я покажу, что никакие изменения пустого места не меняют чет­ности, количества неправильных пар. Само количество, конечно.

 

меняется. У нас оно пока равно 8. однако, если перемешать все фишки, согласно правилам игры «15». то количество неправиль­но стоящих нар изменится. Но удивительный факт состоит в том. что вы никогда не измените четности, этого количества. Само ко­личество будет прыгать в сторону увеличения или уменьшения, но только на 2. на 4. на 6. словом, на ЧЕТНОЕ число единиц.

Начнем доказывать это утверждение. Где‑ то есть пустое место в коробке 4x4 (пусть конфигурация чисел, окружающих его. та­кая. как на рис. 16).

 

Пустое место может сдвинуться в 4 направлениях (рис. 17).

Давайте рассмотрим все 4 варианта и посмотрим, что произой­дет со змейкой.

Что происходит с выписанной змейкой чисел, если я передвигаю клетку с числом 11 налево?

 

Слушатели: Ничего.

А. С.: Правда. А что происходит со змейкой, если я передвигаю клеточку с числом 9 направо?

 

 

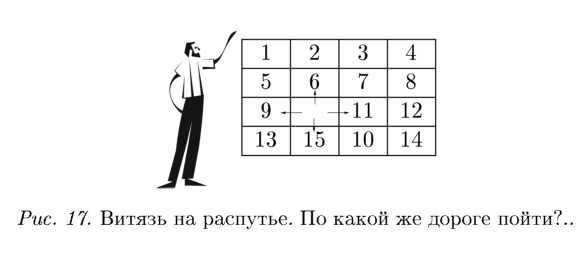
Слушатели: Ничего.

А. С.: Ответ верный. Два других варианта немного более слож­ные. но совершенно однотипные.

Что происходит, когда клетка движется сверху вниз или снизу вверх?

Слушатель: У нас появляются неправильные нары.

А. С.: Да. у нас либо появляются, либо пропадают неправиль­ные пары. Вопрос, сколько таких пар появляется и сколько про­падает? Ответ на этот вопрос зависит от того, где стояло пу­стое место. И вот здесь придется рассмотреть уже 4 варианта, но не для исходной стандартной змейки, а для любой. От самых простых в сторону самых сложных. Например, пусть в третьей строке получилось «9. 10. 11. пусто» (а номер 12 оказался в че­твертой строке за счет каких‑ то предыдущих перемещений) (см. рис. 18).

 

Записываю фрагмент змейки:

... 8, 7, 6, 5, 9, 10, 11, пусто...

Нас интересует только этот фрагмент, потому что при движении, которое будет совершено, слева и справа в змейке ничего не из­менится. Будет меняться только этот набор цифр. Расположение остальных пар не меняется. Внимание: «8» пошло вниз, пустыш­ка – наверх (рис. 19).

 

Как теперь будет выглядеть середина змейки? Вот так:

... пусто, 7, 6, 5, 9, 10, 11, 8...

Что произошло? Восьмерка из начала группы скакнула в ко­нец. Какие пары свое значение поменяли? Группа из шести чи­сел (7, 6, 5, 9, 10, 11) целиком сохранилась. Она просто поменялась местами с восьмеркой. Значит, какие пары поменяли, как говорят математики, «свой тип монотонности», то есть возрастание смени­лось убыванием (или, наоборот, убывание – возрастанием)?

 

Слушатель: (8, 7).

А. С.: (8, 7). Здесь теперь (7, 8); а еще?

 

Слушатель: (8, 6), (8, 5)...

А. С.: При том движении, которое я произвел, поменяют взаим­ное расположение чисел только те пары, в которых участвовало число 8. Поэтому 6 пар изменили тип монотонности. Если были возрастающими – стали убывающими, и наоборот.

Рассмотрим каждую пару в отдельности.

Было (8, 5) (числа в порядке убывания), стало (5, 8) – возраста­ние. Количество неправильных пар изменилось на единицу вниз.

Было (8, 10), стало (10, 8), количество неправильных пар измени­лось на единицу вверх. С остальными парами – то же самое. Ка­ждый раз мы добавляем или вычитаем единицу. Не может быть, чтобы где‑ то (вместо плюс/минус единицы) получился нуль, так как среди указанных шести чисел нет восьмерок (ведь каждое чи­сло, написанное на фишке, единственно).

Вне зависимости от знаков, количество изменивших тип моно­тонности пар всегда четно. Имеется 64 способа расставить знаки, но в результате всегда в качестве суммы получится четное число. Соседние плюс/минус единички либо добавят к сумме 2, либо до­бавят (–2), либо взаимно уничтожатся, давая ноль:

±1 ± 1 ± 1 ± 1 ± 1 ± 1

В каждой паре соседних плюс/минус единичек получится или 0, или 2 или –2. То есть общее изменение количества «неправильных пар» может произойти на 6, 4, 0, –2, –4, –6.

Изменения происходят на четную величину, поэтому исходное количество «беспорядков» (оно было равно 8) могло стать чи­слом 14, если все единички оказались бы с плюсом, могло остать­ся 8 (если бы было +1, +1, +1, –1, –1, –1). Могло стать 6, могло 4 или 2. Но никак не могло стать ни 5, ни 7.

В принципе, на этом месте я мог бы сказать «остальное проверь­те сами», потому что в других случаях передвижения пустой фиш­ки происходит ровно тот же самый эффект. Но давайте для акку­ратности проверим что‑ нибудь еще. Например, вверх могло пойти число 14 (вместо того, чтобы опустить вниз число 8) (см. рис. 20).

 

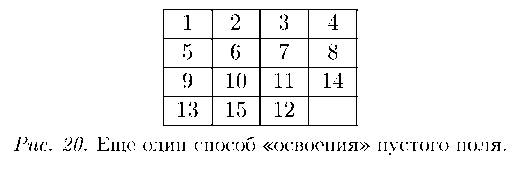
Что произойдет, где начались изменения? Только в нижних двух строках. Было 1, 2, 3, 4, 8, 7, 6, 5, а потом вместо 9, 10, 11, 14, 12, 15, 13 мы увидели 9, 10, 11, 14, 12, 15, 13. Ничего вообще не изменилось.

Давайте теперь представим себе внутреннюю пустую фишку. Скажем, если в позиции на рис. 18 клеточку 11 сдвинули к краю, а 7 сдвинули вниз (рис. 21):

 

Выпишем змейку до того, как подвинули 7:

1, 2, 3, 4, (8, 7, 6, 5, 9, 10, 11), 14, 12, 15, 13.

Теперь я двигаю 7 вниз и получаю вот такой фрагмент змейки:

1, 2, 3, 4, 8, 6, 5, 9, 10, 7, 11...

Выделяю в змейке группу, которая менялась.

Было: 1, 2, 3, 4, 8, (7, 6, 5, 9, 10), 11, 14, 12, 15, 13. Стало: 1, 2, 3, 4, 8, (6, 5, 9, 10, 7), 11, 14, 12, 15, 13.

6, 5, 9, 10 переехали на шаг левее, а 7 через них перепрыгнула. Сколько будет изменений? Ровно 4. Пары опять поменялись. Пра­вильные стали неправильными, и наоборот. Опять каждый раз мы прибавляем или отнимаем единицу. И так 4 раза. А 4 ведь – четное число, вот незадача. Опять результат меняется на четное число.

Что мы можем еще сделать? Мы могли вместо 7 подвинуть 12 (рис. 22). Тогда 12 прыгнет за пару (11, 14). Изменятся ровно две пары.

Слушатель: То есть нечетное число поменяться не может.

 

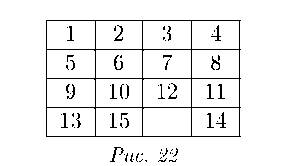
А. С.: Ни при каких условиях. Мы уже знаем, что движение по горизонтали – бессмысленно. Получится та же самая змей­ка. Если мы движемся сверху вниз, то количество неправильных пар меняется либо на 2, либо на 4, либо на 6, либо ничего не ме­няется. Можно честно перебрать все возможные переходы снизу вверх. Можно просто понять, что никаких других вариантов, кро­ме четных, нет. То есть в пятнашку выиграть нельзя, потому что в стандартной исходной позиции количество неправильных пар 8, и изменить его можно только на четное число. А в требуемой по­зиции имеется 9 неправильных пар.

Слушатель: Из любой ли позиции выиграть невозможно?

А. С.: Почему? На самом деле из половины всех исходных пози­ций. Из половины невозможно, из половины возможно. Потому что в «высокой» математике учат, что половина последовательностей имеет четное число неправильных пар, а половина – нечетное4. Поэтому половина вариантов будет собираться в стандартную ис­ходную позицию. Если пятнашки как угодно перемешать, вывалив из коробки и затем вставив обратно как придется, то перестанов­кой фишек всегда можно прийти либо к случаю «13, 14, 15», либо к случаю «13, 15, 14».

Чтобы понять, можно ли привести фишки в исходную позицию, нужно посчитать количество неправильных пар в змейке, соответ­ствующей изучаемой исходной позиции. Если оно нечетное – при­вести к исходной позиции можно. Если четное – то нельзя.

Слушатель: Какие числа можно поменять местами?

Другой слушатель: Например, 1 и 3 можно поменять?

А. С.: Если я меняю 1 и 3 местами (было 1, 2, 3, – стало 3, 2, 1), то как изменилась четность? Было отсутствие беспорядков (то есть 0), стало три беспорядка. Четность, стало быть, изменилась. Так что поменять в игре «пятнадцать» 1 и 3 местами, сохраняя остальные фишки на своих местах, тоже невозможно. Ваши вопро­сы относятся к теории групп, основе современной алгебры. Что и как можно поменять, чтобы четность менялась – этот вопрос напрямую к теории групп5. Почему ровно половина позиций име­ет четное количество беспорядков? Это тоже связано с некоторым фактом из теории групп. Сейчас я продолжу развивать эту тему. Рассмотрим «кубик Рубика». Венгерский инженер Рубик достойно продолжил дело, начатое Сэмом Лойдом.

Давайте разберем этот кубик и соберем его обратно.

Слушатель: По‑ моему, есть даже какие‑ то соревнования на этот счет.

А. С.: На соревнованиях надо собрать тот, который теоретиче­ски возможно собрать. Под словом «разобрать» я понимаю более радикальную операцию: «разодрать».

Как только мне купили кубик Рубика, я сразу его разодрал. Потому что мне было интересно, любую ли позицию можно при­вести к исходной. Мне было это настолько долго интересно, что на мехмате МГУ я решил соответствующую задачку в качестве зачета. Возможно (если мне не изменяет память) 12 разных рас­положений, не переводящихся друг в друга. В пятнашках – 2, а для кубика Рубика – 12 ситуаций. Это тоже следует из теории групп (по которой я и сдавал зачет).

Если перевернуть угловой кубик в кубике Рубика путем прину­дительного «раздирания» и восстановления его формы – его не­льзя будет собрать. Если перевернуть центральный кубичек в ре­бре – тоже нельзя. Если поменять местами два кубика малой «диагонали» любой грани – опять не получится. Эти изменения и все их сочетания задают набор различных позиций кубика Ру­бика, которые нельзя собрать. Однако это – трудная задача.

А теперь поговорим про мяч (рис. 3). То есть, как ни странно, снова про математику.

 

Математика состоит из двух важных составляющих: что такое число, и что такое доказательство. Моя старшая дочка не могла в свое время решить задачу: есть 3 апельсина и 2 яблока, сколько всего фруктов? Она совершенно не понимала, как можно сложить яблоки с апельсинами. Это же совершенно про разное. Мне кажется, что это типичное гуманитарное мышление. Че­ловек фокусируется на содержании объекта и не может от него уйти. А вот старший сын решал эту задачу, когда ему было два с половиной года. Я ему говорил: «У тебя было 3 грузовика и 2 лег­ковушки. .. » – «Ой, пап, давай просто 3 + 2, – зачем, всё это... ерунда... Говори три и два, и будем складывать». Ведь что такое число? Число – это ум, ен, и, е абстрагироваться от, объекта. Гово­рят, в каких‑ то таежных культурах, где‑ то далеко на воет, оке Сибири, имеются до сих пор разные числительные для обозначе­ния, например, количества белых медведей и количества деревьев. У них формализация числа 5 как выражающего общность пяти медведей и пяти сосен еще не произошла. На осознание того, что у 5 медведей и 5 сосен есть общее, человечество потратило мно­го тысячелетий. И в тот м, ом, ен, т,, когда это осознание настало, началась математика. А на память об этом процессе в русском языке до сих пор говорят «сорок» вместо «четырьдесят», хотя раньше можно было сказать «сорок собольих шкурок», но не «со­рок деревьев».

А теперь рассмотрим поближе футбольный мяч. Он состоит из шестиугольников и пятиугольников: двадцати шестиугольников и двенадцати пятиугольников.

Зачем? Почему так сложно? Вот вы, допустим, шьете футболь­ные мячи, чем вам не угодили просто шестиугольники? Взяли, сшили их по краям. Плоскость, например, отлично замощается ше­стиугольниками.

Слушатель: Но они, может быть, в мяч не сложатся.

А. С.: Давайте попробуем сложить огромный мяч. Возьмите 200. 300 шестиугольников. Плоек ость‑ то элементарно замощается? Вот так. как я нарисовал. Пчелиные соты (рис. 23).

 

Слушатель: Они на стыках но будут совпадать.

А. С.: Ну тут‑ то. на плоскости, вроде всё совпадает. А потом взял, свернул очень большой кусок плоскости и получил мяч.

Слушатель: Не остается места для того, чтобы правильно со­гнуть.

А. С.: Я даже не знаю, как выразить простым языком Ваше пра­вильное интуитивное замечание. Но математическая теория этого вопроса неумолима. Из шестиугольников нельзя собрать поверх­ность шара. Вообще, никак, никаким способом даже если их нарисовать на поверхности шара в слегка искривленном виде6

'edels/liexaspliere/. Обратите внимание па дату публикации: ‑ ))))·.

Слушатель: А из пятиугольников?

А. С.: Сейчас мы проясним ситуацию, связанную с пятиуголь­никами. Во‑ первых, давайте договоримся о том. что сшивать надо так. чтобы в каждой вершине сходилось три образующих поверх­ность мяча многоугольника. Будем называть такую сшивку регу­лярной. Сразу скажу, что никакой, регулярной ли. не регулярной.

никакой сшивкой из шестиугольников нельзя сшить футбольный мяч. Но давайте сейчас рассмотрим подробно регулярные сшивки. Возьмем всевозможные футбольные мячи, любого размера, кото­рые составлены из пятиугольников и шестиугольников.

 

Неожиданная теорема:

Если поверхность шара «сшита» регулярным образом из некото­рого количества х шестиугольников и некоторого количества у пя­тиугольников, то у обязательно равно 12.

Слушатель: В любом случае?

А. С.: В любом. Как ни экспериментируй, что ни делай, чему бы х ни равнялось, х = 200, х = 300, ... Но у = 12. Ровно 12, не 12 ООО, не 120. От размера мяча не зависит, от размера лоскутков не за­висит, от того, как сшивать, не зависит. Это – математическая теорема.

Слушатель: Невероятно...

А. С.: Есть абсолютное доказательство этой теоремы. Если вы хотите сшить футбольный мяч из пятиугольников и шестиуголь­ников, пятиугольников обязательно будет ровно 12.

Слушатель: Какой диаметр?

А. С.: Не важно: ни диаметр, ни размер лоскутков, ни то, как сшивать. Вы никогда не сошьете ничего другого. Какие бы прика­зы не издавала... ну, скажем, фабрика «Спортинвентарь». Ска­жем, придет к власти новая футбольная партия и скажет: «Отны­не сшивать мячи так, чтобы в них было поровну шестиугольников и пятиугольников». Тогда их обязательно будет 12 к 12.

Слушатель: То есть такое тоже может быть? Прямо 12 к 12?

А. С.: Да. А знаете, как еще может быть? Ноль шестиугольни­ков и 12 пятиугольников. Ни одного шестиугольника, одни пяти­угольники.

Слушатель: А зачем тогда шестиугольники?

А. С.: Видимо, для того, чтобы мяч был гладкий. Ноль шести­угольников – 12 пятиугольников. 200 шестиугольников – всё рав­но 12 пятиугольников.

Слушатель: Скажите, а вот эта теорема появилась уже после футбольного мяча? Или футбольный мяч появился раньше?

А. С.: Футбольный мяч появился «чуть‑ чуть» раньше. Если честно, теорему эту полностью осознали примерно 150 лет назад. Но этот результат, как и очень многие другие, должен быть отнесен к Эйлеру. Леонард Эйлер жил больше половины жизни в Петер­бурге и похоронен там же на Смоленском лютеранском кладбище. Он ввел в математику понятие инварианта. Эйлер показал, что есть в математике такие вещи, которые не меняются, что бы ты ни делал. И настоящая математика – это поиск таких вещей. Эйлер доказал потрясающую по красоте формулу, сейчас я ее нарисую, а может быть, даже докажу. Кстати, есть такой архитектурный объект «Монреальская Биосфера» или геодезический купол, со­зданный Ричардом Фуллером Бакминстером. Гигантский сегмент шара, чуть больше, чем полушар, составленный из маленьких ше­стиугольников. Я, когда его увидел, сказал: «Нет. Нет. Нет... Вы не правы, там не могут быть все шестиугольники, либо он сильно искривлен, либо там где‑ то живут пятиугольники. Ищите».

Мне говорят: «Алексей, как вы это угадали? Мы нашли 5‑ уголь­ники». Эта конструкция не полный шар, поэтому в ней не 12, а при­мерно 7 пятиугольников. Как же я узнал? Теорема, математика. Она же универсальная для всего. Что абсолютно одинаково в Рос­сии, в Канаде и в Америке? Только математика.

Слушатель: Положение этих пятиугольников, оно тоже опре­делено?

А. С.: Нет. Можно их все сцепить в одном месте. Только полу­чится сильно искривленная форма. Лучше пятиугольники разне­сти. Пятиугольники отвечают за искривление. А что такое искри­вление? Беру Земной шар и рисую на нём треугольник (рис. 24).

На Земном шаре есть где развернуться. Одну из вершин возь­мем на Северном полюсе, две другие – на экваторе. А сторонами треугольника, как и положено в геометрии, будем считать отрез­ки двух меридианов и отрезок экватора (ведь по ним измеряется кратчайшее расстояние между точками на земной поверхности! ).

 

Вот и получился у нас равнобедренный треугольник, у которого оба угла при основании прямые. А угол при Северном полюсе любой. Так давайте возьмем его тоже прямым!!!

У нарисованного нами треугольника все углы прямые. Такого не бывает на плоскости. Это геометрия шара, поверхности шара, и вот с этой геометрией связан рассматриваемый нами факт. Он открывает очень глубокую теорию дифференциальную геомет­рию, а также теорию римановых многообразий. Вернемся к фут­больному мячу, состоящему из х шестиугольников и у пятиуголь­ников, и к нашей «неожиданной теореме».

Слушатель: Кратен ли х чему‑ нибудь?

А. С «ж» может быть равен чему угодно. А вот «у» обязательно равен 12.

Слушатель: То есть четное, нечетное не важно.

А. С.: Абсолютно.

Слушатель: То есть мы можем сделать шар из 130 шестиуголь­ников и 12 пятиугольников, или из 131 и 12?

А. С.: Да, надо подумать и аккуратненько вклеить эти наши 12 пятиугольников.

Слушатель: А связано ли это с количеством сторон в пяти­угольнике и в шестиугольнике?

А. С.: Безусловно. Терпение, доказывать этот факт мы будем позже. Пока что нам нужна подготовительная работа, проделан­ная математиком Эйлером. Леонард Эйлер обнаружил следующий факт. Что такое многогранник. каждый понимает. Любой много­гранник это как бы изломанная поверхность шара. Эйлер нари­совал многогранник на шаре: спроецировал ребра и вершины мно­гогранника. лежащего внутри шара, на поверхность шара. (Слово «спроецировал» означает следующую процедуру: расположил вну­три стеклянного шара макет многогранника, сделанный из прово­лочек. и зажег в центре шара маленькую лампочку. На поверхно­сти шара будут видны тени от ребер это и есть проекции ребер. )

 

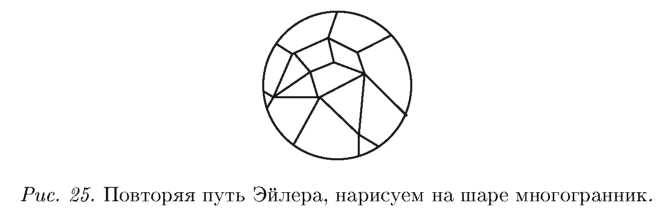
И с помощью этого приема доказал замечательную теорему с совершенно удивительной формулировкой. Называется теорема «Формула Эйлера для многогранника».

Пусть у многогранника будет: В количество вершин. Р количество ребер. Г количество граней. Эти количества мож­но непосредственно подсчитать, глядя на модель многогранника. Тогда обязательно будет

В^Р + Г = 2.

Независимо от того, какой мы взяли многогранник. Теорема верна и для куба, и для тетраэдра (рис. 26). и для любого другого мно­гогранника. имеющего границей «изломанную поверхность шара». Всегда это выражение будет равно 2.

Тетраэдр это любая треугольная пирамида. Раньше в такой форме делали молочные пакеты. Давайте посчитаем у молочного

 

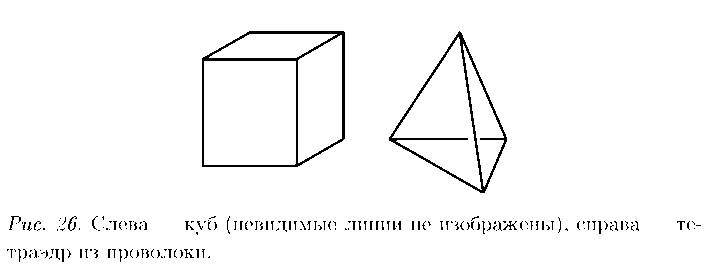
пакета количество вершин, ребер и граней. Сколько вершин у мо­лочного пакета?

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: