Слушатель: Нельзя.

А. С.: Иногда можно, иногда нельзя. Это – задача из теории узлов. Какие‑ то виды узлов можно распутать, какие‑ то нельзя. Сейчас я расскажу историю, которая может оказаться неправдой. Я слышал ее на лекции примерно 13 лет назад. Знаменитая про­блема узлов, топологических типов узлов, встала в первый раз на корабле пирата Дрейка в конце XVI века. Один из матросов это­го корабля тоже занимался узлами. Он завязывал много разных морских узлов и заметил, что некоторые из них – по сути один и тот же узел. Надо просто в одном месте потянуть, в другом прис­пустить шнур, и из первого узла получится второй (имеется в виду, что при этом концы узла должны оставаться связанными). Такие узлы называются «эквивалентными». И пирату в голову пришла идея классифицировать все виды узлов. Какие друг в друга пере­водятся без разрезания, а какие нет. Ему это не удалось, в чем, якобы, он честно признался.

Прошло 400 лет. И только совсем недавно был сделан большой прорыв в решении задачи об узлах. Сделали его отечественные ма­тематики Максим Концевич, Виктор Васильев и Михаил Гусаров.

Идея решения в том, что берут два узла, пишут для них неко­торые математические выражения, и если они разные, то и узлы тоже разные.

Вернемся к плоскости. «Простой» вопрос: какими много­угольниками можно замостить плоскость?

Что значит «замостить многоугольниками»? Я имею в виду сле­дующее. Вы заходите в магазин и выбираете себе паркет. Понра­вившийся вам паркет состоит из одинаковых дощечек такой формы (рис. 42):

Кто‑ то в страшном сне придумал такую форму. И таких до­щечек у вас немыслимое количество. Вопрос: «Можно ли собрать

 

из них паркет? Или они при сборке входят в противоречие сами с собой? »

Слушатель: Ну. скорее всего, центр еще получится, а вот по краям комнаты будут проблемы.

А. С.: Вы. наверное, уже видите, что не всякими плитками мож­но замостить плоскость.

Но доказать, что какой‑ то конкретной плиткой нельзя замо­стить довольно сложная задача. На самом деле, до сих пор не классифицированы даже все виды пятиугольников, которыми можно замостить плоскость. Найдено несколько пятиугольников, которыми можно замостить плоскость, но неизвестно, есть ли дру­гие. Открытая проблема10. Но тем не менее методами Леонарда Эйлера можно доказать следующую теорему.

Теорема. Не существует ни одного выпуклого 7‑ угольника, ко­торым можно замостить плоскость. Более того, восьми‑, девяти‑, десяти‑ и т. д. угольника тоже не существует.

А что такое «выпуклый»? Выпуклая фигура это такая фи­гура, у которой, если вы выбрали любые две ее точки, то весь отрезок между ними лежит внутри этой фигуры, не выходит за ее пределы.

 

Рис. J _t 3. Слова нсвыпуклая фигура, справа выпуклая.

Выпуклость одно из фундаментальных понятий математики. Такое простое определение, а на нём построена огромная сложней­шая теория с зубодробительными теоремами.

 

Почему же теорема требует выпуклости? Представьте себе цар­скую корону (рис. 44). Паркетина такой формы хотя и является 7‑ угольником, но он не выпуклый. Ниже мы увидим, что такими паркетинами МОЖНО замостить плоскость. Значит, если не тре­бовать выпуклости, доказать указанную выше теорему нельзя она просто неверна. Нельзя огульно утверждать, что паркетов из 7‑ уголышков не бывает. Не бывает только из выпуклых.

Рис. 44‑ Д° царской короны страшно даже пальцем дотронуться!

Сколько углов? Семь. Однако такой плиткой можно без проблем замостить плоскость.

Переворачиваем фигурку и вставляем корону в корону, а потом еще раз. два... (см. рис. 45).

Слушатель: А в конце как?

А. С.: До бесконечности. Мы же говорим о бесконечной плос­кости. Полосу сделать у нас получилось... (бесконечную в обе стороны). Ну. а если можно полосу, то мы ее размножаем неогра‑

 

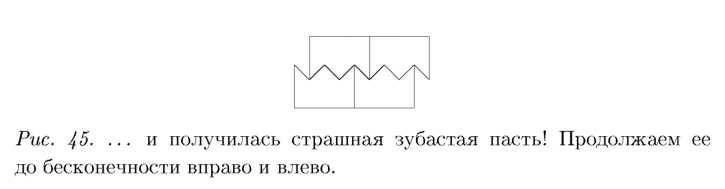
ниченно вниз и вверх, и всё. Мы «запаркетили» всю плоскость. А теперь я нарисую выпуклый семиугольник (рис. 46).

 

Априори совершенно не понятно, почему им нельзя замостить плоскость? Почему это так? Почему никакого семиугольника не­льзя предложить в качестве дощечки для паркета? Если Ваша невеста просит Вас: «Милый, я так хочу выпуклый семиуголь­ный паркет в нашу ванну! ». то это вариант «вежливого посы­ла» ибо такого быть не может. Сейчас мы докажем эту теорему. И в этом доказательстве у нас в первый раз возникнет бесконеч­ность «во весь рост». Как доказываются теоремы не существова­ния чего‑ то? Какой прием доказательства таких теорем?..

Слушатель: От противного?

А. С.: Точно. Предположим, что существует выпуклый семи­угольник. которым можно замостить плоскость. Не знаю какой, но какой‑ то есть. Предположим и приведем это предположение к противоречию. Итак, посмотрим на плоскость, которая замоще­на этими семиугольниками. Посмотрим на нее в «перевернутый бинокль» и увидим часть плоскости, как будто очень большую квартиру (см. рис. 47).

Я предупреждаю, такими доказательствами гоняют па ночь чертей. Приготовьтесь.

Начнем с того, что попробуем посчитать, сколько в квартире многоугольников. Давайте исходить из того, что наш семиугольник имеет длину 1 метр, а размер квартиры примерно 1 км.

 

На самом доле, но важно, какого что размера. Важно, чтобы вторая величина была неизмеримо больше, чем первая.

В данном случае «длина» семиугольника в 1000 раз меньше «длины» квартиры.

Слушатель: Что мы считаем длиной 7‑ угольника или кварти­ры?

А. С.: Например, самую большую диагональ. Это не очень важ­но. Тут математика немножко напоминает физику. Нужно несу­щественные детали не замечать, а на существенные обращать внимание. Когда у физика есть ниточка, она обычно имеет толщи­ну ноль. На самом деле у нее, конечно, есть толщина, но физикам она не важна. Вот и нам не важно. Возьмем какое‑ то измерение семиугольника (например, любую из его сторон или любую диаго­наль). Ведь все эти измерения НАМНОГО МЕНЬШЕ, чем «длина квартиры» что бы мы ни понимали под этой длиной. На полу квартиры в нормальной ситуации помещается очень много парке­тин. Форма пола квартиры тоже неважна, поэтому будем считать

его кругом радиуса R (где R может быть как угодно велико).

Не забывайте, что нам приказано замостить не пол в квартире, а всю бесконечную плоскость.

А теперь давайте посмотрим, сколько примерно семиугольников таится внутри вот этого огромного круга? С точностью до поряд­ка? Если у нас диаметр круга в тысячу раз больше, чем диаго­наль семиугольника, сколько семиугольников примерно поместит­ся в круг?

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: