Слушатель: Миллион?. Зададим теперь следующий вопрос. Сколько примерно семи­угольников «живет» в районе границы этого круга (то есть за­цепляет за границу круга)?

Слушатель: Миллион?

А. С.: Миллион, правильно. Правильный физический ответ. Миллион. Не важно, что это будет 700 ООО или 5 миллионов. В рай­оне миллиона. Порядок величины такой. Это примерно миллион.

Слушатель: Почему миллион?

А. С.: Потому что у многоугольника размером 1 метр пло­щадь сопоставима с 1 м² – может быть, чуть меньше, чуть боль­ше. У круга, у которого диаметр 1 километр, площадь порядка 1000000 м². Значит, в круг влезает примерно миллион семиуголь­ников.

Зададим теперь следующий вопрос. Сколько примерно семи­угольников «живет» в районе границы этого круга (то есть за­цепляет за границу круга)?

 

Слушатель: 6000.

А. С.: Да, похоже. 2жг = 6000. Порядок этого числа – не мил­лион, а тысяча. То есть внутрь входит в районе миллиона семи­угольников, а на границе их несколько тысяч. А теперь – вни­мание! Я стираю все многоугольники, которые не лежат в этом круге. Затем беру плоскость и, как грузинский хинкали, сжимаю ее в сферу (рис. 48).

Делаю я это, чтобы воспользоваться формулой Эйлера:

В^Р + Г = 2.

Грубо говоря, вместо круга есть поверхность огромного шара, у ко­торого верхняя шапочка (почти плоская) вся испещрена семи­угольниками. Но для картинки на всей большой сфере верна фор‑

 

мула Эйлера:

В ^ Р + Г = 2.

Давайте оцепим примерно, сколько у этой картинки будет вер­шин, ребер и граней? Одна огромная грань снизу, а наверху по­рядка миллиона граней в виде паркетин. Понятно, что одна грань погоды не делает. Более того, так как мы сейчас будем иметь де­ло с величинами порядка миллиона, то 2 в формуле Эйлера, или О тоже совершенно неважно. Я могу написать «примерно равно нулю». В – Р + Г примерно равно 0. Или В + Г и Р. Граней порядка миллиона. Г и 1000000.

Сколько вершин? 7000000 это вершин у всех многоугольни­ков; и в каждой из вершин сходится как минимум 3 многоугольни­ка. Может быть и больше (например, если у нашего 7‑ угольника есть острый угол в 30 градусов, и в вершине сошлись 12 этих острых углов), но не меньше это точно (ровно два угла не мо­гут со всех сторон окружить вершину, ибо каждый из них меньше 180 градусов). Поэтому вершин «не больше» (меньше или равно), чем 7000000/3. На самом деле я не учел вершины, которые явля­ются вершинами большой нижней грани. Сколько их примерно?

Слушатель: 6000.

А. С.: Да. Поэтому надо прибавить еще 6000. Нам не жалко!

7000000/3 + 6000.

Но шутка матанализа заключается в том, что 7000000 и 6000 не сопоставимы по величине, так как первая величина значительно

В 7000000/3.

Теперь о ребрах. Ребер будет 7000000/2. Причем делим в: точности на 2. без всяких меньше или равно, потому что каждое ребро мы посчитали ровно 2 раза:

Р = 7000000/2.

Слушатель: А почему мы каждое ребро посчитали ровно 2 ра­за?

 

А. С.: Потому что мы плиточку к плиточке прикладываем, без всяких зазоров (мы ведь предположили, что можно уложить без зазоров), см. рис. 49.

Рис. 49‑ Плиточка к плиточке! Ребро к ребру! Без зазоров!

Слушатель: Почему в теореме взято 7 сторон и более?

А. С.: Потому что шестиугольное замощение давно известно, на­пример. его знают наши друзья пчелы. Пятиугольное может быть таким: поставил домики рядом и сверху такие же. но вверх ногами (см. рис. 50). Домики, в отличие от царской короны, которую мы в самом начале рисовали, выпуклые.

 

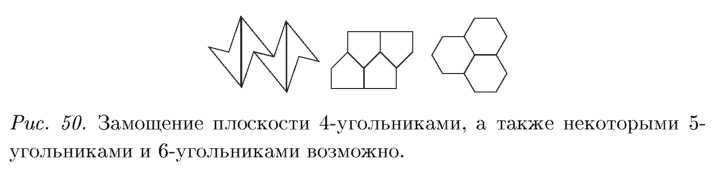
А уж квадратами, треугольниками замостить – это совсем лег­ко. Любым четырехугольником можно замостить плоскость и лю­бым треугольником – тоже. А вот какими пятиугольниками мож­но – это сложная задача. И про выпуклые шестиугольники тоже далеко не всё известно. Но какими‑ то можно. А вот выпуклыми семиугольниками уже никак нельзя.

 

Давайте все‑ таки доведем до конца доказательство.

У нас есть равенство

В + ГяР.

Оно говорит нам, что количество ребер должно быть того же са­мого порядка, что и количество вершин плюс количество граней. Подставим наши значения.

⁷⁰°0⁰⁰⁰ ^ 1000000 +7000000.

d

Если посчитать, сократив на миллион и умножив на 6, равен­ства не получается. Очень заметно не получается! Потому, что 21 не равно 20. Так что никакая добавка слагаемого типа 6000 дела не спасет, ибо эту добавку тоже придется делить на 1000000, и она станет исчезающе малой. А ведь мы могли взять не R = 1000 км, a R = 20000 км. Тогда бы процентное влияние добавки типа «6000» стало бы гораздо меньше. То же самое, естественно, будет

с восьми‑, девяти‑ и прочими «много‑ много‑ угольниками». А вот для шестиугольников как раз получается

6000000/2 = 6000000/3 + 1000000 3000000 = 2000000 + 1000000 (при любом значении R).

Точное равенство получается потому, что шестиугольное замоще­ние устроено так, что в каждой вершине сходится ровно 3 ребра. А вот уже 5‑ угольное замощение устроено иначе. Иногда 3 ребра сходится, а иногда – 4. У квадрата везде сходятся 4, а у правиль­ных треугольников – 6 ребер (рис. 51).

То есть выпуклое замощение бывает треугольное, четырех­угольное, пятиугольное, шестиугольное. А никаких других не бы­вает.

Слушатель: А какая практическая польза?

А. С.: Ну, наверное, есть какая‑ то. Математик никогда не ду­мает о практической пользе. Другие за него думают. Посмотрит какой‑ нибудь строитель: «О, значит не надо даже думать о том, чтобы использовать семиугольные плитки». А для математика нет такого вопроса. Это же совершенство. Это всё равно, что спраши­вать, какая практическая польза у молитвы. Так же и математик, он просто показывает: нельзя, – ура, вот какая интересная тео­рема. А польза? Наверняка какая‑ то польза есть. У любого кра­сивого факта есть польза.

Врезка 4. Ни один из слушателей не спросил у меня: «А где же в доказательстве теоремы используется тот факт, что исход­ный семиугольник был выпуклым? » И даже сложилось преврат­ное впечатление, что для проведения доказательства выпуклость 7‑ угольника вообще не нужна. Но она нужна! Ведь иначе получи­лось бы, что мы заодно доказали, что для невыпуклого семиуголь­ника тоже нельзя придумать замощение плоскости таким кусоч­ком. Выше, однако, приведен пример, что 7‑ угольным кусочком типа «царская корона» вполне можно замостить плоскость.

На самом деле выпуклость была незаметным образом исполь­зована, когда мы поделили число 7000000 именно на 3. Толь­ко для выпуклого 7‑ угольника можно опираться на число 3. На рис. 45 паркет содержит такие вершины, где сходятся только две плитки паркета (и на одной из них имеется угол БОЛЕЕ 180 градусов). Подобное явление, однако, возможно только для невы­пуклых плиток: любой выпуклый многоугольник содержит в себе только углы менее 180 градусов.

А. С.: Скажу напоследок вот что. Если кого‑ то не убедят тыся­чи и миллионы, надо будет сказать следующее. Если круг в п раз больше по размеру, чем плиточка, то количество граней, вершин и ребер имеет порядок п², потому что их количество связано с пло­щадью круга. А то, что в районе большой окружности «живет», имеет порядок п, потому что вопрос связан с длиной окружности. И если вы исследуете некоторое выражение порядка п², например,

Ti ² 7 /I² 9

– –г, –Ь п, и при этом во все слагаемые примешивается ме­лочь порядка п: 2п, 3п, 6п и так далее, то матанализ разрешает ее стереть, потому что п² и п «разного порядка роста». И неравенство будет верным при любом п, начиная с некоторого места. (А именно с того места, когда п² станет подавляюще большим по сравнению с п. )

В матанализе есть основной принцип: если вы про какое‑ то чи­сло показали, что оно меньше сколь угодно малого положитель­ного числа, то вы доказали, что оно равно нулю (если оно изна­чально не было отрицательным). Вот вы получили какое‑ то чи­сло, вы хотите доказать, что оно равно нулю. Покажу типичный

прием матанализа. Пусть есть число а. Рассмотрим такое число,

1 как –, и покажем, что наше число меньше, чем –. Допустим,

это мы доказали для любого натурального значения п. Для 1000, для 1000000, для 1000000000. .. Если вы умеете доказать такое не­равенство для любого п, значит, вы умеете доказать, что а равно нулю.

Вот в этом, собственно, весь принцип матанализа и заключен. Всё остальное, что есть в матанализе: интегралы, производные – не более чем упражнения с этой логикой (математики говорят в этом случае: «Применим технику работы с порядками бесконеч­но малых»),

И самый последний пример. Мне рассказал его папа, когда я еще даже в школу не ходил. Папа взял яблоко, отрезал от него половинку и говорит: «Это сколько от яблока? » – «1/2», – ска­зал я. – «А если теперь я к этой половинке прибавлю половинку оставшейся половинки, то это что здесь надо написать? »

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: