 |
б) Простий категоричний силогізм(дедуктивний умовивід, який складається із двох засновків і висновку, представлених судженнями виду: АSР,ЕSР, ІSР, OSР.)
|
|
|
|
б) Простий категоричний силогізм(дедуктивний умовивід, який складається із двох засновків і висновку, представлених судженнями виду: АSР, ЕSР, ІSР, OSР. )
Будь-який умовивід ( М ) породжує нове знання ( Р ). 2. Оскільки категоричний силогізм ( S ) належить до
класу умовиводів ( М ), то Отже, він ( S ) породжує нове знання ( Р ). за структурою складається із трьох термінів: S, М, Р.
Термін, що входить до висновку як його суб'єкт називається меншим і позначається буквою S. Термін, який виконує роль предиката висновку називається більшим і позначається буквою Р. Термін, що входить в обидва засновки, але відсутній у висновку, називається середнімі позначається буквою М.
Якщо розглядати структуру силогізму в залежності від розташування трьох термінів, то можливі чотири
схеми: 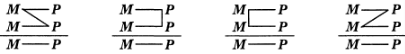
Ці схеми називають фігурами категоричного силогізму, тобто різновидами категоричного силогізму, які визначаються розташуванням середнього терміна.
Різновиди категоричного силогізму розрізняють за формами засновків і висновку. їх прийнято називати модусами категоричного силогізму.
При побудові категоричного силогізму дотримуються певних правил, які поділяються на:
а) загальні правила категоричного силогізму(ЗПС) 1. У простому категоричному силогізмі повинно бути лише три терміни. 2. Середній термін повинен бути розподіленим хоча б в одному з засновків. 3. Якщо крайній термін розподілений (або не розподілений) у засновку, то він повинен бути розподіленим (або не розподіленим) у висновку. 4. Якщо один із засновків заперечувальне судження, то і висновок буде заперечувальним судженням. 5. Якщо один із засновків часткове судження, то і висновок буде частковим судженням. 6. Із двох заперечувальних суджень висновок отримати не можливо. 7. Із двох часткових суджень висновок отримати неможливо.
|
|
|
б) спеціальні правила фігур. Перша фігура: 1. Більший засновок — судження загальне. 2. Менший засновок — судження стверджувальне. Друга фігура: 1. Більший засновок повинен бути загальним судженням. 2. Один із засновків заперечувальне судження. Третя фігура: 1. Менший засновок — стверджувальне судження. 2. Висновок — часткове судження. Четверта фігура: 1. Якщо більший засновок стверджувальне судження, то менший повинен бути загальним судженням. 2. Якщо один із засновків заперечувальне судження, то більший засновок повинен бути загальним судженням.
Використовуючи ЗПС і спеціальні правила фігур, для кожної фігури можна вивести усі правильні модуси. У межах кожної фігури можливі 16 комбінацій засновків від чотрирьох видів суджень АSР, ЕSР, ІSР, OSР: АА ЕА ІА ОА
АЕ ЕЕ ІЕ OЕ
АІ ЕІ II OI
АО ЕО IO OO
Перше правило виключає повністю комбінації 3 і 4 колонок. Варіанти 2 і 4 першої колонки суперечать першому правилу фігури. Варіанти 2 і 4 другої колонки виключаються з розгляду за 6 — ЗПС.
Отже, залишаються комбінації АА, АІ, ЕА, ЕІ із яких отримують модуси ААА, АII, ЕАЕ, ЕІО. Кожний модус має конкретне ім'я, що використовується як певний мнемонічний засіб: Barbara, Celarent, Darii, Ferio.
Логічна коректність модусів II, IIІ та IV фігур встановлюється за допомогою модусів першої фігури та відповідних правил висновку.
Для того, щоб встановити правильність силогізму необхідно здійснити такі кроки:
а) Знайти засновки і висновок даного силогізму. б) Визначити середній (М), більший (Р) та менший (S) терміни досліджуваного силогізму. в) Визначити більший та менший засновок. г) Перевірити дотримання загальних правил силогізму. д) Втановити фігуру досліджуваного силогізму. є) Перевірити чи відповідає даний силогізм правилам, тієі фігури за якою він побудований.
|
|
|
Силогізм, у якому пропущено один із засновків, або висновок називається скороченим силогізмом, або ентитемою.
Термін « ентимема » походить від грецького inthymos, що означає «в думці», «на думці» тощо.
Існує три види ентимеми: а ) Ентимема з пропущеним більшим засновком. «Земля має природний супутник, тому що вона планета»; б) Ентимема з пропущеним меншим засновком. «Земля має природний супутник, тому що усі планети мають природні супутники»; в) Ентимема з пропущеним висновком. «Всі планети мають природний супутник, а Земля — планета».
Для того щоб відновити силогізм у повному вигляді необхідно здійснити такі кроки: а) Визначити, що дано в ентимемі: два засновки, або один засновок і висновок; б) Знайти терміни силогізму в наявних частинах силогізму; в) Відновити по знайдених термінах силогізму відсутню частину силогізму; г) Застосувати алгоритм перевірки силогізму до реконструйованого силогізму.
|
|
|


