Квадрат, разделенный диагоналъю^2

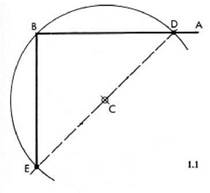
Рисунок 1. 1. Начертите любую линию АВ и отметьте какую-либо точку С ниже прямой АВ, где-то ближе к ее середине. Из точки С радиусом СВначертите дугу, размером по крайней мере с полуокружность, так чтобы прямая АВ пересеклась с этой дугой в точке D. СоединитеС и Dи продолжите эту линию до тех пор, пока она не пересечет дугу в точке Е. Начертите прямую ЕВ, перпендикулярную к АВ.

Рисунок 1. 2. Из центраВрадиусом ВА проведите дугу до ее пересечения с BE в точке G. Из центровСи А радиусом АВ начертите две дуги, пересекающиеся в точке F. Начертите квадрат ABGF.

дите дугу, длиной по крайней мере в полуокружность, для получения точек Н и J. Пользуясь тем же методом, который применялся при построениях на рисунке 1. 2, завершите квадрат AGHJ.

Сторона квадрата AGHJ(квадрат 2) точно равна диагонали квадрата ABGF(первого квадрата).

Площадь квадрата 2 точно в два раза больше площади первого квадрата. (Это интуитивно очевидно, поскольку больший квадрат содержит четыре одинаковых треугольника, тогда как первый квадрат содержит только два. )

Сторона квадратаназывается его основанием или корнем ( 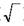). Сторона первичного

квадрата (квадрат 1) равна 1, а сторона квадрата 2 равна 2.

Диагональ квадрата 2 равна 2, ровно в два раза больше стороны первого квадрата.

Это отношение можно записать следующим образом:

Эти отношения кажутся логическим парадоксом, но если читатель изучит чертеж, он обнаружит, что они геометрически истинны. Даже тогда, когда квадраты увеличиваются в своих размерах, отношения их основания к диагонали остаются пропорциональными.

Рисунок 1. 4. Повторите операции, которые были проделаны на Рисунке 1. 3. Из центра Jначертите дугу, радиус которой равен стороне квадрата 2. Продлите стороны AJи Ш до тех пор, пока они не пересекут дугу в точкахКи М. Начертите квадрат 3, МКНА. Аналогичным образом постройте квадраты 4, 5, и т. д.

Отношение стороны к диагонали каждого квадрата и каждого квадрата к следующему, большему квадрату равно отношению квадрата 1 к квадрату 2. Это отношение можно записать следующим образом: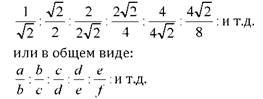

Такой тип прогрессии называется геометрической прогрессией, где числитель, будучи умноженным на знаменатель второго отношения, равняется произведению числителя второго отношения на знаменатель первого. Этот закон перекрестного умножения множества числителей и множества знаменателей остается истинным для любых отношений прогрессии, независимо от того, идут они один за другим или нет.

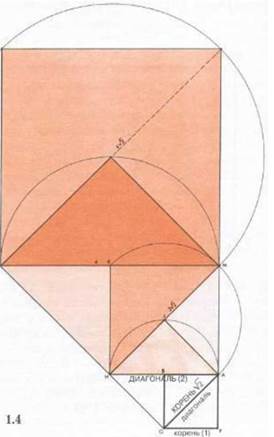
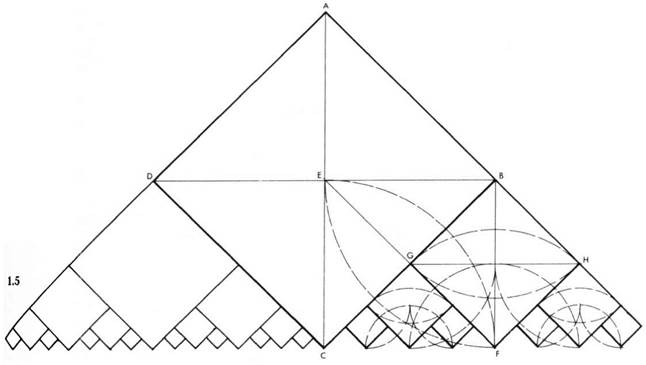
Рисунок 1. 5. Здесь представлен вариант предыдущей геометрической прогрессии, но продолженной в сторону убывания. В заданном квадрате АБСДначертите диагонали ББи АС. Из центров в точках# и С радиусом ЕВ, равным половине диагонали, начертите две дуги, пересекающихся в точке F. Начертите прямую EF, пересекающую сторону квадрата 1 в точке

G.

Из центров в точкахВи Fрадиусом GFначертите две дуги, пересекающихся в точке

G. Начертите квадрат BHFG(квадрат 2). Повторите этот процесс построения квадратов, которые постепенно уменьшаются в соответствии с геометрической прогрессией: 2, 4, 8, 16, 32 и т. д.

В обоих примерах квадрат и его диагональ отображают создание Двойки из Единичности (первоначальный квадрат) и последующий рост количества в геометрической прогрессии.

Квадрат, разделенный своей диагональю, дает архетипическую модель для геометрических пропорций и прогрессий такого типа: 1: V2:: ^2: 2, где каждый член (или отношение) умножается на постоянную величину, для того чтобы получить следующий член прогрессии. Постоянное пропорциональное увеличение или скорость может служить порождающей моделью для других бесконечно расширяющихся геометрических прогрессий, например: 1: V3:: V3: 3 или 1: 3:: 3: 9:: 9: 27. и т. д. (смотрите стр. 35). Данная геометрическая иллюстрация отношения между пропорцией и прогрессией вызывает в памяти алхимическую аксиому, говорящую о том, что все создаваемое формируется из неизменного, незыблемого компонента (пропорции), а также из изменяющегося, непостоянного компонента (прогрессии). Отношение между неизменным и изменяемым (между пропорцией и прогрессией) является ключом к Сакральной геометрии: все, что проявлено, будь это в физическом мире или в мире мысленных образов и концепций, принадлежит к вечно текущим прогрессиям постоянного изменения; и только непроявлен- ный мир Принципов остается неизменным. Наша наука ошибается, пытаясь пристегнуть неизменные, абсолютные законы и определения к изменяющемуся миру явлений. История науки демонстрирует нам постоянный отказ или пересмотр одной модели мира за другой. Из-за вызывающего беспокойство, нестабильного качества научного знания не только наши физики, но также и наши философы, художники и все общество стали релятивистами. Но неизменные порождающие принципы остаются, и наше временное отрицание их имеет место только потому, что мы ищем постоянства в эмпирическом мире вместо его действительного места обитания - метафизического.