Комментарии к Рабочей книге 2

Существует небольшое количество фигур, которые несут так много смысла, как простая ман- дорла. КейтКричлоу очень глубоко и деликатно исследовал эту форму в своей книге Время оста- новилосьи при объяснении геометрии Шартрского собора в его прекрасном фильме Отторжения,

так что я рассмотрю здесь только несколько символических интерпретаций этой формы.

Наложение кругов - прекрасное отображение клетки или какой-либо целостности в процессе ее преобразования в двоичность - образует рыбообразную центральную часть, которая является одним из источников символической ссылки на Христа как на «рыбу». Христос, будучи универсальной функцией, символически представляет эту область, которая соединяет вместе небеса и землю, низ и верх, создателя и созданное. Рыба также является символическим обозначением Эры рыб, и, следовательно, мандорла является доминирующей геометрической фигурой для этого периода космической и человеческой эволюции и является основным тематическим источником для космических храмов этого времени на Западе: в готических соборах.

Последовательность многогранников по мере их возникновения при дроблении единичности. По мере того как единичность, представленная крутом, начинает самоде- ление, ее центр становится двоичностью точекАи В Линия АВ естественным образом разворачивается в равносторонний треугольник (таким образом, все вещи, будучи двоичными по природе, являются троичными по принципу). По мере разворачивания равностороннего треугольника, он последовательно определяет стороны квадрата (4), пятиугольника (5), шестиугольника (6), восьмиугольника (8), десятиугольника (10) и двенадцатиугольника (12). Для построения этой фигуры начертите первоначальные круги, образующие мандорлу, затем начертите дополнительные крути, как это показано на рисунке. Различные точки пересечения по мере их возникновения будут определять вершины различных многоугольников (они показаны цветными линиями). Черные пунктирные линии указывают на другие точки соответствия и помогают определить другие вершины. Цветные линии указывают на местоположение пятиугольника поскольку это не является очевидным соединением точек (см. Рисунок 2. 6) Такой рост схож с ростом дерева. Мандорла может символизировать семя. Его прорастание приводит к появлению цветных окружностей (корень) и многоугольников (завязь, дающая начало ветвям). V3. содержащийся в мандорле, является формирующей способностью, дающей начало миру многоугольников.

Иисус, как центр мандорлы, несет идею о невещественном, вселенском «христовом» принципе, входящем в проявленный мир дуальности и формы. Эра рыб характеризуется формальной материализацией духа, проявляющейся в более глубоком проникновении духа в форму при параллельном углублении материализации духа: Слово становится плотью. Таким образом, квадратный корень из 3 связан с созидательным процессом, и эта связь проясняется далее при наблюдении за соотношениями между мандорлой и квадратным корнем из 3 в шестиугольнике, который представляет собой симметрию порядка для измерения земли, измерения времени (посредством

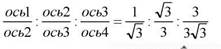
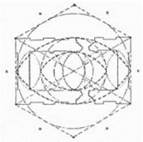
План часовни Святой Марии в Гластонбери основан на системе V3. Рисунок КейтаКричлоу из работы «Гластонбери, изучениемоделей» (Организация «Исследование утерянного знания», Лондон).

360° Великого круга небес), а также служит основой для образования кристаллов минералов, в особенности в структурах с углеродными связями, которые допускают образование всех органических веществ. При рассмотрении этого принципа образования с более строгой геометрической точки зрения мы обнаружим, что 72делит поверхность квадрата, а^Зделит объем куба, и мы должны вспомнить, что все в созданной вселенной является объемом. Образование любого объема структурно требует проведения триангуляции, следовательно, троичность является созидательным основанием для всех форм. Куб является наиболее элементарным символом проявленного (выраженного в объеме) мира форм.

Мандорла также проявляет себя как генератор форм в том, что все правильные многоугольники, можно сказать, возникают при последовательных построениях мандорлы.

Корни из 2 и 5 могут также быть получены из космограммымандорлы, поскольку нет такого синтетического символьного изображения Единичности, которое не заставило бы вспомнить все основные принципы (см. стр. 37): как говорится в Коране: «Нет бога, который не представляет собой всех богов». Но в мандорле^Зимеет особое значение благодаря богатому своеобразию перспектив, которые вызывает этот символ.

Отношение малых осей к большим осям мандорлы при постепенном росте обычно дает геометрическую прогрессию:

 

Рабочая книга 3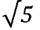

Рисунок 3. 1. Образование прямоугольника со стороной, равной 73, из прямоугольника с отношением сторон 1: 2. Начнем с удвоенного квадрата ABCD, который делится пополам по линии EF: из центра в точкеСрадиусом САпроведем дугу, которая пересекает продленную в обе стороны линию EFв точках Ни К. НК = V5- М! КЯпредставляет собой прямоугольник V5.

Рисунок 3. 2. ^Зи пятиугольник. Начертите круг, так чтобы его полуокружность была вписана в прямоугольник, образованный из двух квадратов, как это показано на рисунке. Продлите линию, которая разделяет прямоугольник на два квадрата так, чтобы завершить две главные оси XX и УУ круга. Из центраДрадиусом AY(= V5/2) проведите дугу до пересечения в точке В. Из центра У радиусом YBпроведите дугу до пересечения с окружностью в точках С и D. Из центров С и Д не меняя раствор циркуля, проведите еще две дуги, пересекающие окружность в точках Е и F. Начертите пятиугольник YDFEC.

Эти геометрические иллюстрации раскрывают взаимосвязь V5 и с числом 5 (являющимся квадратом V5), и с пятеричной симметрией пятиугольника.

3. 1.

 

вых) тел, которые служат основой для всех объемных форм. Также 2, 3 и 5 являются единственными числами, которые необходимы для деления октавы на музыкальные интервалы. Мы можем теперь рассматривать донные корни как троицу порождающих принципов.

Двойной квадрат, разделенный одной диагональю, образует два прямоугольных треугольника, каждый из которых имеет основание, равное 1, и высоту, равную 2. Для нахождения геометрического значения диагонали мы воспользуемся формулой Пифагора: a² + Ь² = с². В данном случае a = 1, b = 2, потому 1² + 2² = с² или 1 + 4 = 5, так что диагональ = У5, а полудиагональ в одном квадрате = V5/2.

Явление трех сакральных корней можно суммировать на этой простой диаграмме. Взаимоотношения, которые устанавливаются посредством этих трех корней, - это все, что необходимо для образования пяти правильных (Платоно

Комментарии к Рабочей книге 3

Кажется, что разделяющие и трансформирующие способности корня можно в то же время рассматривать как способности, которые связывают и синтезируют, поскольку эти принципы часто должны демонстрировать два полюса оппозиции. Квадратный корень из 5 пересекает два мира, обозначенных верхним и нижним квадратами, - мир духа и мир тела. И все формы связующих и промежуточных принципов между этими космическими пределами мы будем считать «христовым принципом». 75представляет собой пропорцию, которая открывает путь к семейству соотношений, называемых золотой пропорцией. Золотая пропорция порождает множество символов, которые использовались платониками в качестве обоснования идеала божественной или вселенской любви. Именно посредством золотого сечения мы можем осознать факт того, что Создатель посадил самовозрождающееся семя, которое поднимет смертное царство двоичности и неопределенности до уровня Бога.

Мы вкратце рассмотрим золотое сечение и его результаты. Но сначала давайте взглянем на принцип, который руководит прогрессиями, которые вытекают из сакральных корней из 2, 3 и 5.

Два основных элемента сакральной геометрии - крут и квадрат - в момент са- моразделения порождают три сакральных корня. Эти корни рассматриваются как порождающие силы или динамические принципы, посредством которых формы образуются и переходят в другие формы.

IV. ИЗМЕНЕНИЕ

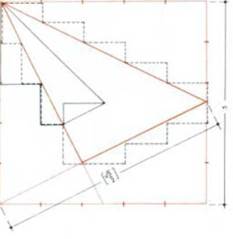
Получение сакрального треугольника со сторонами 3, 4, 5 путем пересечения трех по- лудиагоналей (V5/2) с демонстрацией геометрического доказательства этого. На рисунке также показаны отношения между процессом и структурой в Сакральной геометрии. Иррациональные корни, такие как V5, являются символами чистых архетипических процессов (порождение, слияние, трансформация и т. д. ), в то время как отношения, выраженные постоянными целыми числами, представляют собой структуры, которые возникают для отображения принципов этих процессов. На данном рисунке пересечение двух линий иррациональных процессов (V5/2) дает треугольник Пифагора со сторонами 3, 4, 5, фигуры, на которой основывается рациональность нашей математической мысли.

Мы подчеркивали зафиксированное, неизменное качество отношений несоизмеримых корней к Единичности по мере их возникновения в геометрических фигурах. Это аналогично стабилизирующей роли, которую функция корня играет в росте растения. Но корень также является генератором изменений в континууме вечно движущихся, необратимых фаз, которые являются частью органической жизни.

Поскольку древние мыслили как геометры, для них не существовало какого-либо разделения между геометрией и естественной наукой, или космологией, или теологией. Согласованность математики с естественными законами геометрии напрямую привела к одной из главных философских посылок древней мысли: изменению. В этой главе мы исследуем, как древние методы расчетов раскрывают этот универсальный закон и основываются на нем.

В древней математике не использовалась десятичная система, с помощью которой можно было бы показать, чему численно равен несоизмеримый квадратный корень из

2 (1, 4142135... ). Это было более чем ограничение, обусловленное системой обозначения; идея иррационального числа, такого как это, была для древнего геометра логическим абсурдом. Для него сутью числа было состояние: материальность, постоянство, измеримость. Ratio- латинское слово (корень которого присутствует в английском «reason», что означает разум, рассудок) также означает «измерение»; иррациональное число являлось неприемлемым противоречием.

Два типа чисел, рациональные и иррациональные, олицетворяли два полностью различных состояния. Целые числа относились к проявленному и представляли собой обозначения, которые использовались в вычислениях. Каждый аспект феноменального мира виделся как неизменный, мгновенный момент, обусловленный взаимодействием взаимодополняющих компонентов, момент, пойманный между светом и тьмою, жизнью и смертью, днем и ночью, между образованием, разрушением и изменением. Приостановленное образование олицетворялось в древней геометрии треугольником Диофанта, который представляет собой прямоугольный треугольник, все три стороны которого равны целым числам: треугольник со сторонами 3, 4, 5. Этот треугольник традиционно называется сакральным треугольником, «сакральный» означает неизменный или постоянный и, таким образом, символически относится к соединенным крестцовым костям позвоночника, которые позволяют принять неизменную позу в сидячем положении.

С другой стороны, иррациональные корни символизируют постоянство, созидательность действующей и противодействующей энергии. Эта огромная зреющая сила эманирует из непостижимой Единичности. А та, которую можно постичь, представляет собой не более чем кратковременную ограниченность этой Единицы, неопределимого Бытия в определенный момент «Так, необходимым образом все, что может быть определено, возникает из неопределимого всего».

Но глубокое почитание, которое формировало мысль древних математиков, не препятствовало использованию этих принципов в расчетах.

В нескольких математических текстах, предшествовавших Евклиду, дается метод, который позволяет выразить данные корневые отношения в виде последовательности отношений целых чисел. Эти отношения выстраиваются так, что приближаются поочередно то сверху, то снизу к значению несоизмеримого корня, т. е. в дополнение к этой изменяющейся структуре указанные последовательные отношения с каждым разом приближаются к значению корня все сильнее и сильнее.

Выраженные таким образом корни сохраняют свое динамическое качество, или качество «процесса», и в то же время выявляют Принцип Изменения.

Теон из Смирны, философ-платоник и математик второго века нашей эры, в своем труде «Изложение математических предметов, полезных при чтении Платона», привел числа, которые называются боковыми и диагональными. Я здесь приведу полное рассуждение Теона по этой проблеме, которое при первом чтении покажется не имеющей смысла головоломкой. Тем не менее, если следовать численной и геометрической процедуре, то путаница исчезнет, и вто же время метод расчета станет яснее, а вместе с этим и его философский смысл.

Теон начинает свою демонстрацию с квадрата, взятого в качестве единичного, в котором, по его заявлению, и сторона, и диагональ равны 1. Это описание свидетельствует об эзотерической значимости, поскольку квадрат со стороной и диагональю, равными 1, для нашего понимания является абсурдом. Но это в точности соответствует мистическому восприятию Единичности, которой обладали древние: для них все аспекты или различия - относятся ли они к стороне квадрата или к его диагонали - являются одним целым и равны единице, пока они находятся в рамках изначальной единичности. Когда дело дойдет до обсуждения спиралей, мы увидим, что другие численные прогрессии также непременно начинаются с такой двойной единицы, ее полезность станет очевидной, если на какой-то момент мы последуем за Теоном и воспользуемся его мыслью.

Ниже приводится демонстрация Теона, которая будет следовать этой же концепции с последующей геометрической интерпретацией:

«Подобно тому, как числа потенциально имеют отношения треугольные, четырёхугольные, пятиугольные и соответствующие прочим фигурам, так мы могли бы найти боковые и диагональные отношения, обнаруживающиеся у чисел в соответствии с порождающими отношениями, ибо по ним упорядочиваются фигуры. А так как над всеми фигурами согласно наивысшему порождающему отношению [т. е. отношению 1 к 2] начальствует единица, то и отношение диагонали к стороне отыскивается в единице. Возьмём, например, две единицы; положим, что одна из них есть диагональ, другая же - сторона, ибо единица, будучи началом всех вещей, потенциально должна быть и стороной, и диагональю. И пусть к стороне прибавляется диагональ, а к диагонали две стороны, ибо сколько дважды даёт в квадрате сторона, столько один раз диагональ. »

Это просто означает, что удвоенный квадрат стороны квадрата равен квадрату его диагонали. Он продолжает:

«Теперь большее становится диагональю, а меньшее - стороной: при первой стороне и диагонали квадрат единицы-диагонали на одну единицу меньше, чем дважды взятый квадрат единицы-стороны; ведь единицы находятся в равенстве, и единое на одну единицу меньше, чем двойное. Прибавим к стороне диагональ, то есть к единице единицу; итак, сторона будет иметь величину в две единицы; к диагонали же прибавим две стороны, то есть к единице две единицы; диагональ будет иметь величину в три единицы. Квадрат стороны будет 4, а квадрат диагонали будет 9; и 9 на единицу больше, чем удвоенный квадрат 2. Снова прибавляем к стороне 2 диагональ 3; сторона будет равна 5; а к диагонали 3 две стороны, то есть два раза по 2; диагональ будет равна 7. Квадрат стороны будет равен 25, а квадрат диагонали будет равен 49; и 49 на единицу меньше, чем двукратно взятое 25. Снова к стороне прибавь диагональ 7; получишь 12; к диагонали 7 прибавь дважды взятую сторону 5; будет 17. И квадрат 17, чей квадрат равен 289, на единицу полнее, чем двукратно взятый квадрат от 12 (288). И от дальнейшего прибавления, происходящего таким образом, будет происходить подобная же смена: двукратно взятый квадрат стороны то на единицу меньше, то на единицу больше, чем

*

квадрат диагонали; при этом стороны и диагонали рациональны».

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: