 |
Комментарии к Рабочей книге 5 5 страница
|
|
|
|
Symbols, Cambridge (Mass),
MIT Press, 1970, London, MITPress, 1977.
Michel, Paul Henri, De Pythagoreb Euclide: contribution cil'histoire des mathimatiques prkeuclidiennes, Paris, Belles Lettres, 1950. Michell, John, City of Revelation, London, Garnstone Press, 1972, New York, Ballantine, 1977.
Ntroman, D., Les Lqons de Platon, Paris, Niclaus, 1943.
Nicomachus of
Gerasa, Introduction to Arithmetic (tn. Martin Luther D'Ooge), New York, Macmillan. 1926; inEuclid, The Thirteen Books ofEuclid's Elements. Cambridge, Cambridge UniversityPress, 1926.
(NicomachusGerasenus), Manu el d'harmonigue et autrestextes rklatifs b la musique (trs. C. -E. Ruelle), Paris, Baur, 1881.
Pauling, Linus and Hayward, Roger, The Architecture ofMolecules, San Francisco, London, W. H.
Freeman, 1 %4.
Peet, Eric, TheRhind MathematicalPapyrus, Liverpool. LiverpoolUniversity Press, London, Hodder and Stoughton, 1923; Reston (Va. ), National Council of Teachers ofMathematics, 1979.
Plato, Timaeus (trs. ThomasTaylor), Minneapolis. Wizard'sBookshel f, 1975.
Puree, Jill, The Mystic
Spiral, London. Thames & Hudson, 1974, New York, Thames & Hudson, 1980.
Schwaller de Lubicz, R. A.. LeMiracle kgyptien, Paris, Flammarion, 1963.
---, Le Roi de
lathkocratiepharaonique, Paris, Flammarion, 1961(Forthcoming in English from InnerTraditions
International, NewYork. )
---, Symbol and the Symbolic, (trs. R. and D. Lawlor), Brookline(Mass. ), Autumn Press, 1978.
---, Le Temple de
l'homme. Paris, Caracteres. 1957, trs. R. and D. Lawloras The Temple in Man, Brookline(Mass. ), Autumn Press, 1977.
Schwenk, Theodore,
SensitiveChaos, London,
Rudolf SteinerPress, 1965,
New York, Schocken. 1978.
Smith, D. E., History
ofMathematics. 2 vols, New York, Dover, 1958.
Suares, Carlo, The Cipher ofGenesis (trs. from the French), London, Stuart & Watkins 1970, New York, Bantam Books, 1973.
Theon of Smyrna, The MathematicsUseful for Understanding Plato (trs. From the GreeklFrenchedn ofJ. Dupuis by R. and D. Lawlor), San Diego (Cal. ), Wizard'sBookshelf, 1979.
Thompson, D'Arcy, On Growth andForm, Cambridge UniversityPress, 1971.
Toben, Bob, Space, Time andBeyond, New York, Dutton, 1975.
Van den Broeck,
Andrt, Philosophical Geometry, SouthOtselic, New York, Sadhana Press, 1972.
Vitruvius, Ten Books
onArchitecture, New York, Dover, 1960.
Warusfel, Andrt, Les Nombres et leurs mystdres, Paris, Seuil, 1961.
Young, Arthur, The Geometry of Meaning, New York, Delacorte Press, 1976, London, Wildwood House, 1977.
\
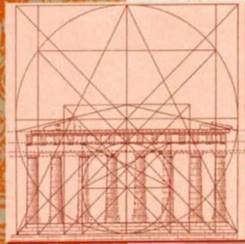
Фоберт Лолор предлагает нам методы анализа и расчетов форм и размеров самых разных объектов, как природных, таки созданных человеком Эти методы дают возможность понять гармонию цветка, готического собора, человеческого тела и музыки.
Мыслителям Древнего Египта, Греции и Индии было известно, что числа управляют практически всем, что есть в нашем мире, поэтому работа с ними позволяет приблизиться к Создателю.
|
|
|
С помощью простых наглядных примеров и упражнений он ведет читателя к глубокому пониманию логарифмически спирали, Золотого сечения, квадратуры круга. Освоив методы Роберта Лолора, можно понять идеи, которыми руководствовались великие архитекторы прошлого и которые сейчас применяются дли прогнозных моделей фондовых рынков, а пытливый ум найдет им и другое применение.

Цитируется по статье А. И. Щетникова Пифагорейский алгоритм для вычисления сторонних и диагональных чисел и понятие семенного логоса (http: //www. nsu. ru/classics/pythagoros/Algorythm_Teona. pdf).
Внимание следует обратить на две характеристики этих дробных прогрессий:
во-первых, чем дальше мы идем по последовательности, тем ближе отношение между числителем и знаменателем подходит к величине несоизмеримого корня из 5 = 2, 2360679...
Например, функция из нашей последовательности 29/13 = 2, 230. является приближением к значению V5, но немного меньше его. А следующая дробь 47/21 = 2, 23809. также является приближением к значению V5, но немного больше его. Идущая далее дробь 76/34 = 2, 235 опять меньше значения несоизмеримого корня, но гораздо ближе, чем предыдущее отношение; 123/53 = 2, 23636 больше точного значения, но все же ближе к нужному значению. Эта модель опять представляет собой колебание вверх и вниз, все сильнее приближающееся к надрациональному корню.
Второй характеристикой является то, что мы можем воспринимать эти последовательные числовые взаимоотношения как пространственные формы, т. е. квадраты и прямоугольники. Для преобразования этой последовательности в спиральную конфигурацию мы просто возьмем 1 в качестве стороны квадрата и добавим последовательность квадратов к уже существующей фигуре так, чтобы сторона каждого нового квадрата равнялась величине, на которую была увеличена предыдущая фигура, начиная с начальной:
|
|
|
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.
Первоначальный прямоугольник 1: 2 уже образован путем прибавления 1 к 1 (1 + 1), так что величина 2 становится длиной стороны квадрата, который добавляется к первоначальному прямоугольнику, давая в результате 3. Эта тройка становится стороной нового квадрата, который добавляется к предыдущему прямоугольнику 3: 2, образуя новое отношение 3: 5.
Отношение между двумя последующими членами этой последовательности стремится к ф. Логарифмическая функция ф(см. стр. 56) позволяет найти, взяв три последующих члена последовательности, например, ф2, поскольку выражение 1 + ф = фв точности соответствует выражению суммы 8 и 13 = 21, а отношение 13: 8 можно рассматривать как величину, стремящуюся к ф, тогда как 21: 8 является значением ф2.
Теперь возьмем нашу последовательность числителей и преобразуем их в пространственные фигуры, рассматривая отношение 1: 3 в качестве прямоугольника и прибавляя к ним квадрат так, как мы это делали раньше. Первый квадрат, сторона которого должна равняться 3 при прибавлении к первоначальным прямоугольникам, дает отношение 3: 4. Сторона второго квадрата будет равна 4, а четверка, прибавленная к 3, даст 7, что предоставляет нам второе отношение: 4:
7. Продолжая таким образом, мы получим последовательность чисел: 1, 3, 4, 7, 11, 18, 29, 76, 123, 199 и т. д.
www. e-puzzle. ru
www. e-puzzle. ru
|
|
|


