Комментарии к Рабочей книге 5 2 страница

Все эти спирали являются результатом процесса гномониче- ского роста, в котором квадрат и его гномон могут рассматриваться в качестве архетипической формы.

Эти диаграммы из книги Дарси Томпсона " О росте и форме" указывают на то, что спирали можно получить из треугольников и шестиугольников с помощью гномонического

роста.

Рабочая книга 6

Гномонические спирали

Приводимые ниже иллюстрации дают понимание древнего математического метода по образованию отношений целых чисел, которые довольно хорошо аппроксимируют несоизмеримые функции. Этот метод приписывается греческому математику Диофанту, но он, по всей вероятности, может являться частью более древнего математического знания. В приводимых ниже примерах мы можем обнаружить объединение гномонического роста, важных аддитивных прогрессий, прогрессии сакральных треугольников и количественных отношений, которые стремятся к сакральным корням из 2, 3 и 5. Все эти геометрические операции становятся основой для образования спиральных кривых, которые служат моделью для большого количества видов движения во Вселенной: от частицы до галактики.

Мы начнем с двух аддитивных прогрессий (мы уже встречались с ними при изучении числа ф, см. стр. 57). Мы посмотрим, как последовательности тех же самых чисел могут восприниматься также в качестве прогрессии развертывающихся (вращающихся) прямоугольников при образовании спирали. Наш метод будет заключаться в сравнении взаимоотношений между прогрессиями, вытекающих из двух важных отношений: 1: 2 и 1: 3. Для того чтобы сделать это, одна последовательность будет рассматриваться в качестве последовательности числителей, а вторая - в качестве последовательности знаменателей. Мы начнем с образования спирали на основании V5.

Выше приведена последовательность чисел, отличная от последовательности Фибоначчи, но опять отношение между последующими членами стремится кф, и каждый член образуется путем прибавления двух предыдущих членов.

Теперь мы можем объединить обе последовательности, в каждой из которых фвыступает в качестве отношения между каждым последующим членом, а отношение между членами этих последовательностей дает V5. Именно при таком объединении образуется спираль.

Используя этот метод, мы можем выработать план образования трех спиралей, которые будут соответствовать указанным законам геометрии и пропорции.

Рисунок 6. 1. Спираль корня из 5, начинающаяся с отношений 1: 2 и 1: 3.

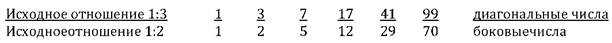
Для построения спирали V2 мы опять начнем с двух порождающих отношений: 1: 2 и 1: 3 для инициации прогрессий, которые будут образовывать последовательности из числителей и знаменателей:

Здесь мы видим два отклонения от формы V5, описанной выше. В этом примере ни однаиз прогрессий не начинается с повторяющегося числа 1, и здесь вместо простой аддитивной последовательности мы имеем каждый раз сложение сторон двух квадратов.

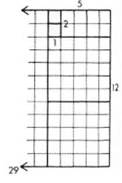
Рост осуществляется путем сложения двух равных квадратов, которые в качестве стороны используют большую сторону предыдущего прямоугольника. Так, к первоначальному прямоугольнику 1: 2 добавьте два квадрата со сторонами, равными 2, так чтобы получить сторону, равную 1+2 + 2 = 5; затем к прямоугольнику 2: 5 прибавьте квадраты со сторонами, равными 5, что даст 2 + 5 + 5 = 12, и т. д.

К первоначальному прямоугольнику 1: 3 мы прибавляем два квадрата со стороной, равной 3, что даст 1 +

3 + 3 = 7, ик этой 7 мы прибавим два квадрата со стороной, равной 7, получим 3 + 7 + 7 = 17 и т. д.

Последовательность 1, 2, 5, 12, 29. и т. д. представляет стороны квадратов, в которых диагонали соответственно равны 1, 3, 7, 17, 41. и т. д.

Соотношение между этими двумя последовательностями, отходящими от единичности («Единичность, - как говорил Теон, - в действительности является стороной и диагональю»), все сильнее и сильнее приближается к V2.

Рисунок 6. 2. Спираль V2, начинающаяся с соотношений 1: 2 и 1: 3, но с последующим прибавлениемдвух квадратов.

Внеся только несколько изменений в процедуру порождения, мы можем теперь построить прогрессию и спираль, относящиеся к V3. Изменения в данном случае заключаются в том, что отношение 1: 3 начинает последовательность 1, 1, 3. (а не 1, 3. ) и дает знаменатели вместо числителей, как это было в других двух спиралях. Для получения спирали V5 мы последовательно прибавляли один квадрат, для получения спирали 72мы последовательно прибавляли два квадрата, но в данном случае мы прибавим первые два квадрата вместо одного.

Начиная с исходного отношения 1: 2, мы прибавляем два квадрата со стороной, равной 2, и получаем 1 +2 + 2 = 5, затем один квадрат со стороной, равной 5, получая 2 + 5 = 7, и т. д., соблюдая в дальнейшем последовательность прибавления сначала двух, а затем одного квадрата.

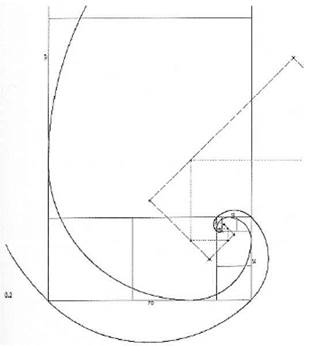
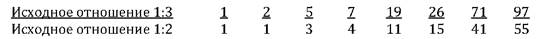
Исходная фигура 1: 3 строится в точности таким же образом и дает последовательность чисел, указанную выше.

Как и в случае с первыми двумя корнями, именно наложение числителей и знаменателей дает отношения, дающие V3. Благодаря «синкопируемому» прибавлению сначала двух, а затем одного квадрата, нельзя при таком построении нарисовать сразу две - внутреннюю и внешнюю

- спирали. V3, будучи созидательным принципом, выступает только как содержащая или внешняя спираль.

Рисунок 6. 3. Примеры построения спиралей, приведенные на данном рисунке, частично взяты из книги Р. А. Шваллера де Любича«Храм человеческий».

Более глубокая цель такого спирального развития числа вокруг надрациональных корней заключается в том, что нам предоставляется модель, в соответствии с которой неопределимая причина (корень) выражает себя посредством

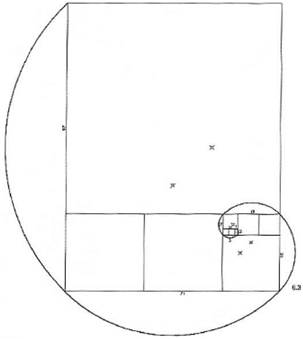
игры определяемых чисел и форм.

Спираль все еще остается нашим наиболее содержательным образом в отношении движения Времени, и поэтому она является главным элементом для нашего восприятия развития. Приводимый ниже отрывок из книги Шри Ауробин- до«Проблема возрождения» точно озвучивает то, что мы только что испытали при отображении вселенского закона языком геометрии:

«То, что окружает нас, представляет собой постоянный процесс в его универсальном аспекте, прошедшие моменты времени присутствуют в нем, содержатся в нем, исполненные и пройденные, но в общем и в своих подробностях они все еще повторяются в виде основания и подоплеки; настоящие моменты времени присутствуют в нем не в виде повторения в худшем свете, но в виде активного, оплодотворенного созревания всего того, что духу еще предстоит проявить: без иррационального повторения десятичных знаков, которые беспомощно возникают в цифрах бесконечным образом, но в виде развертывания последовательности божественных сил Бесконечного. Именно присутствующая в вещах Воля, великая и осмотрительная, неторопливая, неутомимая, движется через любые циклы ко все большему и большему раскрытию своего собственного облика в своей собственной бесконечной реально- сти. »(Курсив мой).

Комментарии к Рабочей книге 6

Логарифмическая спираль настолько богата геометрическими и алгебраическими гармоническими сочетаниями, что традиционные геометры назвали ее Spiramirabilis, что означает «чудесная спираль». В то время как радиус спирали возрастает в геометрической прогрессии, угол поворота радиуса возрастает в арифметической прогрессии. Эти две числовые последовательности дают все соотношения, из которых образуются музыкальные интервалы.

Таким образом, мы можем обнаружить в этих спиральных гномонических фигурах близкую связь между временными законами звука и пропорциональными законами пространства.

Представляется, что человеческий мозг эволюционировал посредством гномоническо- го расширения. То же самое луковичное тело (внутренняя или задняя часть мозга), которое играло главную роль в процессе рептильного периода эволюции, все еще присутствует внутри нас. Над ним размещается средний мозг -лимбическая область, которая была главным ментальным аппаратом в процессе эволюции млекопитающих; и, наконец, приходит время коры головного мозга у высшего человека.

Квадрат ку = 16

Я * Л S » ч

Квадрат ку = 16

Вписанный квадрат изображает квадрат коу = 9

квадрат коу = 9

Гномоническое расширение в природе позволяет увидеть элементы последовательного роста. Это интересным образом связано с нашим представлением о времени. Обычно мы воспринимаем время либо как скоротечное направленное движение от растворившегося прошлого через неуловимое настоящее к воображаемому будущему, либо, с мистической точки зрения, как всесодержащую вечную полноту. Гномонический принцип дает третье описание времени. Время здесь представляется в виде расширяющегося роста, эволюции, как можно выразиться, принадлежащей к энергиям сознания, которые вышли за пределы своих преходящих форм и сущностей. Как говорит китайская мудрость: «Все тело духовного сознания прогрессирует без остановки, а все тело материальной сущности без остановки разрушается». В такой модели прошедшее время остается в настоящем в виде формы, а структура растет посредством пульсирующего ритмического гномонического расширения. Удаление слоя или камеры, которые образовались совсем недавно, у раковины наутилуса в действительности представляет собой возвращение назад по его линии жизни. Формы, развивающиеся по логарифмическому закону, всегда несут в себе этот элемент памяти о прошлом и поэтому символизируют эволюцию не вещества, но сознания.

Древние китайские математические задачи, относящиеся к гномоническому принципу.

В гномоническом времени все его этапы присутствуют в постоянных слоях подобно структуре светового года галактического пространства, которое при каждом взгляде на усыпанное звездами ночное небо возвращает нас в прошлое далеких тел, а слои света за видимым светом представляют собой будущие энергетические волны, которые придут и окажут влияние на землю. Все аспекты материального мира, включая наши собственные тела, относятся, поэтому, к прошедшему времени, существуя в остаточном гномоническом слое, который уже пройден втекающими космическими энергиями. Эта идея выглядит немного необычно, хотя и не отличается от понятия времени, присущего нашим предкам. АтарваВеда говорит:

«Имя и Форма есть то, что осталось в Остатке. Мир есть то, что осталось в Остатке. Ин- дра и Агни есть то, что осталось в Остатке. Вселенная есть то, что осталось в Остатке. Небо и Земля, все Сущее есть то, что осталось в Остатке. Вода, океан, луна и ветер есть то, что осталось в Остатке».

В египетской иконографии квадрат и его гномон можно обнаружить в троне Осириса, на котором восседал фараон. Восседающий на троне фараон, как воплощение вечной солнечной энергии на земле, таким образом, ассоциировался с неподвижным элементом - квадратом и его гномоном, - который остается постоянным по мере роста и изменения. Однако этот трон также остается троном Осириса - божества, олицетворяющего цикличность изменений в природе, - в его потустороннем царстве потенциальных возможностей. В этом смысле трон представляет собой неизменную опору, на которой должны покоиться циклы постоянного движения Осириса.

Трон, на котором восседает Осирис, изображен в виде корня из 4 по мере его трансформации в корень из 5 с помощью принципа V5, на котором основываются все пропорции ср. Именно поэтому трон показан как место мира трансформаций, осуществляемых через смерть и возрождение, что и олицетворяет собой Осирис.

Эта фигура также олицетворяет переход от 4 к 5, то есть от царства элементов или минералов, которое ассоциируется с числом 4, к царству жизни, которое ассоциируется с числом 5, поскольку Природа начинает создавать пятиугольные фигуры только при появлении жизни. Первоначальная единичность, содержащаяся в четырех квадратах (22), выходит за свои пределы и образует гномон, пятую часть, которая равна площади каждого из других четырех квадратов.

Живущий фараон является не только представителем на земле вечной солнечной силы, он также является Хорусом, сыном Осириса, который получает и вновь приносит в мир силу своего отца. Отношение «отец-сын» или «живой фараон - мертвый фараон» особенно выделялось в традиционном обществе и может рассматриваться как пульсация гномонического удержания прошлого в настоящем и будущем. Если могущество и влияние умершего фараона, отца, относится к первоначальному квадрату, а энергии и деятельность живущего фараона относятся к гномониче- скому расширению, то у нас возникает образ социального порядка, основанного на отношении индивидуума к унаследованному им государству. Удивительная целостность древней египетской культуры на протяжении свыше трех тысячелетий демонстрирует непрерывное обновление, в котором, кажется, ничто не утрачено из основополагающего опыта прошлого.

Квадрат и его гномон служат архетипическим образом для некоторых видов роста в природе, а также в качестве образа времени и эволюции. Эта фигура обладает той ценностью, что может помочь заглянуть за пределы поверхности вещей, для того чтобы обнаружить лежащую в основе структуру, функцию ф своей собственной динамикой и механизмом.

При философском подходе к геометрии мы пытаемся воспринять характеристики формы, которые несут в себе смысл. Телеологическое послание присутствует, например, в самой спирали, поскольку она последовательно двигается в противоположных направлениях к окончательному проявлению бесконечно развернувшегося и бесконечно сжавшегося. Спираль постоянно сходится к этим двум непостижимым аспектам конечной реальности и поэтому символизирует вселенную, движущуюся к совершенной единственности, из которой она возникла. Таким образом, спиралевидные вихри нашей галактики создают образ непрерывности между фундаментальными полярностями - конечным и бесконечным, макрокосмом и микрокосмом.

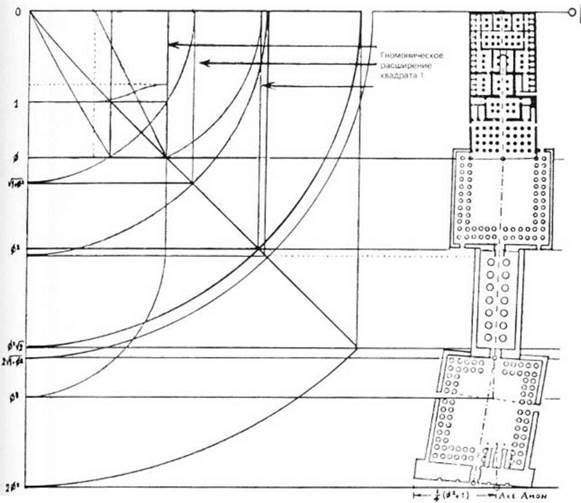
В архитектуре египетского храма в Луксоре, как и в индуистском храме, используется принцип гномонического роста, однако, используется он совсем другим образом. В данном случае этапы строительства храма, которые основываются на различных пропорциях ^первоначального квадрата внутреннего алтаря, совпадают с этапами роста человеческого гаи, которое символизирует весь план храма.

VI. КВАДРАТУРА КРУГА

В литературе по сакральной геометрии приводится ряд примеров, и все они относятся к одной идее, известной под наименованием «квадратура круга». Она представляет собой упражнение, в котором с помощью только обычного циркуля и линейки нужно найти способ построения квадрата, периметр которого должен быть равен длине окружности заданного круга или площадь которого должна быть равна площади заданного круга. Поскольку круг является несоизмеримой фигурой, основанной на п, можно нарисовать квадрат, только приближенно равный ему. Тем не менее, квадратура круга имеет большое значение для геометра-космолога, поскольку для него круг представляет собой чистое, не-проявленное дух-пространство, а квадрат является проявлением воспринимаемого мира. Когда между кругом и квадратом можно установить хотя бы приблизительное равенство, бесконечность может отобразить свои размеры или качества посредством конечного.

Рабочая книга 7

Квадратура круга

На последующих страницах мы понаблюдаем за квадратурой круга, которая, как я знаю, содержит немало символических ключей для постижения сотворения вселенной. Мы начнем с построения окружности, помня при этом, что она является геометрической метафорой однородного недифференцированного пространства. Как и на других наших диаграммах, это единство- пространство должно быть разделено на два с целью осуществления сотворения. Итак, начнем с разделения нашего единства-пространства на две части, с разделения, которое происходит внутри изначальной единичности.

Рисунок 7. 1. Начертите круг с центром в точкеО и радиусом ОА= 1. Начертите диаметры АА' и ВВ', так чтобы они пересекались под прямым углом. Из центров, расположенных на диаметре ВВ', начертите две окружности, радиус каждой из которых равен половине радиуса исходной окружности. Из точкиАпроведите дугу NM, которая должна касаться окружностей двух внутренних кругов. Проделайте то же самое из точкиА' Постройте квадрат АСВ'Она радиусе ОАисходного круга.

Дуга, радиус которой равен по- лудиагонали этого квадрата, указывает на то, что радиус АЕ дуги NEMравен ф, а дуги NEMи NDMделят радиусы АО иА'О в соответствии с Золотой пропорцией в отношении 1/фи 1/ ф².

При таком делении единого круга на два, которое служит основой для традиционного символа ян-инь, возникает интересный парадокс. Две длины окружности внутренних кругов вместе равны длине окружности большого круга, но площадь этих двух кругов составляет только половину площади изначального круга. Единица стала Двойкой. И индусская мифология, и средневековая европейская алхимия дают нам ту же метафору для постижения таинства того, как однородная единичность становится поляризованной дуальностью: когда однородное или тщательно перемешанное молоко оставляют на воздухе при средней температуре, в нем начинается кислотное брожение, которое свертывает молоко в сгущенные, жирные шарики, которые плавают в водянистой сыворотке. Таким образом, мы имеем разделение взаимно отталкивающихся форм, которые возникают из общего источника. Мифологически этот естественный процесс представлен в истории Каина и Авеля, Сета и Хоруса, Индры и Асуров, и т. д., во вселенском антагонистическом взаимодействии противоположностей, что и разует жизнь: это и есть инь и ян.

Когда мы геометрически формируем вместилище для двух кругов, рисуя дуги из каждого конца вертикального диаметра, так чтобы они касались двух кругов и так чтобы верхняя и нижняя дуги заканчивались на горизонтальном диаметре, мы видим, что эти две дуги делят вертикальный радиус ОА(который считается равным 1 или представляет собой единичность) в Золотой пропорции как 1/фи 1/ ф². Золотое сечение, будучи наиболее важным делением Единичности, здесь выступает аналогом невидимого «провокатора»: вселенской сжимающей или свертывающей силы. Также очевидно, что радиус этой окружности равен 1 + 1/ф, что равно ф.

Пузыреобразную форму, охватывающую первичную дуальность (аналогично мандорле из Рабочей книги 2, но в других пропорциях), можно найти везде в Египте в качестве символа Ра, солнечной, дающей жизнь силы, испускаемого Слова, рта, который называет имена богов, составляющих единицу. Рот Ра также напоминает форму вибрирующей струны (см. стр. 22).

Рисунок 7. 2. Дуга Ра, которая проходит по касательной к двум внутренним окружностям, пересекает внешний круг единичности точно в той точке, в которой начинается сторона правильного пятиугольника, вписанного во внешний круг: это точка J, если смотреть влево от верхней точки вертикального диаметра, и точка F, если смотреть вправо от той же верхней точки вертикального диаметра. Кроме того, поместив циркуль в нижнюю точку вертикального диаметра и нарисовав дугу, касающуюся нижних частей двух внутренних окружностей, мы можем получить точное местоположение третьей стороны того же вписанного пятиугольника, оканчивающегося в точке Нсле- ва и в точке Ссправа, там где указанная дуга пересекает внешний круг.

Затем, просто соединив две верхних стороны пятиугольника с каждым концом стороны, лежащей в его основании, мы получим правильный, вписанный в окружность пятиугольник.

Таким образом, первоначальное сжатие или разделение на две части лежит в основе получения конечного результата: пятиугольника, символа жизни, с его пятеричной симметрией, которая обнаруживается только в живых организмах. Он представляет собой фигуру, приписываемую физическому и витальному аспектам человека, который посредством пяти чувств воспринимает мир природы и, таким образом, побуждает его к существованию. Звезда пятиугольника, образованная диагоналями, проведенными внутри его, символизирует преобразованное или усовершенствованное человечество, поскольку все отрезки прямых этой звезды получаются в соответствии с Золотой пропорцией (см. стр. 52).

Рисунок 7. 3. Впишите исходный круг в квадрат. Затем начертите окружность, в качестве центра которой следует использовать центр исходного круга, а за радиус следует взять расстояние до вершины мандорлы. Длина окружности полученного круга будет равна периметру квадрата, который касается исходной окружности.

Первоначальное разделение, которое одновременно дает пропорции пятеричной симметрии, несет с собой телеологическое послание о Жизни как о силе непостоянства и возвращения к свету, мы видим это в растениях, которые при своем росте обращаются к источнику излучения, символом которого они и являются. Такое преображение с геометрической точки зрения возникает в момент начала сотворения, когда Единица становится Двойкой. Теперь, когда этот принцип включен в нашу геометрическую метафору сотворения, мы можем перейти к символу квадратуры.

Указанная на рисунке средневековая квадратура круга, построенная с помощью пентакля (пятиконечной звезды), символизирует достижение гармонии между интуицией (обозначенной пен- таклем) и разумом (обозначенным квадратом) или идею о том, что бесконечность (круг) информационно взаимодействует с человеческим интеллектом посредством законов гармонии.

Рисунок 7. 4. Данный рисунок основывается на указанных ниже соображениях:

Радиус окружности, описанной вокруг рта Ра, по теореме Пифагора равен: ф² = 1 + г² r = - 1 г = 4ф

и длина окружности равна 2п4ф, где^ф = 1, 272... и п = 3, 142..

2п4ф= 7, 993 для длины окружности или приблизительно 8.

Мы знаем, что сторона квадрата, описывающего исходную окружность, радиус которой равен

0, составляет 2. Таким образом, периметр этого квадрата равен 8 и поэтому приблизительно равен длине окружности круга, составляющей 7, 993.

Это дает величину числа п, которое использовалось древними египтянами для постройки Великой пирамиды:

2п4ф = 8 п4ф = 4 далее,

4ф= 4/п= 1, 272.

4^ф = п= 3, 1446056.

Тогда как истинная величина равна 3, 1415926. Практически точное значение числа пс использованием Золотого сечения составляет ф²х 6/5 = 3, 1416404. Отношение5: 6 или 1: 1, 2, между прочим, является функцией, которая связывает ф с п, а 1, 2 соответствует отношению 12 к

10. Двенадцать представляет собой число кругов космического времени, оно является числом завершения, и в виде отношения 6 к 5 оно связывает шестиугольник с пятиугольником.

Но вернемся к нашей фигуре: приняв четверть стороны квадрата (эта величина равна радиусу исходной окружности) за Единицу, мы можем определить эти величины: рп = V5/2 = 1, 118. = 1/2 + 1/ф В'п = В'К = A'M = ф= 1, 618.

OD = Оп= 1/ф = 0, 618.

AD = 1/ф² = 0, 3819.

ОМ = 4ф= 1, 2720196.

AF, НС = V(1 +1/ф²)= 1, 1756 = сторона пятиугольника DM= V2= 1, 4142135.

Рисунок 7. 5. Следующей нашей целью является построение квадрата, равного площади изначального круга.

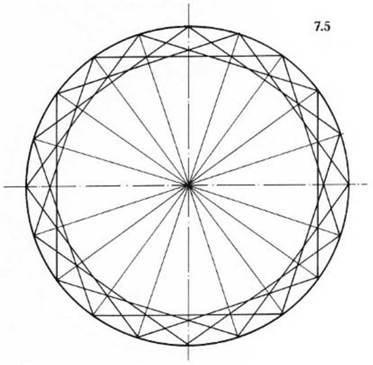
Впишите три дополнительных пятиугольника в круг, разделите пополам одну сторону пятиугольника, отметьте соответствующую точку на окружности, затем разделите пополам полученные сегменты. Эта операция дает начальные точки для трех новых пятиугольников, так что общее количество вершин составит 20.

Для нас это может служить символом сущностной пятеричной симметрии, расцвета принципа жизни в его возврате к свету, который проявляет себя через четверичную симметрию элементов природы: земли, воздуха, огня и воды.

Рисунки 7. 6, 7. 7, 7. 7а. Если мы начнем с точки А, в которой первый пятиугольник пересекает вертикальную ось, и проведем прямую линию

через вторую и пятую вершины пятиугольника до пересечения с вертикальной и горизонтальной осью (PQ), то получим первую сторону квадрата. Продолжая вычерчивание аналогичным образом, мы получим линии OR, ИБи SP. Используя геометрические методы расчета на пятиугольнике и его диагонали, приведенные в Рабочей книге 5, мы можем определить значения, приведенные на Рисунках 7. 7 и 7. 7а, и таким образом убедиться, что новый квадрат будет приблизительно равен по площади поверхности первоначального круга. Половина диагонали круга ОР = 1, 26006, а сторона квадрата PQRS = 1, 26006 х V2= 1, 7819938.

Этот способ представляет собой квадратуру, которая взята из конструкций Средних веков и которая не очень точна с математической точки зрения, но с символической точки зрения она обладает большой простотой и красотой. При заданных значениях сторона будет равна 1, 7819938, тогда как сторона более точного квадрата будет равна 1, 7724397, что дает разницу в

0, 0095548, при которой число сбудет равноЗ, 17.

 

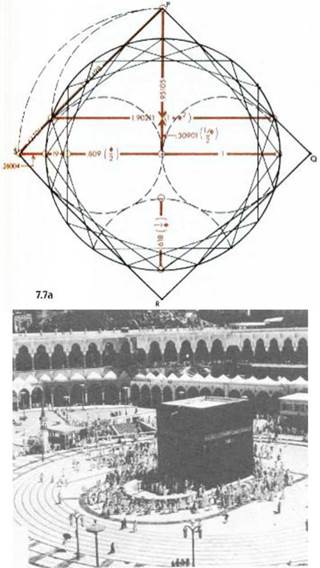
Хождение вокруг камня Каабы (что значит «куб») в Мекке является символическим ритуалом, относящимся к концепции Квад- ___________ ратуры круга. _____________________________________

Рисунок 7. 8. Объединив сделанные рисунки, мы увидим, что мандорла или рот Ра, на котором образуется первоначальный абстрактный (линеаризованный) квадрат, не касается, а скорее «излучает» вторую проявленную квадратуру (ту, которая относится к поверхности). Здесь, на одной диаграмме, мы видим классическое геометрическое соотношение, образованное между кругом и квадратом, междудуховным и материальным мирами. В следующем разделе мы обсудим то же самое отношение, но относящееся к объему: отношение между сферой и кубом.

VII. ОПОСРЕДОВАНИЕ: ГЕОМЕТРИЯ СТАНОВИТСЯ

МУЗЫКОЙ

Мы рассматривали деление единичности с помощью двух идей: функции корня (порождающий корень из 2 и возрождающий корень из 5), а также идеи о трех- и четырехчленной пропорциях, которые вытекают из указанных выше корней. В этом разделе мы объединим вместе идеи пропорции и корней, для того, чтобы до конца понять взаимоотношение между ними и вто же время показать, как эта окончательная геометрия становится основанием для музыкальной гармонии. Будем надеяться, что это прольет свет на слова Гете: «Геометрия - это застывшая музыка».

Наилучшим способом добиться этого является способ, который считается краеугольным камнем древней философской математики - наука опосредования, которая представляет собой простое наблюдение за функциями средних членов. Используя нашу дискуссию о трех- и четырехчленных пропорциях (стр. 44) в качестве отправной точки, давайте сначала обратим внимание на предупреждение Платона о том, что сравнения, основанные на четырех элементах, т. е. «разрывные четырехчленные пропорции», представляют по своей природе то, что он называет «конкретным знанием», которое носит уязвимый характер и открыто для оспаривания и произвола. Противоположностью этому является то, что он называет «основополагающим знанием», которое не является простым накоплением фактических или даже концептуальных данных, относящихся к объектам или явлениям, а заключается в осознании метафизических конструкций, посредством которых разум обладает способностью к постижению. Законы, которые управляют созиданием вещей, являются теми же законами, что и те, которые позволяют постичь эти вещи, а основополагающее знание представляет собой понимание этих законов. Такое знание можно получить, как говорит Платон, посредством изучения опосредования, которое представляет собой объединение двух крайних членов с помощью одного среднего члена. Мы рассмотрели это на примере с привлечением соотношений, состоящих из трех членов: а: b:: b: с, которые мы называем геометрической пропорцией, а греки называли логосом. Но этот простой пример представляет собой не только трехчленную пропорцию, так как наука опосредования изучает все суждения о пропорциональности, возможные между тремя членами не только посредством прямого пропорционального взаимоотношения, но также посредством взаимоотношений между разностями.

Опосредованную пропорцию можно определить как группу из трех неравных друг другу чисел, в которой разности между этими числами так относятся друг к другу, как одно из этих чисел относится к самому себе или к одному из двух других чисел.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: