 |
Комментарии к Рабочей книге 5 3 страница
|
|
|
|
Это странное краткое математическое «парадоксальное высказывание» содержит в себе формулу для трех основных средних: арифметического, геометрического и гармонического.
Давайте шаг за шагом рассмотрим это определение трех средних. Опосредованная пропорция образуется из группы любых трех чисел, в которойа больше чем о, а b больше чем с [а > b> с), такой, что «. разности между этими числами», т. е. а -Ь(первая разность) и Ь-с(вторая разность)
«. соотносятся друг с другом» а -b: b- с
«. так, как одно из этих чисел относится к самому себе» (случай 1): a -b: b-с:: a: a, b: b, с: с
«. или как одно из этих чисел к одному из оставшихся чисел»:
(случай 2) a-b: b- с:: а: Ьили (случай 3) а -b: b- с:: а: с.
В случае 1 выражение, решенное для среднего члена о, принимает вид b=(а+с)/2, что является общей формулой для арифметической пропорции. (Последовательность 3, 5, 7 представляет собой арифметическую прогрессию, арифметическое среднее которой b = 5.
В случае 2 выражение, решенное для среднего члена о, принимает вид V=ac или b = Vac, что является общей формулой для геометрической пропорции. Выражение 4, 8, 16 представляет собой геометрическую прогрессию, геометрическое среднее которой b = 8.
В случае 3 средний член о принимает вид b= 2ас/(а + с), а это является общей формулой для гармонической пропорции. Выражение 2, 3, б представля-етсобой гармоническую прогрессию, гармоническое среднее которой b = 3.
Такая формулировка опосредования дает нам общую формулу для всех наших основных математических операций. Арифметическая пропорция заключает в себе закон сложения и обратный ему (вычитание), а также описывает взаимоотношение, которое дает естественная последовательность количественных числительных: 1, 2, 3, 4, 5, 6... и т. д. Геометрическая пропорция заключает в себе закон умножения и обратный ему (деление) и описывает взаимоотношение, которое дает любая геометрическая прогрессия. Как мы уже говорили, сложение и умножение являются математическими символами для моделей роста. Гармоническое среднее получается при объединении первых двух; оно образуется путем умножения каких-либо двух крайних членов пропорции (а, с) с последующим делением полученного произведения на их среднее или арифметическое среднее (а + с)/2. Например, пусть унас есть два крайних члена 6 и 12, тогда произведение 6 и 12 = 72, арифметическое среднее 6 и 12 равно 9, и 72-=-9 = 8, так что 6, 8, 12 представляет собой гармоническую пропорцию.
|
|
|
Арифметическая: b = (а+с)/2 Геометрическая: b2 = ас Гармоническая: b = 2ас/(а+с)
Каждая пропорция обладает неким количеством характеристик, которые присущи исключительно ей. Например, арифметическая пропорция демонстрирует равенство разностей, но неравенство отношений. Так, в арифметической пропорции 3, 5, 7 7 - 5 = 5 - 3, но 7/5 не равно 5/3.
Геометрическая пропорция, с другой стороны, характеризуется равенством отношений, но неравенством разностей. Так в геометрической прогрессии 2, 4, 8 4/2 = 8/4, но 4 - 2 = 2 не равно 8 - 4 = 4.
Наиболее важной и мистической характеристикой гармонической пропорции является тот факт, что обратная к любой гармонической прогрессии представляет собой арифметическую прогрессию. Так 2, 3, 4, 5 представляет собой возрастающую арифметическую прогрессию, а обратная последовательность 1/2, 1/3, 1/4, 1/5 представляет собой уменьшающуюся гармоническую прогрессию. В музыке именно вставка гармонического и арифметического среднего между двумя крайними членами пропорции в удвоенных соотношениях - представляющих собой октаву
- дает нам прогрессию, известную как «музыкальная» пропорция: 1, 4/3, 3/2, 2. Другими словами, арифметическое и гармоническое среднее между удвоенными геометрическими соотношениями представляют собой численные соотношения, которые соответствуют тональным интервалам чистой кварты и чистой квинты-базовым созвучиям практически во всех музыкальных строях.
|
|
|
Основополагающая пропорциональная структура, которая содержит аксиомы для наших основных математических операций, также является основополагающей пропорциональной структурой для законов музыки. Давайте далее изучим роль этих трех пропорций как архетипических мыслительных форм для всей вселенной музыки.
Прогрессия 1, 4/3, 3/2, 2 отображает частоты основного тона, кварты, квинты и октавы. Затем мы найдем арифметическую и гармоническую пропорции между струной, длиной в 1 и 1/2, что представляет собой деление вибрирующей струны на два и порождает увеличение частоты, соответствующее октаве.
Музыкальная октава основывается на тоне, частота вибрации которого находится в точном соотношении 2: 1с другим тоном. Например, при игре на гитаре, ударяя по всей первой струне ЕХ, мы получим звучание основного тона, который в музыкальной системе обозначений обозначается через Е. Для облегчения расчетов давайте присвоим этому звуку величину в 6 единиц, обозначив, таким образом, количество его вибраций в секунду (в действительности оно составляет 82, 5). Затем, если мы прижмем наш палец на ладу, отмеченному буквой Е, и ударим по струне длиной Е'Х, которая составляет ровно половину длины ЕХ, то частота вибрации будет в два раза больше, чем у струны длиной EX. Мы получим численное значение в 12 единиц, которое образует соотношение 2: 1 с 6. Тон Е'Х = 12 называется октавой от Е. Звук октавы обладает необыкновенной характеристикой, заключающейся в том, что он имеет то же качество, что и основной тон и как бы растворяется в нем, хотя он определенно выше по высоте звука. Чувство, которое мы испытываем, слушая звучание октавы, включает всебя тайну одновременного присутствия одинаковости и различия. Качество постижения одинакового и различного представляет собой уравновешенность разума, что и должно развивать сакральная геометрия: качество, которое различимо явным образом, но составляет гармоническое целое. Аналогично, если мы прижмем палец на ладу, помеченном как В, и заставим звучать струну длиной ВХ, то воспроизведенный тон будет относиться к основному тону ЕХ как 3: 2 или, как мы это уже показали, как 9: 6. Этот тон В представляет собой красивый консонантный звук и называется квинтой, поскольку он является пятым тоном в естественной последовательности деление струны ЕХ: диатонической мажорной гамме, в которой Е является нотой до, а В - соль. Звукоряд включает в себя восемь таких естественных звуковых делений от Е до Е, отсюда и название октава Если мы прижмем наш палец к ладу, отмеченному буквой А, и дернем струну АХ, то она воспроизведет другой консонантный звук, называемый квартой, и его частота будет взаимосвязано с основным тоном как 4: 3 или, кок это уже здесь указывалось, как 8: 6.
|
|
|
Это дает прогрессию 1, 3/4, 2/3, 1/2, поскольку гармоническое среднее между 1 и 1/2 = 2/3, т. е. дает квинту, а арифметическое среднее между 1 и 1/2 = 3/4, т. е. дает кварту. При сравнении этих двух прогрессий мы видим инверсию соотношений и пересечение функциональных позиций арифметического и гармонического средних.
Тайна музыкальной гармонии, которая вырастает из одновременной инверсии, также содержит одновременное сложение и умножение. Октава от основного тона получается путем прибавления интервалов: кварта плюс квинта дают октаву, и перемножение частот вибрации кварты и квинты также даст значение октавы (4/3 х 3/2 = 2). Объединенное действие сложения и умножения в математике дает понятие логарифма, и, как мы уже увидели, Золотая пропорция является архетипом для этой формы роста.
В приведенной таблице в явном виде отображается тайна законов звука, которая заключается в том, что числа, рассматриваемые как отношения частот возрастающего звукоряда, равны длинам струны для нисходящей гаммы. Закон музыкальной гармонии, если его рассматривать с точки зрения идеи опосредованной пропорции, становится символом закона естественного порядка: Тао созданных миров, где противоположные, хотя и одновременные движения взаимодействуют для образования звука и формы.
|
|
|

Мы теперь можем наглядно представить этот числовой и гармонический принцип в виде геометрических фигур. Геометрическое среднее находится по формуле b2= ас;


Гармоническое среднее соответствует формуле Ь(а + с) = 2ас; т. е. произведение суммы крайних членов и среднего гармонического равно удвоенному произведению крайних членов, или
2ac
b =-------
a + b
Геометрическая пропорция называется совершенной пропорцией, поскольку она представляет собой прямую пропорциональную зависимость, соразмерность пропорции, связанной одним средним членом. Арифметическое и гармоническое средние образуют такое совершенство посредством замены разностей при изменении и инверсии.
Рабочая книга 8
Геометрия и музыка

Давайте теперь попробуем найти подтверждения того, о чем я говорил, в числовых прогрессиях. Обратимся сначала к геометрической последовательности: построим две геометрические последовательности (порядка 2): одну начнем с первого нечетного (мужского! числа после единицы - с 3, а другую начнем с первого четного (женского) числа - с 2. Отношение 1: 2 численно обозначает октаву, пространственное окружение, в котором первое консонантное деление на 3 (дающее кварту 2/3) символизирует посев, формообразующую функцию, которая вводит и определяет неизменные пропорциональные разделения в пределах первичного океана неразделенных звуков - в октаве:
3 6 12 24 48 2 4 8 16 32
В «Тимее» Платон показывает, что умножение на 2 и 3 дает нам все числа для пифагорейского строя путем последовательного умножения на квинту (3: 2). Будучи платониками, мы помним, что Двойка символизирует способность к множественности, символизирует октаву, женское начало, меняющийся сосуд, тогда как Тройка символизирует мужское начало, определенное, постоянное, дающее неизменную структуру, таблица умножения которой дает всю полноту музыки. Это была «музыка сфер», вселенские гармонии, озвученные этими двумя первичными символами мужского и женского начал.
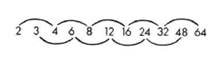
Теперь давайте объединим эти две геометрические последовательности, так чтобы они взаимодействовали по типу совокупления: Гармоническая
Арифметическая Мы можем видеть, что каждое второе пересекающееся множество из трех чисел дает нам поочередно арифметическую и гармоническую пропорцию: 2, 3, 4 представляет собой арифметическую пропорцию; 3, 4, 6 - гармоническую;
4, 6, 8 - арифметическую; б, 8, 12 - гармоническую и т. д. Таким образом, смешивание мужских чисел, порожденных геометрически, с женскими числами, также порожденными геометрически, дает нам возможность получения
двух чередующихся пропорций.

На этой диаграмме, выполненной Зорзи, показаны две прогрессии 2 и 3, указанные Платоном в Тимее; они показаны совместно с музыкальной пропорцией 6, 8, 9, 12. Музыкальная пропорция используется в качестве основы для порождения чисел в последовательности музыкальных октав, кварт и квинт, создавая, таким образом, гармоническую систему, которая могло бы использоваться в качестве модели в архитектуре, живописи и других искусствах.
|
|
|
Теперь давайте воспользуемся тем, что мы наблюдали при линейной организации, и посмотрим на ее формальную структуру с помощью Таблицы лямбда:

Итак, в Таблице лямбда, которую передал нам Никомах из Герата, содержится переплетение двух пропорций, дающее в итоге квадрат, который, как мы уже видели, является символом конечных, известных, проявленных сфер. Именно из этих чисел и музыкальных пропорций, как говорил Платон, сформирована Мировая душа.
Другой геометрический пример показывает взаимоотношение между корневыми функциями и принципами усреднения, которые создают мир гармонии в музыке.
Рисунок 8. 1. Взяв единичный квадрат, обе стороны и площадь которого равны 1, мы видим из геометрических соображений или при использовании тригонометрии, что, опустив перпендикуляр из точки пересечения V2 с V5/2 и продлив его до стороны (равной 1), мы разделим единичный квадрат, выступающий в роли единичности, в отношении 1/3 и 2/3, и, используя единичность в качестве большего члена, мы получим трехчленную арифметическую пропорцию: 1/3: 2/3: 1.
Выше приведена треугольная совокупность чисел, в которой пересекаются геометрическая прогрессия со знаменателем 2 (проходит горизонтально) и прогрессия со знаменателем 3 (идет по диагонали). Все последующие числа, расположенные по вертикали, относятся друг к другу как 2: 3, что аналогично умножению одного члена на 3/2 для получения значения стоящего внизу члена. Последовательное умножение на 3/2, т. е. квинту, представляет собой метод, использованный Пифагором для порождения музыкального ряда. Теперь становится очевидным происхождение числовых последовательностей, указанных на стр. 82 и 83.
Рисунок 8. 1. -: —: 1 Арифметическая пропорция
1 2
Порождающему характеру Таблицы лям-

бда придается особое значение на гравюре, выполненной по дереву в 1503 году и приведенной на стр. 7, где эта таблица изображена на бедрах женщины. При изучении таблицы мы можем видеть, что каждый квадрат в виде четырех чисел, например, 2, 4, б, 3, содержит внутри себя две арифметические прогрессии (прогрессию 2, 3, 4 и 2, 4, 6), что дает нам три стороны, образующие верхнюю часть и одну диагональ квадрата. На том же рисунке мы видим гармонические прогрессии 2, 3, 6 и 3, 4, 6, которые дают три стороны квадрата, две из которых накладываются на первую пропорцию, а другая дает четвертую сторону квадрата и другую диагональ.







Рисунок 8. 3. 1/ф: 1/ф2: 1 Геометрическая пропорция
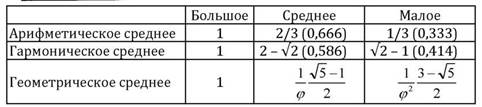

В таблице представлена аналогическая или геометрическая пропорция в соответствии с тем, как она отображается при делении на крайние и средние члены, но в пределах первоначальной единичности.
Все три средних значения получены при условии, что 1 является наибольшим из трех членов. Эта последовательность рассматривалась как форма трансцендентальных (надрациональных) пропорций, поскольку все они являются несоизмеримыми, содержащимися в изначальной Единичности. (Нужно помнить, что древняя музыка строилась только на отношениях целых чисел, но сам принцип музыкальной структуры относится к надрациональным разделениям Единичности. ) Эти три средних значения заключают в себе троицу троиц, три уникальных пропорциональных выражения, каждое из которых состоит из трех членов. Через сакральные корни из 2 и 5 они выражают фундаментальное гармоническое разделение Времени (музыки) и Пространства (геометрии) и часто использовались в традиционных культурах в качестве основ архитектуры, искусства, науки, мифологии и философии.
Рисунок 8. 4. На рисунке представлен способ изображения красивой пропорциональной чаши или сосуда в форме Грааля с использованием только гармонического разделения для получения ее кривых и размеров. Мы можем полагать, что это и является геометрической сутью Священного Граа
Рисунок 8. 2. Опять используя единичный квадрат и путем проведения дуги из нижнего правого угла, перенесем длину стороны, равную 1, в точку пересечения с диагональю V2. Затем проведем дугу из верхнего левого угла до пересечения с верхней стороной квадрата. Мы вновь получим точку на верхней стороне квадрата, в которой необходимо разделить квадрат, и такое разделение даст трехчленную гармоническую пропорцию: (V2 -
1): (2 - V2): 1.
Рисунок 8. 2. (V2 - 1): (2 - V2): 1 Гармоническая пропорция
Рисунок 8. 3. Последнее разделение стороны квадрата, равной 1, мы произведем с помощью диагонали V5/2. Для этого проведем дугу из точки пересечения, полученной при переносе половины стороны квадрата на диагональ V5/2, до пересечения с верхней стороной квадрата. Таким образом мы разделим квадрат в геометрической пропорции 1/ф: 1/ф2: 1.
ля.
В заданном квадрате ЛБСОсо стороной, равной 1, начертите его диагонали АС и BD. Радиусом ББиз центра в точкеВпроведите дугу DGдо пересечения с продлением стороны ВС для образования ВС = 2. Радиусом CGиз центра в точкеСначертите дугу GF. Радиусом ЛFиз центра в точкеАна- чертите дугу FBдля завершения половины профиля «Грааля». Проделайте те же операции с противоположной стороны.
Комментарии к Рабочей книге 8
Может быть потому, что постижение законов опосредования позволяет получить некоторое представление о фундаментальном взаимоотношении Музыки и Геометрии, Платон в своем Седьмом письме говорит, что опосредование более почитаемо, чем какое-либо другое получение знания. И, может быть, по той же причине египтяне построили две великих пирамиды в Гизе, одна из которых основана на пропорции 1, 4ф, ф - единственном треугольнике, стороны которого находятся в геометрической прогрессии, а у другой пирамиды стороны основаны на арифметической прогрессии 3, 4, 5. В наши дни СаймонУэйл говорит о важности изучения указанных пропорций, поскольку они служат основой христианского мистицизма.

Ознакомившись с работой Ханса Дженни, мы начинаем понимать взаимоотношение формы и звука в физическом мире. Эксперименты Дженни показали, что звуковые частоты обладают свойством объединения в правильные конфигурации хаотичных взвешенных частиц или организации эмульсий, находящихся в состоянии гидродинамической дисперсии, в упорядоченные, правильные периодические структуры. Другими словами, звук представляет собой инструмент, посредством которого временная структура частотных спектров может обретать правильные в пространственном и геометрическом отношении формы.
Планетарная система, основанная на музыкальной пропорции 6, 8, 9, 12 арифметическою и гармонического среднего между знаменателями геометрической прогрессии 6 и 12, вместе с другими тонами пифагорейского диатонического (основного) звукоряда

Звуковые частоты в этом эксперименте принуждают хаотически движущиеся частицы образовывать геометрически правильные формы.

СПРАВА. Геометрически симметричные фигуры получены при частотной интерференции электронного луча. Семилучевая фигура возникает из круга и вновь возвращается в него.
На этом рисунке для получения музыкальных соотношений объединены две важные фигуры: треугольник со сторонами 3, 4, 5 и Золотое сечение. Хотя мы и укажем последовательность создания этой диаграммы, все же мы не рекомендуем ее для начинающих геометров. Она основана на рисунке из книги «Божественная пропорция» Г. Э. Хантли.
Начертите окружность с центом в точке Ьи радиусом ЬА, проведите диаметр АС. Начертите линию, перпендикулярную АС и проходящую через точку А. Начертите дугу из центра А радиусом АС до точки F. Начертите линию из точки F, проходящую через центр Ьдо пересечения с окружностью в точке Н. Начертите линию из точки А, перпендикулярную FHи продлите ее до пересечения с окружностью в точке D.
Повторите то же самое для линии CB, перпендикулярной к FH. Начертите прямоугольник ABCD. (АВСДпредставляет собой прямоугольник со сторонами, относящимися как 1:
2, доказательство заключается в том, что ЬА- 1/2AF. Треугольник LJC подобен треугольнику LAF. JL= 1/2JC. ВА = 1/2ВС. )
Постройте треугольник со сторонами 3, 4, 5, проведя линию из точки F, которая касается окружности в точке D и продлите ее до пересечения с диаметром АС в точке Е. Доказательство того, что стороны треугольника равны 3, 4,
5, сделано по египетскому методу углового сложения: AFMи DFMоба равны и являются половинными углами (углы 1: 2).
1 1 (1 х 2) + (1х 2)_2 + 2 _4 AE = 4
Начертите окружность с центром в точке Jи радиусом JN.
Соотношение с малой стороной прямоугольника (АВ) = Единичность: МЬ= 1/2

НМ =JN = GJ= ф(при вращении радиуса (по- лудиагонали) LCвокруг точки Ьдо точки Н)
GM = JG + JM= ф+ 1=ф2 MN = MK = JN-JM= q> -1 = 1/ф KJ = JM-MK= 1 - 1/ф= 1 /ф2 GK = GJ + JK= ф+ 1ф2= 2
JO= 1/ф(вследствие подобия треугольников JKOи МКА)
В древнем Египте слуховое восприятие - т. е. прямой ответ на пропорциональные законы звука и формы - считалось эпистемологическим основанием философии и науки. Оно пробуждалось слепым арфистом, чья вошедшая в поговорку мудрость пришла не из видимого мира явлений, а из внутреннего видения метафизического закона.
Сегодня ряд современных наук подтверждает древнее космогоническое видение вибрационного сотворения с помощью Созидающего слова и Космического звука. Ален Данитлу указывает, что именно погруженность в такой таинственный взаимообмен между вибрацией и формой послужила основой для великих духовных культур прошлого:
«От атома и до вселенной каждое космическое движение обладает временем, ритмом, периодичностью и может быть сравнимо с вибрацией, а, следовательно, и со звуком, который является выражением ее природы. Не все вибрации воспринимаются нашими ушами, но отношения между ними можно сравнить со слышимыми частотами. Все атомы могут, таким образом, рассматриваться как формы энергии, которая проявляет себя через ритм, и все вещества ха-


JR =JG=ф
Если за единицу принимается единица измерения в треугольнике 3, 4, 5 вместо принятой до этого за единицу стороны прямоугольника 1: 2, то возникает вторая последовательность отношений фвместе с последовательностью отношений целых чисел, которые являются основными для образования музыкальных рядов:
Если AF = 3, а не л/5, и Единица = AF/3, то сторона прямоугольника 1: 2 = AF/AC= З/л/5 = 1, 3416.
Тогда RF= 3 х ф= 4, 854.
HF= 1/ф х 3 = 3/ф
рактеризуются конкретной взаимосвязью ритмов, которые могут формулироваться через взаимосвязь звуков. Именно по причине такого сходства между взаимосвязями звуков, с одной стороны, и формой и веществом природы, с другой стороны, возможны язык и музыка. Чистые звуки, нематериальные звуки, которые образуют содержательную природу вещей и которые Кабир называет «беззвучной музыкой», могут постигаться посредством приспособлений, которые более чувствительны, чем наши уши. Достижение такого восприятия является одной из целей упражнений таких любопытных физико-ментальных практик как йога».
(«Трактат по сравнительноймузыкологии») И сэр Джон Вудроф в своих переводах индусских текстов говорит:
«Естественное имя существа представляет собой звук, произведенный согласованным действием движущихся сил, которые образуют его. Именно поэтому говорится, что тот, кто мысленно или физически произносит естественное имя существа, дает жизнь существу, которое носит это имя».
(«Гирлянда писем»)
VIII. АНТРОПОС
Геометрическая космология, исследование которой мы проводим, является частью доктрины сотворения, известной как антропокосмизм, которая, в свою очередь, является фундаментальной для эзотерической традиции в философии, начиная с древнейших времен, и которая заново сформулирована в наше время Рудольфом Штайнером, РА. Шваллером де Любичем и другими. Первый принцип этой теории заключается в том, что Человек представляет собой не просто составную часть вселенной, скорее он является конечным итоговым продуктом эволюции и исходным зерном потенциальности, из которого началось зарождение вселенной. Мы можем воспользоваться аналогией между зерном и деревом: дерево вселенной является актуализацией зерна потенциальности, которым является Космический человек. В данном случае я использую слово Человек в том смысле, в каком на санскрите однокоренное с английским словом man слово manas означает «разум» или сознание, которое может размышлять о самом себе.
Тот же самый образ тождественности между зерном и деревом, между Космическим человеком и преходящим человеком на древе эволюции приводится в Книге Бытия. Для объяснения я воспользуюсь некоторыми идеями из книги Шифр Бытия автора-каббалиста Карло Суартса, перефразировав их в терминах антропокосмической мысли.
В главе 1 Бытия Адам помещен в сад со всеми уже созданными животными и растениями. Адам представляет собой обобщение или конечный этап эволюционного процесса. Это согласуется с парадигмой Человека как вместилища или конечного итога всего эволюционного развертывания, предшествовавшего ему.
В главе 2 Адам (теперь воспринимаемый как схематическая организация всего космического метаболизма) представляет собой перворожденное создание. В этой главе, которая вроде бы противоречит первой, Яхве-Элохим создает всех животных и показывает их Адаму, и Адам проходит испытание путем присвоения имени каждому из них. В этом испытании Адам узнаете каждой особи свое ответвление от собственного центрального пути. Он может дать им имя, поскольку знает их как самого себя. Адам является центральным стволом эволюционного дерева. Особи животных представляют собой сравнительно постоянные специализированные ответвления от пульсирующей сердцевины.
Видимое противоречие между главой 1 и 2 Книги Бытия находит свою параллель в современной эмбриологии, которая также дает нам две противоречивые теории развития человека: теорию «итога» и теорию «неотении». Первая теория, которая соответствует главе 1, представляет собой теорию о том, что животные повторяют фазы взрослого организма своих предков во время эмбрионального и послеродового роста. Поэтому человеческий эмбрион проходит через все основные эволюционные этапы, которые предшествовали ему: не только через этапы развития млекопитающих, рептилий, рыб и растений, но также (на ранних стадиях клеточного деления) и все этапы развития правильных геометрических тел. Неотения, тем не менее, предлагает фактически противоположный взгляд, который соответствует главе 2 Книги Бытия. Эта теория основывается на том факте, что существует свыше двадцати важных характеристик тела, которые являются общими для человека и примата, но у приматов они проявляются на стадии эмбриона или молодой особи, а затем исчезают. Физически люди представляют собой преждевременно рожденных приматов, у которых указанные физические черты были гормонально заторможены или прерваны.
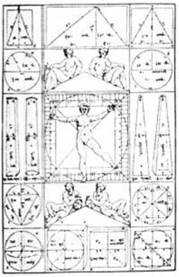
Когда Адам дает имена различным особям, он узнает или, как мы должны сказать, припоминает свое собственное эмбриональное прошлое (подведение итога). Но он также осознает себя пылающим зерном, первичной моделью всего органического процесса вселенской жизни (неотении). Адам в этот момент сотворения может объявить: «Я не вижу ничего, что не является мной;
Идея Космического человека повторяется в современной науке в виде концепции голограммы, которая показывает, что каждый фрагмент целого содержит элементы всей структуры целого. В то же время, будучи конкретным компонентом целого, он проявляет себя кок индивидуум. В древней науке метафорическое применение понятия антропо- косма служило основанием для астрологической философии, его также можно обнаружить в алхимии в виде поиска философского камня: части, в которой можно найти целое. Во времена Ренессанса при рисовании тела человека соблюдались важные пропорции вселенских геометрических форм и музыкальных отношений. На рисунке мы видим корреляцию между \ 2 и воспроизводящим органом человека.
Я не вижу ничего, что, взятое вместе, подобно мне». Так Адам проходит испытание. Он не ограничивается своей самоидентификацией с последовательными этапами эволюции, связанными с минералами, растениями и животными, и в тоже время идентифицирует себя с высшей силой при организации космической энергии, с непроявленной геометрией зерна-идеи.
Вместе со своей идентификацией с первоначальной вселенской природой Адам готов к своей инкарнации в качестве Адама Кадмона, материализованного Космического или Божественного человека.
Ведическая традиция передает то же антропокосмическое видение, но с более метафизической позиции. Она говорит нам о том, что Бог создал вселенную из-за своего желания увидеть себя и восхищаться собой. Бытие такого непостижимого Бога может рассматриваться как все- сознающее, все-содержащее, всемогущее, однородное, бесконечное расширение чистого, бесформенного духа. Его желание увидеть себя сотворенным (или отделенным от себя самого) в виде Идеи самого себя называется в индийской мысли реальностью-идеей. Такое божественное само- восприятие, «созидающее слово» в иудейско-христианской мысли, само это явление является Космическим человеком. И такой Космический человек является тем, что мы, обыкновенные люди, называем Вселенной.
|
|
|


