 |
Комментарии к Рабочей книге 5 4 страница
|
|
|
|
Сотворенная вселенная затем рассматривается как питающая плацента, посредством которой такая Божественная самоидея воплощает себя или инкарнирует: создает бытие, облекшееся в материю, для того, чтобы стать воспринимаемым и обожаемым. Эта позиция противоположна нашему обычному мышлению. Человечество не рассматривается как ребенок или продукт матери-земли, а, скорее, земля является основополагающим свойством, содержащимся в образе Космического человека.
Антропокосмическая философия представляет эволюцию как непрерывный инверсионный обмен между вечным Космическим человеком и эволюционирующим человечеством. Вселенское бытие скручивается в плотную семя-форму самого себя. В принципе это наблюдается в царстве минералов: в крайней степени бессознательное, неизменное сгущение. Такое семя затем вызывает противоположное движение эволюции. Наступает черед мира растений, который стремится вверх, за пределы ограничений; он одушевляет, высвобождает и воплощает в себе божественные качества, которые были заперты или заключены в минерале.
Эти божественные качества, проявляющие себя и выделяющиеся как функциональные принципы и этапы роста в мире растений - а именно корень, стебель, листья, цветы, плод, семя, - мы можем рассматривать как символы-аналоги для всего вселенского процесса Становления.
Затем возникает мир животных в виде инверсии к растительному процессу, и здесь мы можем обнаружить альтернативный ритм инволюции (скручивания) и эволюции, который служит источником последующих миров. Животные вновь «привлекают» принципы, действия и жизненные функции, которые растения «развили» или открыли, прояснили и возвысили. С помощью такой инволюции животные достигают способности к индивидуальной мобильности, которая является необходимой предшественницей индивидуальной воли. Инволюция может рассматриваться как материализация духа, а эволюция - как одушевление материи.
|
|
|
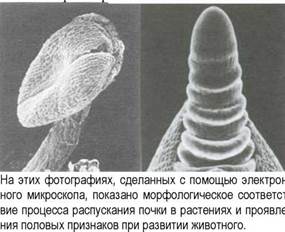
Рудольф Штайнер дает эффектный образ такого процесса, заметив, что человек в его животном теле является в действительности ничем иным как вывернутым наизнанку растением. Респираторную функцию в растении выполняет лист. Эта функция выполняется открытыми солнцу листьями, расположенными на внешних окончаниях в соответствии с принципом ветвления. У человека респираторная функция выполняется легкими, ветви которого находятся в нем самом.
Продолжая аналогию, мы можем увидеть, что цветок, который являетсяполовым органом растения, растет вверх и тянет энергию растения вверх, к свету, тогда как у человека и животного половые органы направлены вниз ипритягивают энергии тела в этом же направлении. Корни растений находятся в земле, у человека характерная корневая функция обнаруживается визвилинах мозга, который пустил корни в небесах мысли и ментальных энергий. Ментальный процесс представляет собой процесс переваривания, ассимиляции и преобразования, который функционирует как более высокая, чем у желудочно-кишечного, переваривающего процесса, частота, как вид желудочнокишечного тракта, который также имеет извилистую форму. Таким образом, последовательность миров в физическом мире, начиная с минералов до растений, от них - к животным, становится символом постоянного движения инволюции и эволюции одного Бытия, которое разделено на взаимодополняющие качества духа и материи.
В рамках логики такого видения эволюции, целью физического человека является трансформация его текущей животной инкарнации в тело света, как это происходит при эволюции растения из инволюционного мираминералов. Посредством концепции Человека, отождествляемого с Космосом, концепции антропокосмизма, сакральная геометрия становится космограммой, изображающей драму такого божественного рождения. И во временавсех эпох строительства храмов сакральная архитектура, основанная на такой геометрии, была книгой, раскрывающей эту вечную драму.
|
|
|
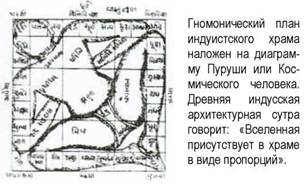
В Индии все еще жива традиция Ваступурушамандала- традиция проектирования храмов, в основе которой - Космический человек. Мы также обнаружили, что архитектурная модель для великих готических соборов представляла собой вселенского Христа-человека на кресте сотворения. В Египте существует один большой храм, построенный по образцу человеческой фигуры. Это - храм Луксор, в котором Космический человек представлен и в архитектуре, и на ритуальных барельефах в процессе своего рождения. Индусская архитектурная сутра говорит: «Вселенная присутствует в храме в виде пропорций».
В наше время наблюдается сближение новой биологической науки, основанной на кибернетике и теории информации, и мистической доктрины антропокосмизма. С эволюционирующей вселенной вокруг и внутри нас можно соприкоснуться только посредством наших чувственных органов. Поэтому наш мозг и тело неизбежно формируют все наши восприятия и сами формируются теми же видимыми и невидимыми энергиями, которые создают каждую воспринимаемую вещь. Тело, Разум и Вселенная должны обладать своей созидательной самобытностью. Выражение «Человек, познай себя» было принципом древней науки, каким оно постепенно становится и в науке современной. Процитируем физика Роберта Дайка:
Правильный образ мыслей не соответствует выражению: «Вот вселенная, а каким должен быть человек? » Вместо этого мы должны спросить: «Вот человек, а какой должна быть вселенная? »

(Цитируется по книге К. У. Мизнера, К. С. Торна, Д. А. Уиллера «Гравитация»)
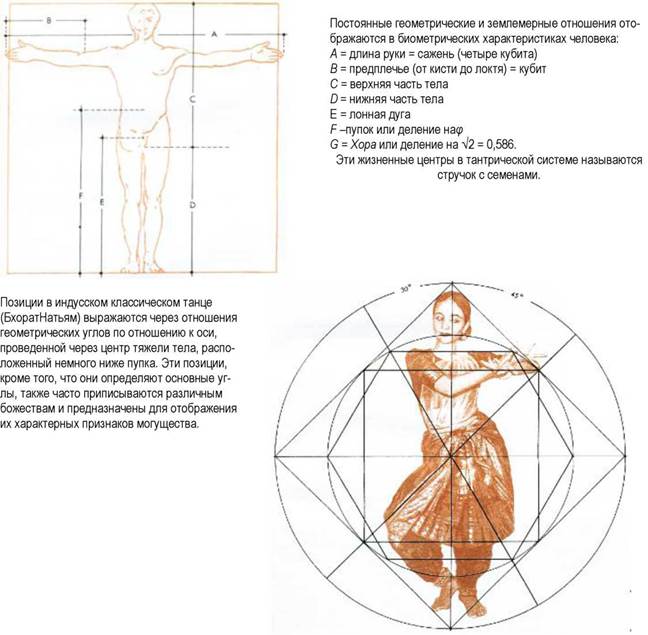
Человеческое тело в своих пропорциях содержит все важные геометрические и землемерные функции и системы измерений. Древнеегипетский кубит, который представляет собой пространственно-временную пропорциональную меру длины (1/1000 часть расстояния, которое земля по экватору проходит за одну секунду при вращении), фут, морская сажень, древнеегипетский эквивалент метра, - все эти Отношение куба к вписанной сфере меры длины соизмеримы с размером или дви
|
|
|

жением земли. Отношение фзадается пупком. Идеальные пропорции человека предполагают, что отношение длины руки к общей длине тела соответствует отношению между хордой и дугой в 60°. Длина верхней части тела (выше вертлюжной впадины) так относится к общей длине тела, как объем сферы относится к объему описанного вокруг нее куба (1: 1, 90983).
Кроме того длина верхней части тела относится к длине лонной дуги как п/3: 1 или 1, 047: 1. Так, пропорции идеального человека сосредоточены в центре круга неизменных космических отношений.
Посредством отождествления с важными вселенскими пропорциями, выраженными с помощью формы такого идеального человека, каждый отдельно взятый человек может поразмыслить над связью между его собственной физиологией и вселенской космологией и, благодаря этому, представить свою собственную связь с вселенской природой. Эта совокупность универсальных пропорций в теле Идеального человека становится во многих цивилизациях основой для выработки критериев (канонов), которые регулируют размер песнопений и стихов, движений в танце и пропорций в ремеслах, искусстве и архитектуре.
Человек и Крест как основа замысла плана собора. В философии храмовой архитектуры храм должен олицетворять образ Парадигматического человека, высший архетип, который эманирует из себя весь мир.

X. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ПРОСТРАНСТВ
Восприятие объема дает другую метафору для первоначального и вечно продолжающегося созидающего акта материализации Духа и создания форм. Сам древний миф о сотворении, происходящий из города Гелиополиса, расположенного в Египте, дает пример такого способа воображения. Нун, Космический океан, символизирует чистое, непроявленное дух-пространство без границ и формы. Он предшествует любому распространению, любой конкретности, любому божеству. Он является чистой потенциальностью. Через семя или желание Создателя, который скрыт в этом океане Нун, неразделенное пространство приходит в движение, для того чтобы сжаться и сгуститься с образованием объема. Так Атум, создатель, сначала создает или выделяет себя из неопределенного Нун путем создания объема, для того чтобы начался процесс сотворения.
|
|
|
Какую же форму мог иметь этот первый объем? Какие объемные формы являются наиболее важными? Существует пять объемных форм, которые считаются наиболее важными, поскольку они являются единственными формами, у которых все ребра и все внутренние углы равны между собой. К ним относятся тетраэдр, октаэдр, куб, додекаэдр и икосаэдр, и они являются отображением в объеме соответственно треугольника, квадрата и пятиугольника: 3, 4, 5. Все другие правильные объемные тела получаются путем усечения этих пяти. Эти пять тел называются Платоновыми, потому что предполагается, что Платон уже был знаком с ними, когда писал «Тимея» - диалог, в котором он дает обзор космологии с использованием плоскостной геометрии и геометрии тел. В этом диалоге, который, по сравнению со всеми остальными работами Платона, носит наиболее ярко выраженный пифагорейский характер, он доказывает, что четырьмя базовыми элементами в мире являются земля, воздух, огонь и вода, и что каждый из этих элементов соотносится с одной из пространственных фигур. Традиция связывает куб с землей, тетраэдр с огнем, октаэдр с воздухом и икосаэдр с водой. Платон упоминает «некое пятое построение», использованное создателем при сотворении вселенной. Так додекаэдр стал ассоциироваться с пятым элементом: эфиром (праной). Устроитель вселенной Платона установил порядок из первобытного хаоса этих элементов с помощью основополагающих форм и чисел. Приведение в порядок в соответствии с числом и формой на более высоком уровне привело к предначертанному расположению пяти элементов в физической вселенной. Основополагающие формы и числа затем стали действовать в качестве границы раздела между высшим и низшим мирами. Сами по себе и в силу своей аналогии с другими элементами, они обладали способностью формировать материальный мир.
Как отмечает Гордон Пламмер в своей книге «Математика космического разума», индусская традиция связывает икосаэдр с Пурушей. Пуруша представляет собой семя-образ Брамы, высшего создателя самого себя, и в качестве такового этот образ представляет собой карту или план вселенной. Пуруша является аналогом Космического человека, антропокосмизма западной эзотерической традиции. Икосаэдр представляет собой очевидный выбор для этой первой формы,
|
|
|

Пять правильных Платоновых тел.
НА ПРЕДЫДУЩЕЙ СТРАНИЦЕ. Пять правильных многогранников или Платоновых тел использовались, и были известны задолго до времени Платона. КейтКричлоу в своей книге «Время остановилось»дает убедительное свидетельство тому, что они были известны людям неолита Британии, по крайней мере, за 1000 лет до Платона. Это заявление основывается на наличии ряда сферических камней, хранящихся в музее Ашмолин в Оксфорде. Эти камни, размеры которых соответствовали тому, что можно уместить в руке, были покрыты геометрически точными сферическими фигурами куба, тетраэдра, октаэдра, икосаэдра и додекаэдра, также как и некоторые дополнительные сложносоставные и псевдоправильные тела, такие как кубо-октаэдр и ико- додекаэдр. Кричлоу говорит: То что у нас ель, представляет собой объекты, несомненно указывающие на степень математических способностей, которые до сих пор отрицались в отношениичеловека неолита некоторыми археологами или историками математики. Он размышляет о возможной связи этих объектов со строительством больших каменных номических колец в Британии, относящихся к той же эпохе: «Изучение небес связано, кроме всего прочего, с роботами со сферой, которые требуют понимания сферических координат. Если жители неолита Шотландии построили МейсХауи до того, кок пирамиды были построены древними египтянами, то почему бы им не изучать законы трехмерных координат? Не является ли то, что Платон, а также Птолемей, Кеплер и Аль-Кинди приписывали космическое значение этим фигурам, не более, чем совпадением? » Одновременно Люси Пейми в ее ожидаемой книге о ской системе мер приводит доказательство того, что ем о данных пяти телах обладали уже в Древнем царстве Египта.
Рабочая книга 9
Платоновы тела
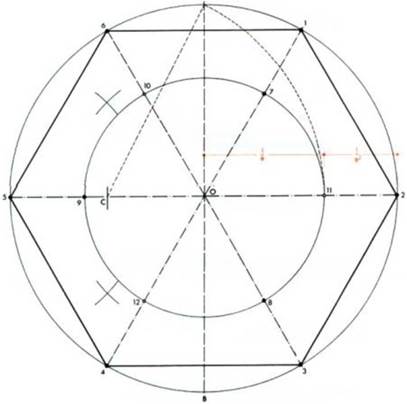
Рисунок 9. 1. Одновременное образование Платоновых тел в икосаэдре. Начертите окружность радиусом ОАи впишите в нее шестиугольник (2, 5) со стороной ОА=
1. Проведите вертикальный диаметр АВ. Пометьте каждую вершину шестиугольника цифрами с 1 до 6 и начертите три диагонали 1-4, 2-5, 3-6. Из центра в средней точ- кеСрадиусом СА начертите дугу до пересечения с радиусом 0-2 в точке 11. Линия СА = V5/2 разделит радиус 0-2 в соотношении 1/ф и \/ф2. Начертите окружность радиусом 0-11 и в местах, где эта окружность пересекает радиусы шестиугольника, сделайте пометки в виде точек и пронумеруйте их с 7 до 12.
Рисунок 9. 3. Внутри сферы,

кость: 10-6-7-2-11, центральная ось которой проходит по диаметру через точку 4. ) Повторите то же самое с точками 5, 6, 1, 2 и 3, обращайтесь к Рисунку 9. 2 как к наглядному примеру. Из точки 8 проведите «лучи» 8-12, 8-5, 8-6, 8-1 и 811. Повторите то же самое с точками 9, 7, 11, 12 и 10.
обозначьте икосаэдр только с помощью его 12 точек. Начертите все связи между 12 вершинами, опустив те из них, которые проходят через центр сферы. Видно, что из каждой точки к противоположной точке можно провести максимум 5 «лучей».
Например, из точки 4 проведите линии 4-10, 4-6, 47, 4-2 и 4-11. (В действительности 5 противоположных точек будут задавать правильную пятиугольную плос-
Рисунок 9. 2. Точки 7, 8 и 9 образуют одну из 20 граней икосаэдра. Эта грань, как и другие 19, представляет собой равносторонний треугольник, показанный здесь в точной пропорции, поскольку он параллелен плоскости рисунка. Грани 7, 8, 2; 8, 9, 4; 9, 7, 6; и 6, 7, 1; 1, 7, 2; 2, 8, 3; 3, 8, 4; 4, 9, 5; и 5, 9, 6 завершают 10 граней, непосредственно видимых нашим глазам. Точки 10, 11, 12 обозначают другую плоскость, видимую в точной пропорции. Она расположена непосредственно напротив плоскости 7, 8, 9, но скрыта от глаз, как и другие 9 плоскостей, отмеченных на рисунке прерывистыми линиями.

Можно видеть, что с помощью ф, «божественного семени», икосаэдр обретает форму.
радиус которой равен радиусу круга из предыдущего рисунка,
Все множество таких «лучей» будет пересекаться группами по 3 луча в 20 точках пересечения. Эти 20 точек являются вершинами, которые задают додекаэдр, «подвешенный» внутри более крупного икосаэдра. Здесь показаны для ясности шесть видимых граней из 12.

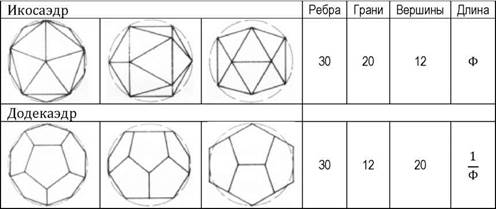
Возникновение додекаэдра происходит спонтанно, как результат естественного пересечения всех внутренних точек- источников икосаэдра. Эти две фигуры являются обратными друг другу: обе состоят из 30 ребер, но, несмотря на это, икосаэдр имеет 20 граней и 12 вершин, а додекаэдр 12 граней и 20 вершин.
Рисунки 9. 4, 9. 5. Создание додекаэдра автоматически дает нам готовый куб, который определяется 8 вершинами додекаэдра и ребрами, совпадающими с диагональю каждой грани. На рисунке видна верхняя грань 1,
2, 3, 4 и две боковые грани 3, 4, 5, 6 и 1, 4, 5, 7. Диагонали граней этого куба образуют переплетенный или звездообразный тетраэдр. Звездообразный тетраэдр состоит из двух тетраэдров с вершинами, направленными в противоположные стороны; именно эти два тетраэдра и сплетены друг с другом.

Объем, занимаемый этими двумя тетраэдрами, задает ок-

таэдр, что таким образом и завершает эту группу, состоящую из правильных многогранников.
На рисунке куб полностью включает в себя звездообразный тетраэдр. Октаэдр, как и куб, звездообразный тетраэдр и икосаэдр, виден здесь в двумерной перспективе, в плоскости, в виде шестиугольника. Только додекаэдр не входит в наружный контур шестиугольника.
Не только проекции внутренних радиусов икосаэдра образуют ребра додекаэдра, но и аналогично проекция радиуса додекаэдра дает ребро икосаэдра. Такое попеременное получение проекции одной формы из другой здесь обозначено только в виде линий без геометрического доказательства, которое вполне можно провести.
Давайте на словах повторим то, что мы проделали с помощью геометрии. Если мы соединим все внутренние вершины икосаэдра, нарисовав три линии из каждой из них, соединяющих каждую вершину с ей противолежащей, и затем из двух верхних вершин проведем четыре линии к двум противоположным, так чтобы эти линии сошлись в центре, мы, действуя в соответствии со сказанным, естественным образом построим ребра додекаэдра (смотрите Рисунок 9. 1 и 9. 2). Такое построение происходит автоматически при пересечении внутренних линий икосаэдра. После создания додекаэдра мы можем, просто используя шесть из его вершин и центр, построить куб. Используя диагонали куба, мы можем построить звездообразный или переплетенный тетраэдр. Пересечения звездообразного тетраэдра с кубом дают нам точное местоположение для построения вписанного октаэдра. Затем в самом октаэдре с использованием внутренних линий икосаэдра и вершин октаэдра получается второй икосаэдр. Мы прошли через весь полный цикл, пять этапов от семени к семени. И такие действия представляют собой бесконечную последовательность.
Если размер стороны куба равен 1, то сторона внешнего икосаэдра будет равна 4, а у додекаэдра длина стороны будет равна 1/ф. Длина стороны у переплетенных тетраэдров будет равна V2. Длина стороны октаэдра составит 1/V2, а сторона нового маленького внутреннего икосаэдра будет равна 1/ф2: ошеломляющее созвездие гармоний! Отец (Пуруша) дал рождение самому себе.
Единственным ключом, который необходим, для того чтобы начать такое рисование, является метод, с помощью которого необходимо знать, как находить вершины первого икосаэдра. Он дается нам на радиусе окружности и является результатом деления на ф.
Комментарии к Рабочей книге 9
Индусы представляли себе Пурушу как не проявленного и не затронутого сотворением, точно так же как на рисунке икосаэдр не соприкасается с другими телами. Додекаэдр рассматривался как Пракрити, женская сила созидания и проявленности, Вселенская мать, квинтэссенция естественной вселенной. Этот додекаэдр соприкасается со всеми телами сотворения, находясь внутри своего тихого, наблюдательного партнера. Переплетенный тетраэдр рассматривается как сочетание инь и ян, поскольку тетраэдр представляет собой пространство троичности и поэтому является первичным символом функции, сопровождаемой ей обратной. Результатом такого гармонического пересечения противоположностей является куб, символизирующий материальное существование, четыре состояния материи: землю, воздух, огонь, воду. И куб, и переплетенный тетраэдр соприкасаются с додекаэдром. В самом сердце этого тетраэдра находится октаэдр, и поскольку куб образован на его вершинах, октаэдр символизирует кристаллизацию, статичное совершенство материи. Это - алмаз, сердце космического тела, трансформированные и очищенные линзы света, двойная пирамида. Внешнее продвижение, которое распространяется во все более обширные миры, разграничивает само себя, свое сотворение: икосаэдр, Пуруша, который порождает додекаэдр, Практрити, а внутри Пракрити - полная свобода проявленного существования. Сгущение начинается с помощью секретного семени, которое сжимает круг, бесконечный неразделенный дух в икосаэдре. Семя - это фи, огонь духа.
Трансцендентные принципы: икосаэдр и додекаэдр, Пуруша и Пракрити, первичнаядуаль- ность - каждый обладает пропорцией фи. Но когда мы подходим к уровню естественного мира противоположныхдуальностей - инь и ян - и к кубу материи, и его кристаллизации в октаэдре, здесь появляется корень из 2, который и вступает в действие. Корень из 2 представляет способ, посредством которого ф действует в природе. И из октаэдра, очищенного состояния материи, его кристаллизации в драгоценных камнях, возрождается икосаэдр, его размеры пропорциональны фи: 1/ф2. Эта пропорция 1/ф2 = 0, 382. представляет собой геометрическую функцию, связываемую с Христом (смотрите стр. 63). Будучи квадратом, она выражает проявленную форму, Сына, и будучи стороной внутреннего икосаэдра, она представляет собой инкарнацию или точный образ первоначального, образующего икосаэдра, Отца, Пурушу, Антропокосма.
роде. В своих идеальных формах они существуют только на метафизическом уровне как чистые креативные идеализации и могут быть отображены только посредством гео- Два куба поваренной соли метрии, только тогда сознание способно усвоить их

К
Моноклиническая система гипса
УХ
Гексагональная система берилла
Трехгранная система кварца
идокраза
Хлорит в кварце
Мир минералов отображает чистую геометрию тел с особой ясностью, но при этом важно помнить, что них тел не существует в при

Пуруша и Пракрити представляют собой вечную созидательную дихотомию в индусской мифологии. Пуруша является антропокос- мическим, парадигматическим Человеком или Семенем, которое создает Пракрити, вечную пленительную Женственность, для того, чтобы ее чрево дало жизнь его собственному овеществлению в мире форм.


Толкование солнечной системы, данное Кеплером, представлялось в виде одного платонового тела, размещенного в другом; радиусы взаимодействующих концентрических сфер соответствуют орбитам планет
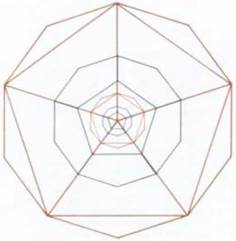
НА СЛЕДУЮЩЕЙ СТРАНИЦЕ. На ном рисунке правильные многогранники определяются девятью концентрическими окружностями, расположение которых дает всю необходимую информацию для поп роения этих тел. Каждое тело находится в простом гармоническом взаимоотношении с другими телами, именно эти трансцендентные функции V2, /рИ ^образуют указанные модели взаимоотношений. Как и на предыдущем рисунке, все эти тела возникают одновременно. Но в данном случае, если удалить одну из концентрических окружностей, вся структура не сможет воспроизвести оставшиеся тела. Это является образом великой буддистской идеи о взаимозависимом порождении архетипических принципов сотворения.
Эти символические объемные тела образно воспроизводят нашу космическую историю и превосходно отображают колоссальные движения, значение которых они передают. Суть заключается в постоянном обмене между икосаэдром, мужским началом, Пурушей, и додекаэдром, женским началом, Пракрити. Икосаэдр представляет собой фигуру с 12 вершинами и 20 гранями. Он является структурой, состоящей из треугольников: три является динамическим «мужским» числом. Андрогинный додекаэдр, как источник жизни, имеет 12 граней и 20 вершин и представляет собой фигуру, в основе которой лежит число пять, число жизни (мужское число 3 + женское число
1). Звезда, рожденная внутри пятиугольника додекаэдра, представляет собой конфигурацию Космического человека, улучшающего жизнь, Золотую пропорцию.
Те же пять правильных тел в соответствии с классической традицией рисуются таким образом, что они содержатся в девяти концентрических окружностях, и каждое тело соприкасается со сферой, которая описана вокруг следующего тела, расположенного внутри ее. Такая композиция проявляет немало важных взаимоотношений и заимствована из дисциплины, называемой coapotransparente, относящейся к восприятию сфер, изготовленных из прозрачного материала и
размещенных одна в другой. Такое наставление давалось Фра Лукой Паччоли многим великим людям Ренессанса, включая Леонардо, Брунуллески и Зорзи.


Фра Лука Паччоли, величайший учитель сакральной геометрии времен Ренессанса. Сосредоточение внимания ученика на прозрачных телах было способом, который должен был помочь увидеть метафизические реальности за рамками всех их внешних проявлений.
Существует мнение, что в индусской метафизике каждое из тел представляет собой символ одного из невидимых тонких конвертов, которые, как предполагалось, окружают и взаимодействуют с физическим телом человека. Эта традиция связывает

небольшой, расположенный в центральной части икосаэдр с окончательным Совершенством Тела в его физическом проявлении; октаэдр - с физическим или Питающимся телом (местом, где расположен инстинктивный разум);
тетраэдр - с прановым или Энергетическим телом (местом, где расположена интуитивно-ментальная способность); куб - с телом Сознания «чистого разума»;
додекаэдр - с телом Знания (местом, где расположено врожденное знание о тождественности);
икосаэдр - с телом Блаженства (то, что относится к медитации).
В заключение мы можем задать вопрос: как упражнения по сакральной геометрии могут помочь нам справиться со сложными вопросами существования: Какова природа Духа? Какова природа Сознания? Какова природа Тела?

Мои личные геометрические упражнения дают на это ответ: Тело является наиболее сконцентрированным проявлением Сознания, а Сознание представляет собой все тонкие продолжения Тела; и в основании всего мира, от наиболее сконцентрированного до наиболее тонкого, лежит одно вещество. Этим веществом является Дух, который очаровывает красотой геометрических построений.
На фотографии показан эффект преломления с максимальным увеличением, которое может позволить себе наука в отношении природы атомного вещества, представляющего собой геометрически организованные структуры света-энергии.
БИБЛИОГРАФИЯ
Acts of John, The, Apocrypha ofthe New Testament.
Aurobindo. Sri, The Life
Divine, Centenary Edition, vols 18, 19, Pondicherry, India, Sri AurobindoAshram Trust,
1970.
Beckmann, Petr, A History of Phi, New York, St Martin's Press, 1971.
Boyer, Carl В., 'Zero, the Symbol, the Concept, the Number', National Mathematics Magazine. Brunts,
Tons, The Secrets of
AncientGeometry - and its Use,
2 vols, Copenhagen, Rhodos, 1%7.
Charpentier, Louis,
TлеMysteriesofChartres Cathedral (trs. SirRonald Fraser), London, Research into LostKnowledge Organization, 1972.
Colman, Samuel, N. A.,
Nature'sHarmonic Unity, New York, Putnam's, 1912.
Critchlow, Keith, Islamic Patterns, London, Thames & Hudson, New York, Schocken, 1976.
---, Order in Space,
London, Thames & Hudson, 1969, New York, Viking, 1970 ---, Time Stands Still,
London, Gordon Fraser, 1979, ForestGrove (Ore. ), International Scholarly BookService, 1980.
Danitlou, Alain, Traitk demusicology comparke, Paris, 1959.
---, Hindu Polytheism,
BollingenSeries LXXIII, New York. Pantheon Books, 1%4. Danzig, Tobias, Number, theLanguage 4 Science, New York, The Free Press, 1967.
De Nicolbs, Antonio, Avatara, NewYork. Nicolas Hays, 1976.
Fabre d'olivet, Antoine, LaMusigue expliguke commescience el comme art, Collection Delphica, Lausanne, Aged'Homme, 1972.
Fournier des Corats, D.,
LaProportion kgyptienne et lesrapports de divine harmonie, Paris, Editions Vega, 1957.
Ghyka, Matila, Esthhique
desproportions dans la nature etdans les arts, Paris, Gallimard, 1933. -, The Geometry 4 Art and Li/e. New York, Dover, 1977.
---, Le Nombre d'or, 3 vols, Paris, Gallimard. 1931.
Gillings, Richard J., Mathematicsin the Time of the Pharaohs, Cambridge (Mass. ), London. MITPress, 1972.
Gutnon, Rent, Les Principes ducalcul infinitksimal, Paris, Gallimard, 1946.
Hambidge, Jay, The Elements ofDynamic Symmetry, New York, Dover, 1967.
Heninger. S. K., Jr., Touches
ofSweet Harmony, San Marino, California, Huntington Library, 1974.
Jenny, Hans, Cymaticc I and
11, Basel, Basilius Press, 1974.
Kramrisch, Stella. The
HinduTemple, 2 vols, Delhi, MotilalBanarsidass Press.
1976.
Levarie, Siegmund, and
ErnstLevy, Tone: A Study in MusicalAcoustics, Kent State University Press, 1968.
McClain, Ernest, The Myth ofInvariance, New York, NicolasHays, 1976; Boulder (Col. ), London, Shambhala, 1978.
---, The Pythagorean Plato:
Preludeto the Song Itself, New York, Nicolas Hays, 1978.
Menninger, Karl, NumberWords and Number
|
|
|


