 |
P = lim ΔΦ/ΔS – гидростатическое давление в точке при ΔS → 0
|
|
|
|
Рср = Φ /S
Рср – называется средним гидростатическим давлением
Р = Δ Φ /Δ S – напряжение
P = lim Δ Φ /Δ S – гидростатическое давление в точке при Δ S → 0
Размерность давления в [ Н/м2, Па ]. Окружающий нас воздух действует на нас давлением, которое называют атмосферным:
Ратм = 1т. атм = 9, 81 Н/см2 = 98100 Н/см2[Па] = 98, 1 кН/м2 [кПа]
Свойства гидростатического давления.
Давление в точке обладает тремя свойствами:
1. Гидростатическое давление в точке действует нормально к площади его воспринимающей и являющееся сжимающим, т. е. оно направленно внутрь того объема жидкости, давление на который мы рассматриваем.
В движущейся жидкости при наличии касательных напряжений возникла бы необходимость доказывать это свойство. Здесь же ее нет.
2. Величина давления в рассматриваемой точке не зависит от ориентации площадки, т. е. как бы не располагалась площадка давление всегда направлено к ней нормально.
3. Гидростатическое давление в точке зависит от ее координат в пространстве. Это свойство специального доказательства не требует, т. к. ясно, что по мере погружения точки под уровень жидкости давление будет возрастать, и наоборот.
Р = φ (х, у, z)
Лекция №2
Дифференциальные уравнения равновесия
жидкости (ур. Эймра). Поверхности равного
давления. Основные уравнения и закон
гидростатики.
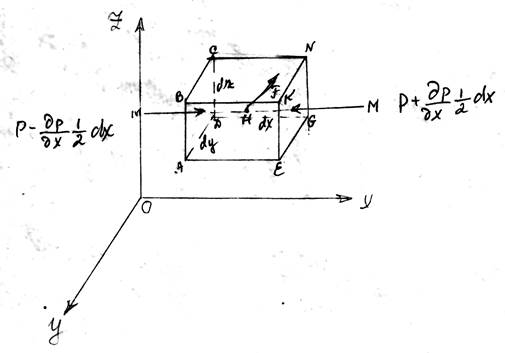
Выделим в жидкости, находящийся в равновесии, элементарный параллелепипед со сторонами dx, dy, dz и центром Н. Рассматриваемый объем находящийся в равновесии под воздействием:
|
|
|
- поверхностных сил давления, направленных внутрь параллелепипеда нормально к его граням;
- объемных (массовых) сил, действующих на каждую частицу жидкости.
Р – гидростатическое давление в т. Н. Учитывая непрерывность изменения давления в жидкой среде и пренебрегая величинами бесконечно малыми, стремящихся к нулю при уменьшении выделенного объема до размеров точки, определим среднее гидростатическое давление на соответствующих гранях; изменение величин давления, приходящихся на единицы длинны ММ представим частной производной σ P/σ x.
На грани АВСD действует давление: P - σ P/σ x ½ dx; на грани EKNG: P+ σ P/σ x ½ dx.
Сила давления определяется соответственно как произведение давления в центре тяжести на площадь действия этого давления.
Массовая сила dF=dm . j, проекция этой силы по координатным осям Fx, Fy, Fz; dm=ρ dx dy dz.
Составим уравнение равновесия в направлении оси ОХ, из которого следует, что проекция всех сил, действующих на выделенный объем, в направлении любой оси (например ОХ) равна 0:
(P - σ P/σ x ½ dx) dy dz – (P+ σ P/σ x ½ dx) dy dz + Fxρ dx dy dz = 0
Разделим почленно данное уравнения (т. е. приведем каждый члем к единице массы) на dm = ρ dx dy dz и получим:
Fx – 1/ ρ σ P/σ x = 0
1/ρ σ P/σ x – единичная поверхностная сила, σ P/σ x – градиент изменения давления.
Очевидно, что для любого избранного направления:
Fн – 1/ρ σ P/σ x = 0
Можем записать систему уравнений, которая называется общим условием равновесия жидкости:
Fx – 1/ρ σ P/σ x = 0 dx
Fy – 1/ρ σ P/σ x = 0 dy
Fz – 1/ρ σ P/σ x = 0 dz
Получена эта система в1755 году членом Российской академии наук Леонардом Эймром.
Умножим полученые уравнения на dx dy dz и сложив их получим:
|
|
|
Fx dx + Fy dy + Fz dz = 1/ρ (σ P/σ x dx + σ P/σ x dy + σ P/σ x dz)
Т. к. Р = φ (х, у, z), то выражение в скобках справа представляет собой полный дифференциал давления:
dP = ρ (Fx dx + Fy dy + Fz dz)
Это уравнение называют дифференциальным уравнением равновесия жидкости.
Физический смысл этого уравнения: поверхностные силы равны массовым.
Поверхность равного давления.
Поверхностью равного давления в жидкости называется поверхность, все точки которой испытывают равное давление.
Уравнение такой поверхности мы можем получить из основного уравнения равновесия жидкости, полагая P=const или dP = 0
Поверхность уровня на границе жидкой и газообразной сред называется свободной поверхностью.
Положение свободной поверхности зависит от сил, действующих на жидкость.
Свободная поверхность покоящийся жидкости
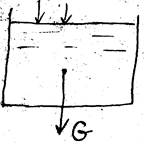
Из всех объемных сил на жидкость действует только вес, тогда Fx = 0; Fy = 0; Fz = 0
Дифференциальное уравнение будет представлено в виде:
|
|
|


