Лекция №6

                       Уравнение Д. Бернулли для реальной жидкости:

                       элементарной струйки и потока. Общие понятия

                                 потерях напора. Основные уравнения установившегося

                                 равномерного движения жидкости.

Для элементарной струйки реальной жидкости.

Вязкая жидкость испытывает сопротивление при движении, поэтому часть удельной энергии вдоль струйки теряется. Следовательно необходимо учитывать эту потерю. Обозначим ее через Δ Е_1-2 и запишем полученное ранее уравнение в следующим виде:

gZ₁ + P₁/ρ + u₁²/2 = gZ₂ + P₂/ρ + u₂²/2 + Δ Е_1-2 или в виде напоров:

Z₁ + P₁/ρ g + u₁²/2g = Z₂ + P₂/ρ g + u₂²/2g + Δ Н_1-2, здесь Δ Н потеря напора

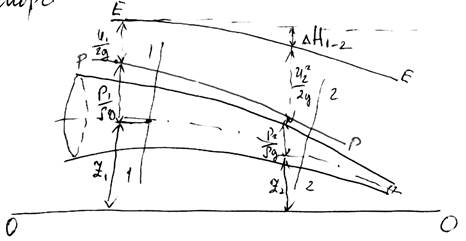
Линия ЕЕ соответствует гидродинамическому напору, а линия РР – гидростатическому или потенциальному напору.

Обозначим расстояние между сечениями Δ ℓ, отношение Δ Н к Δ ℓ называют средним гидравлическим уклоном:

Y = d (Z + P/ρ g + u₂ /2g ) / dℓ, этот уклон характеризует положение напорной линии и всегда положительный.

i = d (Z + P/ρ g) / dℓ - пьезометрический уклон, характеризующий положение пьезометрической линии. Он может быть как положительным, так и отрицательным.

 

Для потока реальной жидкости.

От уравнения Д. Бернулли для элементарной струйки реальной жидкости можно перейти к уравнению для потока если принять следующие допущения ( поток – совокупность элементарных струек):

1. О распределении давлений в живых сечениях потока. Наметим два сечения 1-1 и 2-2 (в потоке они плоские):

Опытами установлено, что если в сечении пометить несколько точек и вывести из них пьезометры, вода в них установится на одной отметке. Аналогичная картина будет для любого сечения в направлении движения жидкости.

Z и P / ρ g = counst

 

Можно сказать, что давление в конкретном сечении потока распределяется, подчиняясь гидростатическому закону при параллельно-струйном и плавно-изменяющимся установившимся движении.

 

2. Неравномерность распределения скоростей.

Задача учета неравномерности распределения скоростей по живому сечению сопряженных с определенными трудностями, поэтому в гидравлике все расчеты ведутся по средней скорости: U = Q/W

Рассмотрим эпюры действительных и средних скоростей:

 

При наложении этих эпюр видно, что действительный скорости неравномерно распределяются по отношению средней скорости, т. е.

u = U ± U₀, где U₀ – отклонение действительно скорости от средней.

Рассмотрим поток как совокупность элементарных струек. Энергия каждой отдельной струйки:

dE = (Z + P / ρ g + u²/2g) ρ gdQ

Энергия всего потока может быть найдена суммированием этих энергий:

 

Е = ∫ _w(Z + P / ρ g + u²/2g) ρ gdQ = ρ g ∫ _w(Z + P / ρ g) dQ + 0, 5 ρ g/g ∫ _w u²dQ

 

Первое слагаемое выражений потенциальную энергию потока. Полагаясь на первое допущение эта энергия определяется:

 

ρ g ∫ _w(Z + P / ρ g) dQ = ρ g (Z + P / ρ g) ∫ _wdQ = ρ g Q (Z + P / ρ g)

Е_пот = ρ gQ (Z + P / ρ g)

 

Второе слагаемое выражает кинетическую энергию в сечении:

 

Е_кин = 0, 5 ρ ∫ _w u²dQ;  dQ =udw; u = U + U₀

E_кин = 0, 5 ρ ∫ _w u³dW=0, 5 ρ ∫ _w (U + U₀)³dW=0, 5 ρ ∫ _w (U³+3U²U₀ + 3UU₀² + U₀³) dW

 

Интеграл суммы представим в виде суммы интегралов и определим каждый из них:

E_кин = 0, 5 ρ (∫ _w U³dW + ∫ _w 3 U²U₀dW + ∫ _w3UU₀² dW + ∫ _wU₀³dW) ∫ _w U³dW;

∫ _w 3 U²U₀dW = 3 U² ∫ _w U₀dW = 0, т. к. U₀±;

 

∫ _w= U₀³dW ≈ 0, как величина третьего порядка малости;

E_кин = 0, 5 ρ (U³W + 3U∫ _wU₀ ² dW), вынести за скобку U³W;

 

Е_кин 0, 5 ρ U³W (1 + 3U∫ _wU₀ ² dW) / U³W

Е_кин = 0, 5 dU^{2 .} U ^. uρ = ρ dU²/2 Q = ρ g (dU²/2g) Q; Е_кин= ρ gQ (dU²/2g)

 

Энергия в сечении потока равна Е_пот + Е_кин;

Е = ρ gQ (Z + P/ ρ g) + ρ gQ (dU²/2g), разделив почленно правую часть на ρ gQ, получим:              Е = Z + P/ ρ g + dU²/2g

 

Записав энергию для двух сечений получим уравнение Д. Бернулли для потока:

Z₁ + P₁/ ρ g + dU₁²/2g = Z₂ + P₂/ ρ g + dU₂²/2g + h_1-2, h_1-2 – потеря напора.

 

Уравнение Д. Бернулли выражает особый закн сохранения энергии:

d = Е_{кин u}/ Е_{кин U} = 1, 05/1, 1 и показывает неравномерность распределения действительных скоростей.

 

Общие понятия о потерях напора

Z₁ + P₁/ ρ g + dU₁²/2g = Z₂ + P₂/ ρ g + dU₂²/2g + ∑ h_1-2

∑ h_1-2 =∑ h_е +∑ h_м,  где h_ℓ – потеря напора по длине; h_m – потеря напора в местных сопротивлениях.

Потеря напора по длине

h_ℓ = λ ℓ /d U²/2g, где λ – коэффициент сопротивления трению; ℓ - длина участка трубы; d – ее диаметр; U²/2g – скоростной напор. Эта зависимость Дарси – Вейстаха. Коэффициент λ зависит от вида сопротивления, в котором работает труба и является функцией:

λ = β (∆ э, R_e), где ∆ э – эквивалентная шероховатость трубы, зависящая от ее материала и чистоты обработки; R_e – число Рейнольдса   R_e=Ud/v 

 

Различают три зоны сопротивления:

I зона – ламинарного или вязкостного сопротивления.

В любой зоне из-за небольших скоростей течения у стенок трубы образовывается неподвижный слой жидкости, закрывающий шероховатость трубы и λ зависит от числа Рейнольдса: λ = 64/R_e;

II зона – переходная, практического применения не имеет;

III зона – турбулентного режима, которая делится на три область сопротивления:

- область гидравлически гладких труб, в этой области неподвижный слой больше выступов шероховатости и λ также зависит от числа R_e:

λ = φ (R_e); λ = 0, 316 / R_e ^{0, 25}; формула Блазиуса

- область доквадратического сопротивления, в которой с увеличением скоростей течения жидкости частично оголяется шероховатость трубы и λ зависит: λ = φ (∆ э, R_e) и определяется по формуле А. Д. Альтмуля:

λ = 0, 1 (1, 46∆ э/d + 68/ R_e)^{0, 25}

- область квадратического сопротивления или интенсивного перемешивания. Здесь полностью разрушается неподвижный слой жидкости и λ = φ (∆ э), определяется по формуле Б. Л. Шифринсона:

λ = 0, 11 (∆ э/d)^{0, 25}

Существует целый ряд эмпирических зависимостей для определения λ, их находят в справочной литературе.

Для определения области сопротивления необходимо сравнить число Рейнольдса с его граничными значениями:

R^| _{е гр.} = 10d/∆ э    и    R^|| _{е гр.} = 500d/∆ э

- область гидравлически гладких труб    

R_е < R^| _{е гр.} = 10d/∆ э

- область доквадратического сопротивления;

10d/∆ э = R^| _{е гр.} < R_е < R^|| _{е гр.} = 500d/∆ э

- область квадратического сопротивления

R_е > R^|| _{е гр.} = 500d/∆ э

 

Потеря напора в линейных сопротивлениях

Линейными сопротивлениями называют преграды на пути движения потока.

Все местные сопротивления можно объединить в 4 группы

1. Сопротивления изменяющие направление потока: плавные и резкие повороты трубопровода (колена).

2. Сопротивления изменяющие размеры живого сечения потока: резкое сужение и резкое расширение

3. Различного рода запорные устройства (краны, вентили, задвижки и т. д. ) и дополнительная арматура на трубопроводе (сетки, змеевики и т. д. )

4. Сопротивления связанные с отделением или присоединением части потока.

 

Опредляются потери в местных сопротивлениях по формуле Вейсбаха:

h_м = ζ U²/2g, где ζ – коэффициент местного сопротивления.

Этот коэффициент зависит от вида местного сопротивления и его размеров (помещены коэффициенты в гидравлических справочниках)

Лишь для резкого расширения в 1748 году Борда получил теоретическую зависимость для определения потерь напора:

h_{p . p} = (U₁ – U₂) / 2g, где U₁ – скорость в узком сечении, U₂ – в широком; (U₁ – U₂) – называют потерянной скоростью.

 

Основное уравнение установившегося равномерного движения жидкости.

Цель задачи:  Найти зависимость потерь напора по длине от величины сил трения внутри жидкости.

Движение рассматриваем:

1. Установившееся

2. Плавноизменяющееся

3. Равномерное, т. е

W₁ = W₂ = W = const; U₁ = U₂ = U = const.

 

Для вывода уравнения воспользуемся законом количества движения.

Изменение количества движения равно сумме проекций всех сил, действующих на выделенный объем жидкости, на направление оси движения NN.

В случае равномерного движения изменение количества движения равно нулю.    (KD) = mv; m = ρ Q.

Выделим внешние силы, действующие на объем жидкости, ограниченной сечениями 1-1 и 2-2.

1. Собственный вес объема

G = Wℓ ρ g, где W – площадь живого сечения, ℓ - расстояние между сечениями.

Проекция веса на направление движения NN:

G_N = Wℓ ρ g sin θ, где ℓ sin θ = Z₁ – Z₂ G_N = ρ gW (Z₁ – Z₂ )

2. Силы давления F₁ и F₂ действуют по пюруам выделенного объема:

F₁ = P₁W a F₂ = P₂W   

Эти силы проектируют без искажения

3. Проекция на ось NN нормального давления на боковую поверхность (силы парные) равна нулю.

4. Силы трения

- силы внутреннего трения между слоями парные и равны нулю

- силы внешние (о стенки трубы)

Т₀ = τ ₀ ^. ℓ ^. x, где τ ₀ – касательные напряжения, ℓ - расстояние между сечениями, х – смоченный периметр.

Т₀ проектируется на направление движения без искажения.

G_N + F₁+ F₂ – T = 0

ρ gW (Z₁ – Z₂ ) + P₁W – P₂ W - τ ₀ ^. ℓ ^. x = 0

Разделим почленно полученное уравнение на ρ gW:

(Z₁ – Z₂ ) + P₁/ρ g – P₂ /ρ g - τ ₀ ^. ℓ ^. x / ρ gW = 0

Перегруппируем члены уравнения:

(Z₁ + P₁/ρ g) - (Z₂ + P₂/ρ g) в случае равномерного движения эта разница равна потери по длине h_ℓ

h_ℓ = τ ₀ ^. ℓ ^. x / ρ gW; R = W/x, тогда x/W = 1/R

h_ℓ = τ ₀ / ρ g ℓ /R – это уравнение показывает зависимость потерь напора от силы трения.

h_ℓ /ℓ = Y, тогда уравнение перепишется в виде:

YR = τ ₀ / ρ g – основное уравнение равномерного движения.

Потери напора по длине для заданной жидкости прямопропорциональны  касательным напряжениям силы трения Т₀.

 

  

 

 

 

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: