Лекция №8

 

                                     Математические зависимости для

                                               турбулентного режима. Истечение жидкости

                                              через малые отверстия и насадки.

 

Законы распределения скоростей при турбулентном режиме.

 

Опытами установлено следующее:

1. Скорости у стенок трубы равны нулю (т. к. образуется неподвижный ламинарный слой).

2. На небольшом расстоянии от стенки скорости достигаю т значения мало отличающихся во всех точках живого сечения.

3. Средняя скорость в сечении равна:

U = (0, 7 / 0, 9) U_max

Принимая во внимание линейную зависимость пути перемешивания ℓ и расстояние от стенки y, т. е. ℓ = χ y, воспользуемся уравнением касательных напряжений

τ = ρ ℓ ² (du/dy)²

du = (√ τ /ρ ) dy/ℓ = (√ τ /ρ ) dy/χ y; √ τ /ρ = u_*, где  u_* - динамическая скорость в м/c.

du = u_*  dy/χ y, интерпретируя это уравнение, получим:

u = (u_*/χ ) ℓ u y + C

Скорости у стенок трубы изменяются по логарифмическому закону.

Определим постоянную интегрирования С, полагая y = z, u = u_max

C = u_max - (u_*/χ ) ℓ u r

u = (u_*/χ ) ℓ u y + u_max - (u_*/χ ) ℓ u r

u = u_max + u_*/χ (ℓ u y - ℓ u r)

Мы получили закон распределение скоростей по живому сечению потока при турбулентном режиме.

Чем больше число Рейнольдса, тем больше выравнивание скоростей:

R_e = 2700 U = 0, 75 U_max

R_e = 10⁸ U = 0, 9 U_max

R_e → ∞ U → U_max

Потери напора при турбулентном движении

 

Воспользуемся уравнением установившегося равномерного движения:

τ = ρ gRY

и решим его относительно Y:

Y = τ / ρ g 1/R

Исходя из опытов Шези: τ / ρ g  = KU², где К – коэффициент пропорциональности равный: К = 1/С², где С – коэффициент Шези.

τ / ρ g = U²/C², тогда уклон Y будет равен:

Y = 1/C² U²/R, где R = d/4 из этой зависимости получим U = C√ RY

Y = 4/C² U²/d, c = √ 8g/λ -  формула Шези, здесь λ – коэффициент сопротивления трению.

Поставим в зависимость, полученную для уклона Y, C и домножим левую и правую часть на ℓ:

Yℓ = 4λ /8g  ℓ U²/d; h_e = λ (ℓ /d) U²/2g

При турбулентном режиме потери напора по длине пропорциональны длине участка и квадрату скорости.

 

Истечение жидкости из малого отверстия в тонкой стенке при постоянном напоре.

 

Н – геометрический напор

Если диаметр отверстия d составляет 0, 1Н, такое отверстия называю малым.

U_a ≈ U_в

Под термином тонкая стенка понимают такую стенку:

1. Края стенки заострены и поток касается только кромки.

2. Толщина стенки ∂ < 0, 2 d

 

При истечении жидкости через отверстие в тонкой стенке линии тока в плоскости самого отверстия непараллельны друг другу, поэтому движение резкоизменяющееся. На некотором расстоянии от отверстия кривизна линии тока уменьшается, его называют сжатым W_c. Это происходит на расстоянии ℓ ≈ 0, 5 d. Сжатие сечения характеризуется коэффициентом сжатия E = W_c/W₀, a W_c = EW₀.

Цели задачи:

1. Определить скорость в сжатом сечении;

2. Найти расход через малое отверстие Q

Выберем два сечения 1-1 и С-С и запишем для них уравнение Д. Бернулли:

Z₁ + P₁/ρ g + dU₁²/2g = Z₂ + P₂/ρ g + dU₂²/2g + h_1-2

Z₁ = Н;   P₁/ρ g = P₂/ρ g; dU₁²/2g ≈ 0, т. к. площадь живого сечения 1-1 больше площади сечения отверстия (Ω > > W).

Z₂ = 0, P₂/ρ g = P_a/ρ g; dU₂²/2g = dU₂²/2g; h_1-2 = ζ U_c²/2g,

где коэффициент сопротивления, учитывающий потери в местном сопротивлении; d = 1, 0.

Н + P₀/ρ g = P_a/ρ g + U_c²/2g + ζ U_c²/2g;

Н + (P₀/ρ g - P_a/ρ g) = Н_пр приведенный напор; в случае открытого сосуда Н_пр = Н.

Н_пр = (1+ ζ ) U_c²/2g → U_c = 1/√ (1+ ζ ) √ 2g Н_пр

Обозначим 1/√ (1+ ζ ) = ς – коэффициент скорости отверстия, учитывающий потерю напора

U_c = ς √ 2gH_кр или U_c = ς √ 2gH  ς = U_g/U_теор

Определим расход в сечении:

Q = W_c ^. U_c = EW₀ ς √ 2gH_пр.

Q = Eς W₀ √ 2gH_пр.

Обозначим E ς = μ – коэффициент расхода

Q = μ W₀ √ 2gH_пр

Q = μ W₀ √ 2gH

μ = Q_д / Q_теор

Различают два вида сжатия потока:

1. Полное, когда струя сжимается воздухом по всему периметру

2. Неполное – часть периметра отверстия примыкает ко дну, которое является направляющей плоскостью для потока.

Полное сжатие струи делится на совершенное и несовершенное:

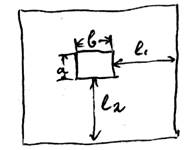
1. Совершенное - ℓ ₁ > 3в; ℓ ₁ > 3а

2. Несовершенное сжатие наблюдается при более близком расположении отверстия к направляющим стенкам: ℓ ₁ < 3в; ℓ ₁ < 3а

Коэффициент расхода для несовершенного сжатия выше. сем для совершенного.

В случае совершенного сжатия для круглого и прямоугольного отверстий:

Е = 0, 62 / 0, 64

ς = 0, 97

ζ = 0, 06

μ = 0, 060 / 0, 62

 

Истечение жидкости через насадки

 

Насадком (насадкой) называется короткая труба, присоединенная к малому отверстию в тонкой стенке.

ℓ = (3/4) d

Насадки бывают:

1. Цилиндрические: внутренние и внешние

2. Конические: сходящиеся и расходящиеся

3. Коноидальные

Рассмотрим внешний цилиндрический насадок. При входе в него струя претерпевает сжатие на расстояние ℓ, а далее расширяется и выходит из насадки полным сечением.

В сжатом сечении давление меньше атмосферного.

Запишем уравнение неразрывности для сечений С-С и 2-2:

 

W_c V_c = W₂ V₂ → U_c = W₂U₂/W_c → U_c = (1/E) U₂ , т. е. U_c > U₂,

 

а в сечении 2-2 давление равно атмосферному, из закона сохранения энергии, следует, что в сечении 2-2 давление меньше атмосферного. Т. о. можно делать вывод, что в сечении С-С выкуум. Вакуум зависит от напора Н.

За счет вакуума внешний цилиндрический насадок обладает большей пропускной способностью по сравнению с отверстием (на 32%).

Запишем уравнение Д. Бернулли для сечений 1-1 и на выходе из насадка 2-2:

Z₁ + P₁/ρ g + dU₁²/2g = Z₂ + P₂/ρ g + dU₂²/2g + ∑ h_1-2

Z₁ = Н;  dU₁²/2g ≈ 0;  Z₂ = 0; ∑ h_1-2 = ζ U_c²/2g + λ ℓ /d (U_c²/2g)

Н = dU₁²/2g + ζ U_c²/2g + λ ℓ /d (U_c²/2g) = dU₁²/2g (d + ζ + λ ℓ /d)

U₂ = 1 /(√ d + ζ + λ ℓ /d) √ 2gH

 

Потери в насадке: на стадии струи, на расстоянии, по длине и относятся к скоростному напору на выходе.

U₂ = ς _H √ 2gH

Т. к. на выходе струя претерпевает сжатия и E = 1, 0, μ _H = ς _H; ς цилиндрического насадка 0, 82

Q = ς _HW₂√ 2gH = μ _H W₂√ 2gH

 

Величина вакуума в насадке зависит от действующего напора, который складывается из Н и h_вак. Допустимая величина вакуума, т. е. будет засасывается воздух из выходного отверстия.  h_вак ≈ 0, 75 Н.

 

Конически сходящийся насадок

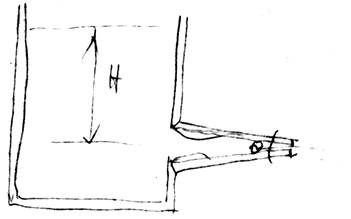
Коэффициент расхода такого насадка зависит от угла схождения θ Е=0, 946 при θ = 13⁰ ς = 0, 97

Вакуум отсутствует, это объясняется уменьшением потерь напора за счет плавного входа струи в насадок. Обладает большой скоростью на выходе, с увеличением θ до 50⁰ коэффициент расхода уменьшается.

 

Конически расходящийся насадок

В этом насадке скорость в сжатом сечении значительно больше, чем в цилиндрическом насадке и возрастает с увеличением угла расхождения (конусности).

Потери в этом насадке значительно больше, что обусловлено значительным расширением струи и неблагоприятными условиями входа в насадок.

 

 

Е = 1, 0, μ _Н = ς _Н = 0, 50

 

Расход в конически расходящимся насадке увеличивается по сравнению с другими насадками за счет большой величины вакуума.

Принимаем для увеличения пропускной способности при малых скоростях на выходе (при пожаротушении).

 

 

 

⇐ Предыдущая12345678910

Поделиться:

Воспользуйтесь поиском по сайту: