Лекция №7

                                 Два режима течения жидкости:

                                ламинарный и турбулентный, их особенности.

                               Число Рейнольдса. Математические зависимости

                                для вышеназванных режимов.

В природе существуют два вида движения: слоистый (упорядоченный) или ламинарный и турбулентный (неупорядоченный). Наиболее полно эти виды движения исследовал английский физик О. Рейнольдс в 1883 г.

 

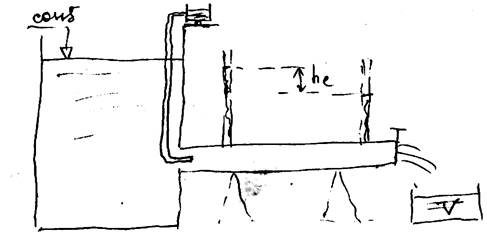
Q = V/t м³/с

U = Q/W м/с

 

 

В результате опытов было установлено, что переход от ламинарного к турбулентному течению происходит при скорости, называемой критической. Эта скорость для труб разных диаметров различна, а так же она возрастает с увеличением вязкости жидкости и уменьшается с уменьшением диаметра трубы.

1. Ламинарный режим

2. Переходный режим

3. Турбулентный режим

Число Рейнольдса R_e

В результате опытов Рейнольдс установил общие условия существования ламинарного и турбулентного режимов.

Режим потока зависит от величины безразмерного числа, учитывающего основные факторы, определяющие это движение: U, d, ρ b и абсолютную вязкость μ.

Это число Рейнольдса: R_e = Udρ / μ = Ud/v; или R_e = Uℓ /v

С физической точки зрения R_e представляет собой меру отношения кинетической энергии объема жидкости к работе сил трения. Кинетическая энергия пропорциональна ρ ℓ ³U², а работа сил трения - μ ℓ ³U

R_e = ρ ℓ ³U²/ μ ℓ ³U = Uℓ /v; ℓ - линейный параметр.

Можно сказать, что число Рейнольдса представляет собой отношение сил инерции к силам вязкости.

Число Рейнольдса, при котором происходит смена режимов, называется критическим. Для круглых труб R_e = 2320, для сечений отличных от круглого R_e = 580. Величина R_{e кр} зависит от условий входа потока в трубу, шероховатости стенок и др.

При R_e <  R_{e кр} режим ламинарный, при R_e > R_{e кр} – турбулентный.

Для каждого из режимов установлена зависимость потерь напора от скорости:

h_{e л} = В_л U

h_{e т} = В_т U^m, где m от 1, 75 до 2, 0

В – коэффициент пропорциональности, зависящий от размеров трубопровода и свойств жидкости; m – tg угла наклона каждой из зависимостей к горизонту: m_л = 1, 0; m_т = 1, 75 / 2, 0

 

Распределение скоростей по сечению для круглой трубы при ламинарном режиме.

Рассмотрим установившееся движение при ламинарном режиме полагая, что начальное сечение потока находится на достаточном расстоянии от входа для обеспечения устойчивого распределения скорости в поперечном сечении.

Ламинарное движение (слоистое) характеризуется силой трения, напряжение которой τ определяется законом внутреннего трения Ньютона:

1. τ = μ du/dy, где u – местная скорость течения

С другой стороны τ можно определить из уравнения равномерного движения:

2. τ = ρ gRY

 

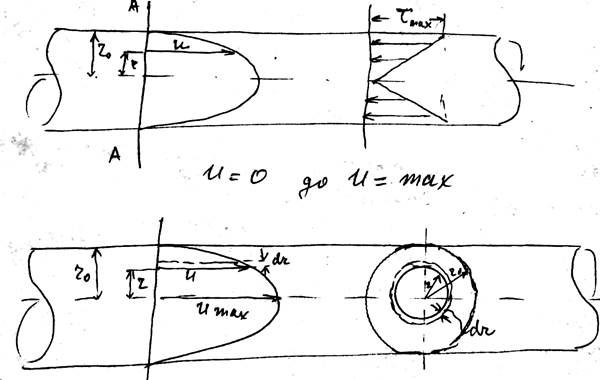
Приравняем уравнения 1 и 2, заменив R = r/2, а первое уравнение представим в виде:

 

τ = - μ du/dy (знак минус указывает на уменьшение скорости в направлении радиуса)

ρ g r/2 Y = τ = - μ du/dy;

 

Полученное уравнение решаем относительно du:

du = - ½ ρ gr Y dr / μ;

Интегрируем полученное выражение:

u = - ½ ∫ (ρ gY / μ ) rdr = - (ρ gYr²/4 μ ) + C

Постоянную интегрирования С найдем принимая r = r₀ a u = 0

C = ρ gY / 4μ r₀², отсюда u = ρ gY / 4μ r₀² - ρ gY / 4μ r²

u = ρ gY / 4μ (r₀² – r²)

 Мы получили закон распределения скорости при ламинарном режиме. При r =0 u = u_max

u_max = (ρ gY / 4μ ) r₀²

Расход и средняя скорость

Расход жидкости в трубе можно найти суммированием элементарных расходов, проходящих через кольцо радиусом r и шириной dr, т. е. из выражения: Q = ∫ ₀^{r 0} u 2 ∏ rdr, подставим значение U

Q = ∫ ₀^r ρ gY / 4μ (r₀² – r²) 2 ∏ rdr = ρ gY∏ / 2μ (r₀² – r²) rdr = ρ gY∏ / 2μ [r₀²∫ ₀^{r 0}rdr - ∫ ₀^{r 0}r³ dr]

r₀²∫ ₀^{r 0}rdr = r₀⁴/2; ∫ ₀^{r 0}r³ dr = r₀⁴/4; r₀⁴/2 - r₀⁴/4 = r₀⁴/4

Q = ρ gY∏ / 8 μ

Средняя скорость определяется деление Q на W = ∏ r₀²

U = Q/W = ρ gYr₀² / 8μ; U = ρ gYr₀² / 8μ

 

Сравним два уравнения:

U = ρ gYr₀² / 8μ и u_max = (ρ gY / 4μ ) r₀², получим U = u_max/2

при ламинарном режиме.

 

Потери напора на трение в круглой трубе при ламинарном движении.

 

Потери напора определим пользуясь уравнением:

U = ρ gYr₀² / 8μ

Решаем его относительно уклона и заменим радиус диаметром, т. е. r₀=d/2

Y =8μ U4 / ρ gd² = 32 μ U / ρ gd²

Умножим левую и правую часть уравнение на длину ℓ:

Yℓ = hℓ 8μ Uℓ / ρ gd² = 32 vℓ U / gd², где v = μ /ρ;

h_ℓ = 32 vℓ U / gd² формула Паузейля-Гагена

Потери напора при ламинарном движении пропорционально скорости.

Преобразуем полученную зависимость домножив и разделив правую часть на 2U

h_ℓ = 32 vℓ U / gd^{2 .} 2U/2U = 64 vℓ U²/ gd d 2U = 64 vℓ U²/Udd2g, где 64v/Ud = 64/R_e = λ

При ламинарном движении коэффициент гидравлического трения, зависящий от числа Рейнольдса.

h_ℓ = λ (ℓ U²/ d 2g) формула Дарси-Вейсбаха.

Мы получили общую зависимость потерь напора, где λ не зависит от шероховатости а только от R_e.

 

Турбулентный режим течения жидкости

 

При переходе числа Рейнольдса через критическое значение движение становиться турбулентным, т. е. начинается интенсивное перемешивание жидкости и частицы жидкости описывают сложные траектории и местные скорости имеют три составляющие.

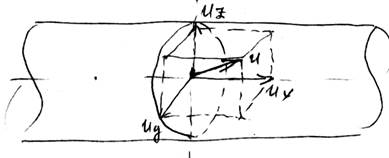Скорость в точке турбулентного потока называют мнговенной линейной скоростью или актуальной.

u_x – продольная составляющая

u_y, u_z – поперечные составляющие, лежащие в сечении.

 

Эти скорости постоянно изменяются. Изменение во времени каждой составляющей называют пульсацией скорости.

 

u_x¹ = u_x - u‾ _x;    ∑ u_x¹dx = 0

 

u‾ _x – определенная скорость, равная высоте прямоугольника АВСD, равновелиного площади, заключенный между пульсационной кривой..

Разность между актуальной и осредненной скоростями называется пульсационной составляющей - u_x¹

Осредненная скорость может быть представлена в виде u‾ _x = 1/Т ∫ ₀^т u_xdt, где Т – период наблюдений. Т. о. можно осреднить u_y и u_z.

Турбулентный поток можно считать установившемся лишь по осредненным скоростям.

В турбулентном потоке происходит непрерывное перемешивание. Интенсивность его не одинакова по сечению трубы. Чем дальше от стенок, тем больше перемешивание. Часть потока занята турбулентным ядром и лишь у стенок образуется тонкий ламинарный слой или пленка.

В пределах ламинарной пленки скорость изменяется от нуля до некого граничного значения u_гр. Далее эпюра скоростей выравнивается.

Толщина ламинарной пленки зависит от диаметра трубы и скорости течения жидкости:

∂ _л = 32, 88 d/R_e√ x

Для одной и той же трубы ∂ _л обратно-пропорциональна средней скорости потока.

 

 

Понятие о гидравлически гладких и шероховатых стенках.

Внутренняя поверхность стенок отличается шероховатостью, зависящий от материала труб, характера отработки и условий эксплуатации.

Шероховатость можно представить в виде бугорков со средней высотой ∆, называемой абсолютной шероховатостью.

Для стальных труб ∆ = 0, 065/0. 1 мм, а для чугунных ∆ = 0, 25 мм

Отношение ∆ к линейному размеру поперечного сечения потока называется относительной шероховатостью, для круглых труб ∆ /r

Отношение линейного размера к абсолютной шероховатости называется относительной гладкостью r/∆

Соотношение абсолютной шероховатости и толщины ламинарной пленки позволит выделить следующие случаи:

1. Гидравлически гладкие трубы: ∂ _л > > ∆

2. Гидравлически шероховатые трубы: ∂ _л  < ∆

3. Некотрый промежуточный случай: ∂ _л  = ∆

 

Касательные напряжения при турбулентности движения жидкости.

В потоке жидкости касательные напряжения представляют сумму τ _лам и τ _труб, т. е. τ = τ _л + τ _т

Рассмотрим два слоя движущейся жидкости с площадью соприкосновения S и относительной скоростью между слоями  u.

Т – сила трения

Количество движения равно импульсу силы трения: mu = T ^. t

m = ρ V, V = ℓ S, т. е. m = ρ ℓ S

 

 

u ρ ℓ S¹ = T ^. t или T = ρ (ℓ /t) Su

ℓ /t = u¹ – скорость поперечного перемещения точки «m»

Т = ρ S¹u¹u

По теории Прандтля   u = ℓ (du/dy); u¹ = ℓ (du/dy), где ℓ - расстояние между слоями, а y – расстояние от стенки трубы.

Т = ρ Sℓ ² (du/dy)², разделив почленно уравнение на площадь S, получим касательные напряжения.

τ _т = Т/S = ρ ℓ ²(du/dy)²

ℓ - длинна пути перемешивания по Прандтлю.

ℓ = χ y, где χ - постоянна Кармана, равная 0, 4 и определяющая толщину слоя.

Шевелев определил χ = 0, 338 / d^{0, 08}

Т. о. τ = + μ (du/dy) + ρ ℓ ² (du/dy)²

При ℓ = 0, τ = μ (du/dy) – режим ламинарный

τ = ρ ℓ ² (du/dy)² – режим турбулентности.

 

 

 

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: