Лекция №5

                                                  Характеристики движения жидкости.

                                                  Уравнение неразрывности потока.

                                                  Уравнение Д. Бернулли для эл. струйки

                                                    идеальной жидкости.

Расход жидкости. Расходом жидкости называется ее объем, проходящий в единицу времени через живые сечения:

 

Q = V/t [L³/t]

 

Единицы измерения: м³/с, см³/с, дм³/с, или л/с.

Если чрез dW обозначить элементарную площадь живого сечения, то величина элементарного расхода будет представлять собой:

 

dQ = udW

 

Т. к. скорости «u» в различных точках сечения неодинаковы, то величину расхода Q можно представить в виде:

 

Q = ∫ _w udW

 

Структурная особенность течения. Скорости течения u в разных точках неодинаковы, вводим понятие средней скорости.

u₁ ≠ u₂ ≠ u₃ и т. д.

Это фиктивная, реально не существующая скорость «U»

Скорость «U» - это отношение расхода жидкости к площади живого сечения потока:

U = Q/W; U = ∫ _w udW / W

Величина расхода Q для данного живого сечения: Q = U ^. W

 

Эпюра скоростей.  Рассмотрим поток, имеющий плоские живые сечения в круглой трубе.

 

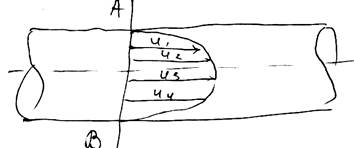Наметим вертикаль АВ. Векторами покажем скорости каждой элементарной струйки u₁ , u₂ , u₃ и т. д. Соединив концы этих векторов плавной линией получим эпюру скоростей. Эпюрой скоростей называют графическое изображение изменения скоростей по живому сечению.   U = S_эп / d

Уравнение неразрывности или сплошности потока.

Для определения далений и скоростей в различных точках потока жидкости используют основные уравнения гидродинамики. Эти уранения получены при наличии связи параметров движения с силами, действующими на движущуюся жидкость.

Уравнение неразрывности потока является аналитическим выражением закона сохранения массы в движущейся жидкости. Поток будет сплошным, если в нем не образовывается разрывов и пустот, т. е. ρ = const.

В дифференциальной форме это уравнение имеет вид:

 

∂ u_x / ∂ _x + ∂ u_y / ∂ _y + ∂ u_z / ∂ _z

 

Мы же будем использовать для расчетов уравнение неразрывности в гидравлической форме.

Рассмотри установившееся движение жидкости в трубе переменного сечения и выберем в потоке два произвольных сечения   I - I и II – II.

 

Рассмотрим объем aвcd, заключенный между ними

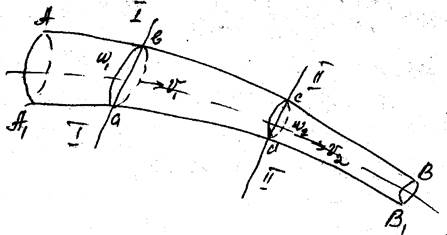
Поток ограничен непроницаемой поверхностью, образованной линией тока. Будем считать, что выбранные сечения неподвижны, а жидкость – протекающая через них.

Обозначим через Q₁ и Q₂ расходы в выбранных сечениях. За время dt через живое сечение с площадью W₁ поступает объем жидкости равный Q₁ dt, в то же время через живое сечение с площадью W₂ вытекает объем Q₂ dt.

Примем следующие допущения:

1. Поверхность АВ непроницаема;

2. Жидкость несжимаема

3. Жидкость движется без разрывов и пустот.

И мы можем утверждать, что объемы равны: Q₁ dt = Q₂ dt или Q₁ = Q₂

Можно в потоке наметить ряд сечений и получить:

 

Q₁ = Q₂ = Q_3…. = Q_n = const, Q = const вдоль потока

 

Это можно представить в следующим виде:

W₁ U₁ = W₂ U₂ = W_n U_n

Это и есть уравнение неразрывности в гидравлическом виде.

 

U₁/ U₂ = W₂ / W₁    Средняя скорость течения жидкости обратно пропорциональны площадям живых сечений потока.

Уравнение Д. Бернулли для элементарной струйки идеальной жидкости при установившимся движении.

Если первым основным уравнениям гидродинамики является уравнение неразрывности, то вторым является уравнение Д. Бернулли, устанавливающее зависимость между скоростью и давлением в различных сечениях одной и той же элементарной струйки.

Движение будем полагать установившимся и плавно изменяющимися. Жидкость идеальной.

 

Пусть за некоторый бесконечно малый промежуток времени dt объем АВ переместится в положение А₁В₁. При этом сечение I – I переместится на расстояние dℓ ₁, а сечение II – II на расстояние dℓ _2.

Для вывода уравнения Д. Бернулли применил к движению объема жидкости АВ теорему об изменении кинетической энергии (теорему живых сил), согласно которой приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на эту систему.

d (KЭ) = ∑ А, где d (KЭ) приращение кинетической энергии тела на некотором расстоянии; ∑ А – сумма работ всех сил, действующих да движущееся тело. KЭ = dm ^. u² / 2

Приращение кинетической энергии будет представлять разность значений кинетической энергии в двух положениях перемещающегося объема, т. е. как разность кинетической энергии А₁В₁ и АВ.

В объемы А₁В₁ и АВ входит как составная часть объем А₁В поэтому может утверждать, что искомое приращение кинетической энергии определяется разностью кинетической энергии объемов ВВ₁ и АА₁.

Определим эти объемы:

АА₁ = dW₁ ^. dℓ ₁ = dW₁ ^. u₁ ^. dt = dQ₁dt

BB₂ = dW₂ ^. dℓ ₂ = dW₂ ^. u₂ ^. dt = dQ₂dt

По условию неразрывности dW₁ ^. u₁ = u₂ ^. dt = dQ = const, следовательно объемы АА₁ и BB₁, равны, т. е.

dQ₁dt = dQ₂dt = dQdt

Масса рассматриваемых объемов равна:

dm = ρ dQdt

Выражение для приращения кинетической энергии примет вид:

d (KЭ) = ρ dQdt ^. U₂² / 2 – ρ dQdt ^. U₁² / 2

Рассмотрим далее работы сил, действующих на объем АВ при перемещении его в положение А₁ В₁

1. Работа силы тяжести. Действие силы тяжести движущегося объема АА₁ проявится при перемещении его в положение ВВ₁. Работа силы тяжести равна произведению этой силы на путь, пройденный точкой ее приложения, т. е. центром тяжести движущегося объема жидкости по вертикали:

А_{с. т.} = ρ dQdt ^. Z₁ - ρ dQdt ^. Z₂

2. Работа сил гидростатического давления.

Работа силы давления определяется силой давления в сечениях на путь, пройденный этими сечениями

∑ А_{с. т.} = P₁ dW₁dℓ ₁ – P₂ dW₂dℓ ₂ = P₁ dW₁u₁dt – P₂ dW₂u₂dt

∑ А_{с. т.} = P₁dQdt – P₂dQdt

Р₁ и Р₂ – гидростатическое давление в сечениях I и II – II

3. Работа сил давления окружающей жидкости на боковую поверхность объема АВ.

Эта работа равна нулю, т. к. эти силы парных u в сумме равны нулю.

4. Работа сил трения. Эта работа равна нулю, поскольку мы рассматриваем идеальную жидкость.

 

Приравняв приращение кинетической энергии объема движущейся жидкости к сумме работ, получим:

 

ρ dQdt ^. U₂² / 2 – ρ dQdt ^. U₁² / 2 = ρ dQdt ^. Z₁ - ρ dQdt ^. Z₂ + P₁ dW₁u₁dt – P₂ dW₂u₂dt

Разделим полученное уравнение почленно на единичную массу dm = ρ dQdt и перегруппируем члены:

gZ₁ + P₁/ρ + u₁²/2 = gZ₂ + P₂/ρ + u₂²/2

Для любого сечения идеальной жидкости:

gZ + P/ρ + u²/2 = const

Это уравнение для элементарной струйки идеальной жидкости Бернулли получил в 1738 г.

Сумма трех слагаемых, входящих в это уравнение называется полной удельной энергией жидкости в сечении и обозначается буквой Е.

gz – удельная энергия положения центра тяжести сечения

Р/ρ – удельная энергия давления в центре тяжести сечения

u² / 2 – удельная кинетическая энергия.

Для элементарной струйки идеальной жидкости полная удельная энергия есть величина постоянная для всех сечений струйки.

С физической точки зрения уравнение Д. Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, отнесенный к единице массового расхода.

gz + Р/ρ – мера потенциальной энергии.

В гидравлике для характеристики удельной энергии пользуются понятием напора, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, т. е. ρ dQdt:

Z₁ + P₁/ρ g + u₁²/2g = Z₂ + P₂/ρ g + u₂²/2g,  или в общем виде

Z + P/ρ g + u²/2g = H = const

 

z – гидравлический напор [м]

Р/ρ g – пьезометрический напор [м]

u² / 2g – скоростной напор [м]       

Сумма трех слагаемых называется гидродинамическим напором Н, а Z + P/ρ g – гидростатический или потенциальный напор.

 

Диаграмма Д. Бернулли

Графическое изображение членов, входящих в уравнение называется диаграммой Д. Бернулли

 

 

 

 

 

 

 

 

 

 

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: