 |
Расположение геометрических объектов в октантах пространства
|
|
|
|
Три взаимно – перпендикулярные плоскости проекций делят пространство на восемь октантов. (рис.5).
Каждый из восьми октантов представляет собой прямоугольный трехгранник, у которого гранями служат части плоскостей проекции, а ребрами – оси координат.
В машиностроении вместо изображения на рис. 5 пространственного макета пользуются эпюром – чертежом, составленным из двух или трех связанных между собой ортогональных проекций геометрического объекта.
При изображении точек геометрических объектов в пространстве и на эпюре используются обозначения [2].
1. обозначения плоскостей проекций:
Н – горизонтальная плоскость проекции;
V – фронтальная плоскость проекции;
W – профильная плоскость проекции;
2. Точки в пространстве обозначаются прописными буквами латинского алфавита.

3. Проекции точек обозначаются строчными буквами:
a – проекция на плоскость H;
a’ - проекция на плоскость V;
a’’ - проекция на плоскость W.
Преобразование пространственного макета в эпюр осуществляется путем совмещения плоскостей W и Н с плоскостью V путем вращения плоскости Н вокруг оси ОХ и плоскости W – вокруг оси ОZ (см.рис.5).
Эпюр точки, расположенной в различных октантах
Положение точки в пространстве определяется тремя координатами (X,Y,Z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций.[3]
Из рис.5 видно, что точка, расположенная в первом октанте, будет иметь положительными все три координаты.
Для построения эпюр точки А, расположенной в первом октанте, необходимо спроецировать точку на плоскости Н, Y, W, совместить плоскости Н и W с плоскостью V, определить значение Qx, Qy и построить a, a’ , a’’ .
|
|
|
При совмещении плоскостей H и W ось у преобразуется в две оси: yH и yW. Ось уН принадлежит плоскости Н, ось yW - плоскости W.[2]
На рис.6,а показан эпюр точки А, расположенной в первом октанте.
Рассматривается построение эпюр точки В, расположенной во втором октанте. Вначале определяется проекция точки на неподвижную плоскость V – в| (рис. 6,б). Проекция точки В на плоскость Н будет располагаться выше оси Х, поскольку плоскость совместится с плоскостью V. Определяется проекция точки на ось уН – вН, затем проекция точки на ось yW - bW. Положение точек b’ и bw определяет проекцию точки b’’ (см.рис.6,б).
На рис. 7 приведены эпюр точек, расположенных в третьем, четвертом, пятом, шестом, седьмом и восьмом октантах.
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ПРЯМЫХ
Понятия и определения.
При ортогональном проецировании на плоскость прямая, не перпендикулярная плоскости проекции, проецируется в прямую.
Для определения проекции прямой достаточно знать проекции двух нетождественных точек, принадлежащих этой прямой.
Прямую, не параллельную ни одной из плоскостей проекций принято называть прямой общего положения. На рис. 8 показана прямая общего положения и ее проекции на три координатные плоскости. На рис. 9 показан эпюр прямой.
Особые положения прямой
Прямая линия может занимать относительно плоскостей проекций особые (или частные) положения:

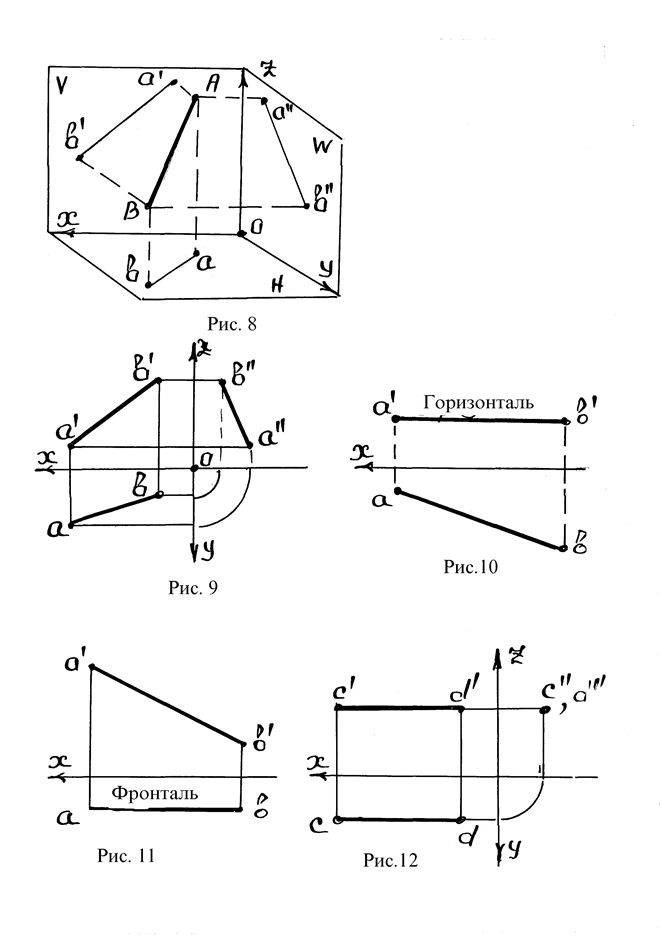
1. Прямая параллельная одной из плоскостей проекций;
2. Прямая параллельная двум плоскостям проекций.
Прямая, параллельная плоскости Н, называется горизонталью (рис.10), плоскости V – фронталью (рис.11).
Следы прямой
Прямая общего положения пересекает все основные плоскости проекций. Точку пересечения (встречи) прямой с плоскостью проекции называют следами прямой. [4,7]
Например, прямая АВ пересекает плоскость V в точке М и плоскость Н – в точке N (рис.13). Оба следа расположены в первом октанте.
|
|
|
Для определения следа пересечения прямой с плоскостью Н следует фронтальную проекцию прямой продлить до пересечения с осью Х (точка n’, рис. 14). В точке пересечения прямой восстановить перпендикуляр к оси ОХ, горизонтальную проекцию прямой продлить до пересечения ее с перпендикуляром.
Аналогично определяется след пересечения прямой с плоскостью V (точка m’, см. рис. 14).
На рис. 15 показана прямая CD, имеющая след пересечения с плоскостью Н во втором октанте. Построение следов прямой с плоскостями проекций показано на рис. 16.
Таким образом, по положению проекций точек М и N можно судить, к каким октантам пространства отнесена данная прямая.
Прямая не имеет следа на плоскости в том случае, когда она параллельна этой плоскости.
Взаимное положение прямых
Параллельные прямые. У параллельных прямых одноименные проекции параллельны (рис. 17).
Пересекающиеся прямые. Если прямые пересекаются, то проекции прямых имеют одну общую точку (точка К, рис. 18).
Скрещивающиеся прямые. На проекциях прямых общая точка отсутствует (рис. 19).
|
|
|


