 |
Прямая, перпендикулярная плоскости
|
|
|
|
Правило: Если прямая перпендикулярна к плоскости, то:
1. Она перпендикулярна к любой прямой, расположенной в плоскости;
2. Горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу плоскости, фронтальная проекция прямой перпендикулярна к фронтальному следу плоскости (рис. 41). [3, 6]
Пример 1. Заданы проекции треугольника АВС. Требуется в точке А восстановить перпендикуляр к плоскости АВС.
Решение: Через точку А проводится горизонталь и фронталь.
На горизонтальной проекции восстанавливается перпендикуляр к горизонтали, на фронтальной проекции – к фронтали.
На перпендикуляре располагают (произвольно) точку D, ограничивающую его длину.
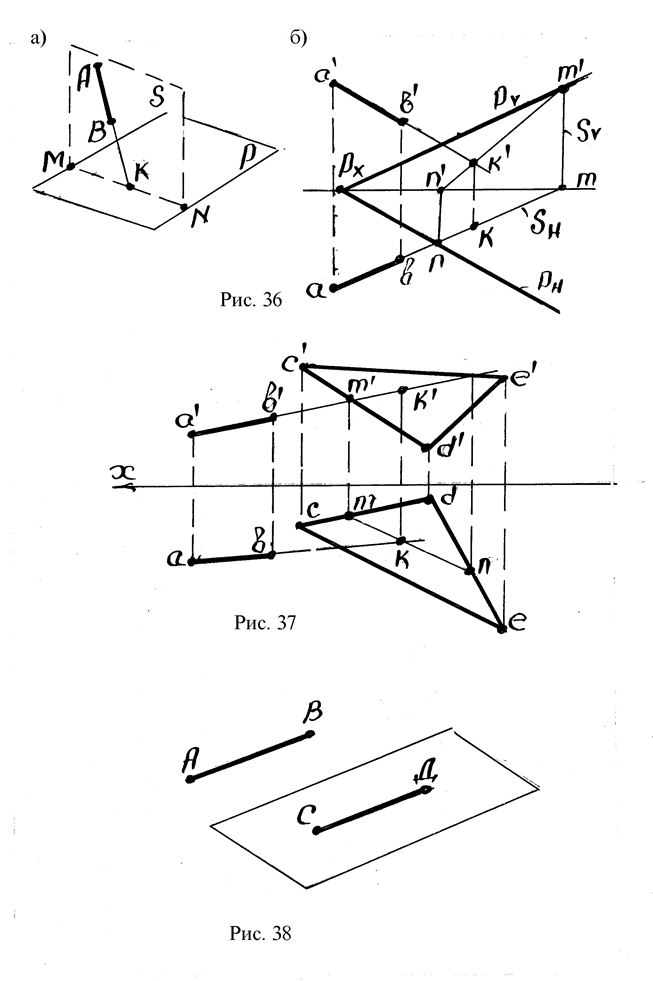

По построению проекция прямой AD (a’d’) перпендикулярна проекции a’m’. Поскольку прямая АМ параллельна плоскости V, то прямые AD и АМ составляют угол 90° (см. правило проектирования прямого угла).
Очевидно прямые AD и AN также составляют угол 90°.
Итак, прямая AD перпендикулярна прямым АМ и AN, расположенных в плоскости треугольника АВС. Следовательно эта прямая перпендикулярна плоскости треугольника АВС.
Пример 2. Задана точка D и проекции треугольника АВС. Требуется определить расстояние от точки D до плоскости треугольника АВС.
Решение: Из точки D опускается перпендикуляр на плоскость треугольника АВС. Для построения проекций перпендикуляра используются горизонталь и фронталь треугольника АВС (АМ, AN, рис. 43).
Определяется точка встречи перпендикуляра с плоскостью треугольника АВС. С этой целью через фронтальную проекцию перпендикуляра проводится вспомогательная фронтально-проектирующая плоскость Q. Эта плоскость пересекает стороны треугольника АВС в точках 1, 2 (см. рис. 43).
|
|
|
На горизонтальной проекции определяется точка пересечения перпендикуляра с линией 1-2 (точка k, см. рис. 43).
Определяется натуральная величина отрезка DК, которая представляет расстояние от точки D до плоскости треугольника АВС.
Угол между прямой и плоскостью
Угол между прямой и плоскостью называется острый угол, образованный этой прямой и ее проекцией на данную плоскость (рис.44,а).
Пример 1. Заданы проекции прямой АВ и следы плоскости Р. Требуется определить угол между прямой и плоскостью (рис.44,б).
Решение: Определяется точка пересечения прямой АВ с плоскостью Р: через проекцию ab проводится горизонтально – проектирующая плоскость Q и находится линия пересечения плоскостей Р и Q (линия МN, см.рис. 44,б). Затем определяется точка пересечения линий МN и АВ – точка D.
Из точки А опускается перпендикуляр на плоскость Р. С помощью вспомогательной горизонтально – проектирующей плоскости находится точка пересечения перпендикуляра с линией пересечения плоскостей S и Р (точка С, см.рис.44,б). На горизонтальной и фронтальной проекциях через точки D и С проводятся прямые.
В результате построения получают проекции угол АВС.
Пример 2. Заданы проекции прямой ВС и точки А. Требуется определить расстояние от точки А до прямой ВС (рис.45,а).
Решение: Через точку А проводится вспомогательная плоскость Р, перпендикулярная прямой ВС: через точку a’ проводится фронталь a’n’ перпендикулярная b’c’; через точку n фронтали проводится след Рн перпендикулярно bc, определяется точка Рх и проводится след Рv параллельно фронтали.
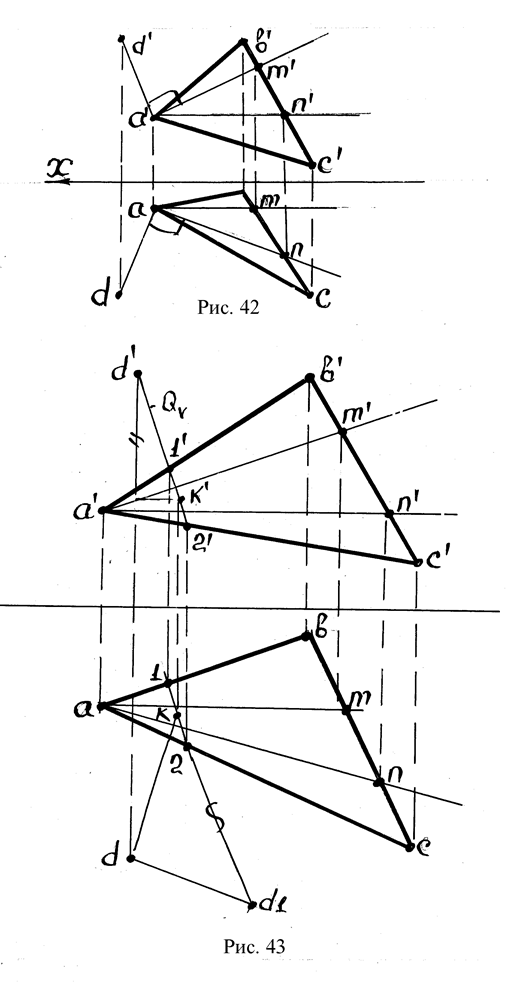

Определяется точка пересечения прямой ВС с плоскостью Р с помощью горизонтально – проектирующей плоскостью Q (точка D, см.рис.45). Определяется натуральная величина отрезка DА, которая представляет расстояние от точки А до прямой ВС.
Параллельные плоскости
Правило: У параллельных плоскостей одноименные следы параллельны между собой (рис.46,а).
|
|
|
Пример. Задана плоскость Р следами и проекции точки К. Требуется через точку К провести плоскость Q, параллельную плоскости Р.[2,7].
Решение: Через горизонтальную проекцию точки К проводится линия, параллельная следу Рн.
Через точку k ’ проводится линия, параллельная оси ОХ до пересечения с перпендикуляром, восстановленным в точке t (рис.46,б).
Через точку t’ проводится след Qv.
Через точку Qх проводится след Qн параллельно следу Рн.
Плоскость Q параллельна плоскости Р, поскольку по построению следы плоскостей параллельны. Плоскость Q проходит через точку k, т.к. эта точка располагается на горизонтали плоскости.
|
|
|


