 |
Перпендикулярные плоскости
|
|
|
|
Правило1: Плоскость (Q рис.47), проведенная через прямую (АВ), перпендикулярную второй плоскости (Р) – перпендикулярна этой плоскости.
Правило2: Плоскость (Q рис.48), перпендикулярная прямой (АВ), расположенной в другой плоскости (Р), перпендикулярна этой плоскости. [6,7].
Пример. Заданы следы плоскости Р и проекции прямой АВ. Требуется через прямую АВ провести плоскость Q, перпендикулярную плоскости Р (рис.49).
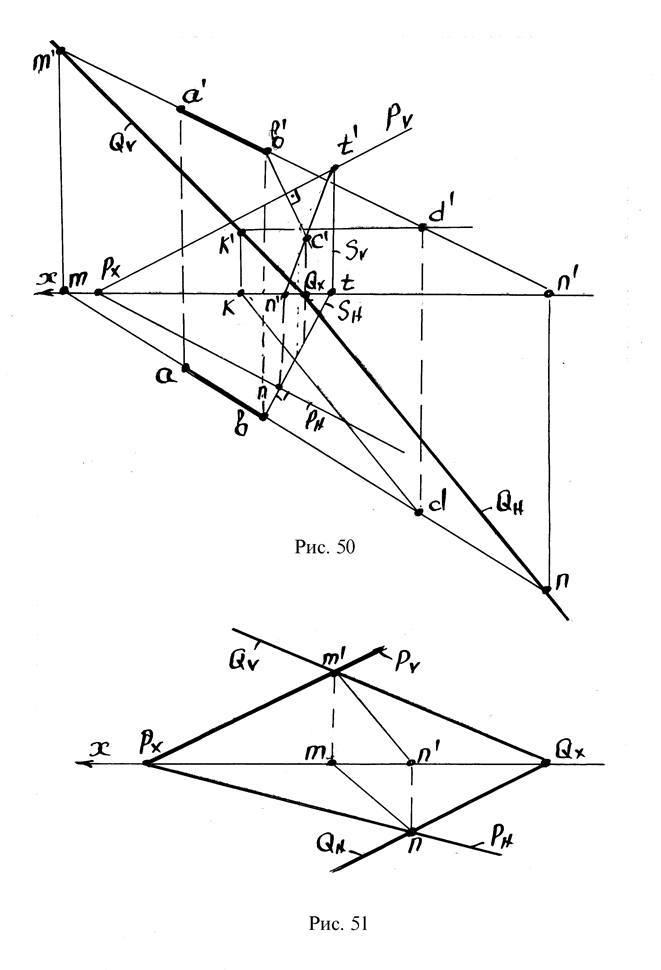
Решение: Из точки В опускается перпендикуляр на плоскость Р и определяется точка пересечения перпендикуляра с плоскостью Р (точка С, рис.50).
Через прямую АВ и точку С проводится плоскость Q: находятся точки пересечения прямой АВ с плоскостями проекции (точки M, N, см.рис.50). Для построения следов плоскости Q используется горизонталь СD, проведенная через точку С до пересечения с прямой АВ (точка D).
Пересечение плоскостей
5.7.1. Прямая линия, получаемая при пересечении плоскостей, определяется двумя точками, из которых каждая принадлежит обеим плоскостям.
Пересечение плоскостей, заданных следами для определения линии пересечения плоскостей используются точки пересечения одноименных следов плоскостей (точки M, N, рис.51).

5.7.2. Пересечение плоскостей, одна из которых задана следами, другая – параллельными линиями.
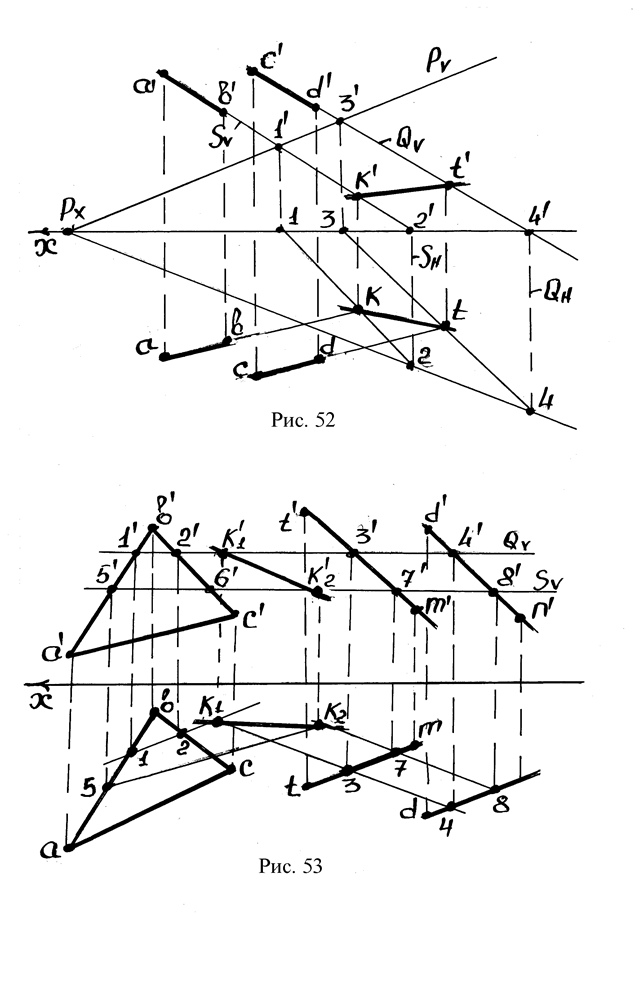
Пример. Плоскость Р задана следами, плоскость R – двумя параллельными линиями АВ и СD. Требуется построить линию пересечения плоскости (рис.52).
Решение: Через фронтальную проекцию прямой АВ проводится фронтально – проектирующая плоскость S и определяется линия пересечения плоскостей S и Р (линия 1-2, см.рис.52). Определяется точка встречи прямой АВ с плоскостью Р – точка К.
Через проекцию c’d’ проводится фронтально – проектирующая плоскость Q и определяется линия пересечения плоскостей Р и Q (линия 3-4, см.рис.52).
|
|
|
Находится точка пересечения линии СD c плоскостью Р (точка Т).
На обоих проекциях через точки К и Т проводятся прямые.
Линия КТ есть линия пересечения плоскостей Р и R.
5.7.3. Пересечение плоскостей, одна из которых задана плоской фигурой (например: треугольником), другая – двумя параллельными линиями.
Пример. Плоскость Р задана проекциями треугольника АВС, плоскость R- двумя параллельными ТМ и DN (рис.53). Требуется построить линию пересечения плоскостей Р и R.
Решение: Проводится вспомогательная фронтально – проектирующая плоскость Q так, чтобы след Qv пересекал фигуру АВС и линии ТМ, DN. Эта плоскость пересекает фигуру АВС в точках 1,2, линию ТМ – в точке 3, линию DN – в точке 4. Строятся горизонтальные проекции точек 1,2,3,4.
На горизонтальной проекции точки 1,2 и 3,4 соединяются прямыми. Находится точка пересечения линий 1-2 и 3-4 (точка К1, см.рис.53).
Проводится горизонтально - проектирующая плоскость S. Эта плоскость пересекает фигуру АВС в точках 5,6, линию ТМ – в точке 7, линию DN – в точке 8.Находятся горизонтальные проекции точек.
Определяется точка пересечения линий 5-6 и 7-8 – точка К2.
Линия К1 К2 есть линия пересечения плоскостей Р и R.
5.7.4. Пересечение плоскостей, заданных тремя точками.
Пример1. Заданы проекции треугольников АВС и MNR. Требуется построить линию пересечения фигур и определить видимую (и невидимую) часть фигур (рис.54).
Решение: Через прямую m’n’ проводится фронтально – проектирующая плоскость Qv. Эта плоскость пересекает фигуру АВС в точках 1’, 2’. Находятся горизонтальные проекции точек и проводится линия 1-2. Определяется точка пересечения линий 1-2 и mn (точка t, см.рис.54).
Через прямую b’ c’ проводится фронтально – проектирующая плоскость Sv. Эта плоскость пересекает фигуру MNR в точках 3’, 4’. Определяются горизонтальные проекции точек и проводится линия 3-4. Находится точка пересечения линий bc и 3-4 (точка d, см.рис.54).
|
|
|

Через точки t и d (а также t’ и d’) проводится линия, которая и является линией пересечения фигур АВС и MNR.
Для определения видимой и невидимой частей фигур проводится анализ взаимного расположения сторон фигур на фронтальной и горизонтальной проекциях.
На фронтальной проекции исследуется взаимное расположение сторон фигур. Например, сторона a’c’ и m’n’ фигур представляет скрещивающиеся прямые.
В точке пересечения фронтальных проекций прямых располагаются две точки. Одну из них располагают на прямой a’c’ (точка 1’, см. рис. 54), другую – на прямой m’n’. Определяются горизонтальные проекции точек.
Из рис. 54 видно, что точка 5, принадлежащая прямой mn расположена дальше от плоскости V, нежели точка 1. Следовательно, на фронтальной проекции прямая m’n’ будет видимой, а прямая a’c’ – невидимой в зоне фигуры m’n’k’.
Аналогично исследуется горизонтальная проекция фигур. Например, в точке пересечения прямых nk и ab располагаются две точки: точка 8 – на прямой ab, точка 9 – на прямой nk. Определяются фронтальные проекции точек и по их расположению определяется видимая часть одной из фигур.
В рассматриваемом примере точка 9, принадлежащая прямой n’k’ расположена выше точки 8 относительно плоскости Н. Следовательно, на горизонтальной проекции прямая ab будет невидимой в зоне фигуры mnk.
Пример 2. Заданы проекции треугольника BCD. Требуется построить проекции треугольника BNK, перпендикулярного стороне CD, найти линию пересечения треугольников BCD и BNK, а также определить «видимость» фигур.
Решение: На фронтальной проекции проводится прямая b’n’ перпендикулярно прямой d’c’. Длина отрезка b’n’ выбирается произвольно (рис. 55).
На горизонтальной проекции проводится линия bn параллельно оси Х.
Через точку b проводится линия bk перпендикулярно прямой dc (длина отрезка bk – произвольна). Строится фронтальная проекция прямой b’k’.
На обеих проекциях точки B, N, K соединяются прямыми. В результате построения получают проекции треугольника BNK (см. рис. 55).
Определяется линия пересечения треугольников BCD и BNK. Через прямую nk проводится горизонтально- проектирующая плоскость S. Эта плоскость пересекает стороны треугольника BCD в точках 1, 2.
|
|
|
На фронтальной проекции определяется точка пересечения прямых c’d’ и 1’-2’ (точка m’- см. рис. 55).
Прямая ВМ есть линия пересечения треугольников BCD и BNK.
5.7.5. Определение «видимости» фигур.
На фронтальной проекции исследуется взаимное расположение прямых b’n’ и c’d’. На прямой c’d’ располагается точка 3’, на прямой b’n’ – точка 4’.
Исследуется расположение точек на горизонтальной проекции. Очевидно, прямая cd располагается дальше от плоскости V, нежели прямая bn.
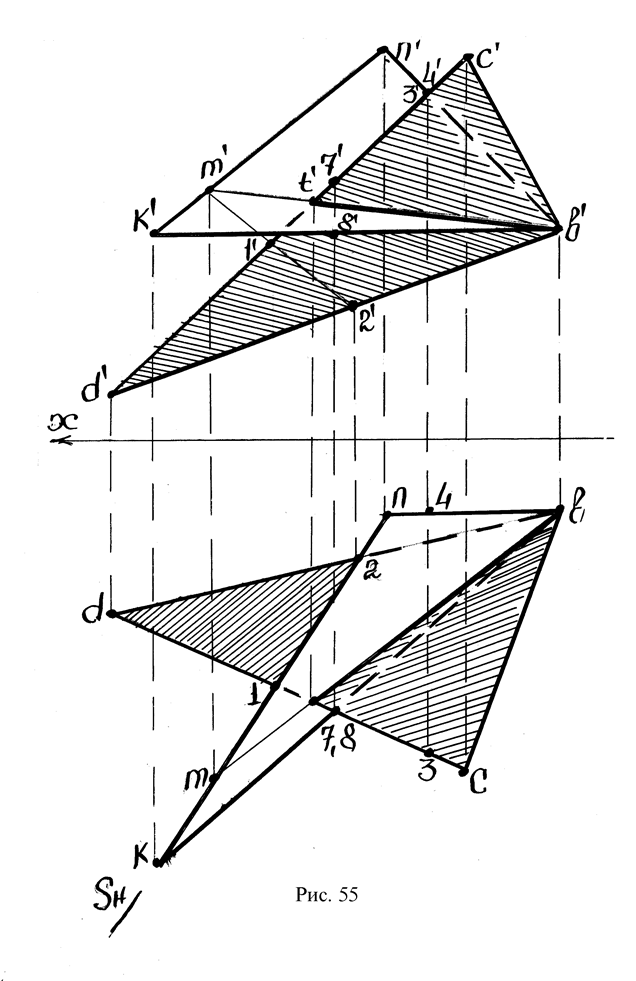
Следовательно, на фронтальной проекции прямая b’n’ будет невидимой в зоне треугольника BCD.
Исследуется взаимное расположение прямых bk и dc. На прямой bc располагается точка 7, на прямой bk – точка 8. По расположению фронтальных проекций точек 7’, 8’ делается заключение: прямая dc будет невидимой в зоне треугольника BNK (на горизонтальной проекции).
|
|
|


