 |
1.3. Порядок виконання роботи. 1.4. Зміст розрахункової роботи
|
|
|
|
1. 3. Порядок виконання роботи
1. Статична сторона задачі.
Звільняємося від в’язів і заміняємо їх реакціями. Проводимо переріз в заданих стержнях і направляємо зусилля у бік розтягу. Визначаємо кількість невідомих і ступінь статичної невизначності системи. Для заданої статично невизначної системи вибираємо таке рівняння статики, яке не містить реакцій опори, тому що останні за умовою задачі визначати не потрібно.
2. Геометрична сторона задачі.
Складаємо план переміщень. Користуючись геометричними умовами, знаходимо залежності між деформаціями стержнів. При цьому звертаємо увагу на умову сумісності деформацій. тобто відповідність знаків зусиль і деформацій.
3. Фізична сторона задачі.
Виражаємо деформації стержнів через відповідні зусилля за законом Гука.
4. Синтез.
Вирішуючи сумісно рівняння статики та рівняння деформацій, визначаємо зусилля в стержнях.
5. З умови міцності при розтязі (стиску) визначаємо площі перерізу стержнів.
1. 4. Зміст розрахункової роботи
Абсолютно жорсткий невагомий брус підтримується однією опорою і двома стержнями: сталевим - 1 та мідним - 2. Стержні зазнають силового навантаження та впливу температури і монтажа.
Для заданої стержневої системи потрібно:
1. Визначити зусилля в стержнях від заданого навантаження P та q, розмір а, довжини стержнів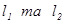 
, співвідношення площ F1: F2 задані;
2. Обчислити напруження при зміні температури в стержнях на величину DТ1 та DТ2;
3. Обчислити монтажні напруження в стержнях, якщо їх фактичні довжини відрізняються від проектних розмірів на величини d1 і d2;
4. Визначити площі перерізу стержнів з урахуванням невигідного сполучення навантажень.
|
|
|
При розрахунках у всіх варіантах завдань прийняти такі характеристики матеріалів:
- модулі пружності, Е1 = 2· 105 МПа, Е2 = 1· 105 МПа;
- розрахункові опори, R1=210 МПа, R2 = 120 МПа;
- коефіцієнти лінійного розширення: a1 = 1, 25·10-5 град-1, a2 = 1, 65·10-5 град-1.
Приклад виконання розрахункової роботи
Р = 660 кН, q = 280 кН/м, а = 1 м, 
, b1 = 0, а = 1 м,
 |
b2=300, F1: F2 = 0, 25; DT1 =300, DT2= - 100, d1 = -0, 1 см, d =0, 05 см.
Рис. 1. 2
1. Визначаємо ступінь статичної невизначності системи:
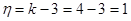
Таким чином потрібно скласти одне додатке рівняння.
2. Визначаємо зусилля в стержнях від заданих навантажень.
а) Статична сторона задачі.
На рис. 1. 3 показані невідомі зусилля N1 і N2, які направлені у бік розтягу та реакції RС і НС.
Складаємо рівняння рівноваги системи сил, що діють на абсолютно жорсткий брус АВ:
å mc = 0: P·а - q · 2a · а - N1 · 2а + N2 · 3а · cos b2 = 0
або N1 - 1, 3 N2 = 50 (кН) (1. 5)
 |
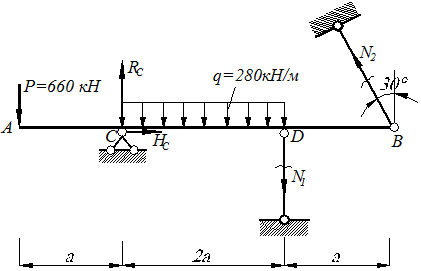Рис. 1. 3
в) Геометрична сторона задачі
Під дією навантаження брус АВ повертається відносно опори С. З урахуванням малісті деформацій переміщення точок бруса по дузі заміняємо переміщеннями по хорді. Система після деформації має вигляд, показаний на рис. 1. 4.
 |
Рис. 1. 4.
Трикутники СВВ1 і CDD1 подібні
або Dl1 cos 300 + 2Dl2 (1. 6)
Приводимо у відповідність деформації стиску. Для цього перед Dl2 потрібно поставити знак “ - ”.
с) Фізична сторона задачі
Після підстановки замість деформацій їх значень згідно до закону Гука (1. 3) у рівняння (1. 6), одержуємо:
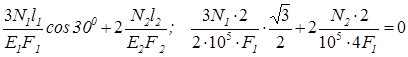
або після спрощення N1 + 0, 385N2 = 0 (1. 7)
d) Синтез
Вирішуємо рівняння (1. 5) і (1. 7)
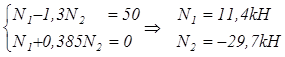
3. Визначаємо температурні напруження в стержнях: при Р = 0, q=0, dі=0, DТ1 = 300С, DТ2 = - 100С.
а) Статична сторона задачі
|
|
|
Рівняння рівноваги у цьому випадку записуємо без урахування навантажень у вигляді
Представимо це рівняння в напруженнях:
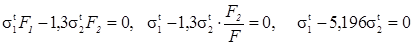(1. 8)
b) Геометрична сторона задачі
Додаткове рівняння (1. 6) повинно містити деформації, що обумовлені перепадом температур.
3Dl1С cos 300 + 2Dl2С =0
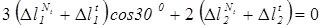
c) Фізична сторона задачі
Запишемо це рівняння в напруженнях
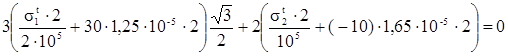
Після спрощення одержуємо:
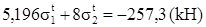(1. 9)
d) Синтез
Вирішуємо спільно рівняння (1. 8) і (1. 9):
Обидва стержні від температурного впливу стиснуті.
4. Визначаємо монтажні напруження: при Р = 0, q=0, Dti = 0,
d1 = - 1· 10-3м, d2= 5· 10-4м.
а) Статична сторона задачі
Активне навантаження у цьому випадку теж відсутне, тому рівняння рівноваги в напруженнях матиме вигляд згідно (1. 5):
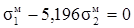(1. 10)
b) Геометрична сторона задачі
Додаткове рівняння в цьому випадку повинно містити деформації з урахуванням відхилень фактичних розмірів довжин стержнів від проектних.
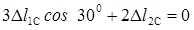
c) Фізична сторона задачі
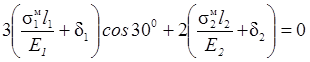
Після спрощення одержуємо:
(1. 11)
d) Синтез
Вирішуємо спільно рівняння (1. 10) та (1. 11)
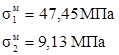
Таким чином задані в умовах задачі відхилення фактичних розмірів стержнів від їх проектних величин викликають додаткові розтягуючі напруження.
5. Визначаємо площі перерізу стержнів з урахуванням невигідних комбінацій навантажень. При цьому припускаємо, що навантаження Р и q діють постійно, а температурні і монтажні впливи можуть бути, або не бути. Сумарні напруження не повинні перевищувати відповідних розрахункових опорів не більш, ніж на 5%.
Результати розрахунку по визначенню напружень від силових, температурних та монтажних впливів наведено у таблиці 1. 1.
Таблиця 1. 1
| Напружен- ня в стержнях | Постійне наванта- ження N (кН) | Тимчасове діяння, МПа | Fi, (см2) до корек- ції | Fi, (см2) після корекції |
sіфакт. (МПа) | |
| темпера-тура | монтаж | |||||
| s1 | 11, 4 | -38, 3 | 47, 45 | 0, 7 | 0, 7 | |
| s2 | -29, 7 | -7, 4 | 9, 1 | 2, 65 | 2, 8 | -113, 5 |
Умова міцності для першого стержня при невігідному навантаженні:
|
|
|
м2 = 0, 7 см2.
Для другого стержня
м2 = 2, 64 см2
Отримане співвідношення площ:
відрізняється від заданого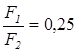 
.
Отже, із умови 4F1 = F2, одержимо:
1 рішення
2 рішення.
Умові задачі задовольняє 1 рішення, тому що
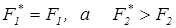
Визначаємо фактичні напруження в стержнях з урахуванням прийнятих значень площ:
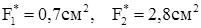
МПа = R1
|
|
|
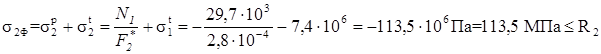
