 |
I ділянка 0 £ z1 £ 3
|
|
|
|
I ділянка 0 £ z1 £ 3
Qy = - q× 2+P+q× z1 = 1+ q× z1, Q(0) =1кН; Q(3)= 7 кН
Mx = q × 2 (2 + z1) – P × (1 + z1) + M - (qz2) / 2 = 10 - z1 -  ;
;
M(0) = 10 кНм; M(3) = -2 кНм;
Епюра Qy на першій ділянці знакопостійна, тому епюра Мх не має екстремума.
II ділянка 0 £ z2 £ 1
Qу=P - q · 2 = 5 - 4 = 1 кН;
Mx = - P · z2 + q · 2 (1 + z2) = 4 - z2;
M(0) = 4 кНм; M(1) = 3 кНм
III ділянка 0 £ z3 £ 2
Qy =- qz3 = -2z3; Q(0) =0; Q(2)= -4 кH;
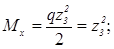 M(0)=0; M(2)=4кНм;
M(0)=0; M(2)=4кНм;
 ; z3 = 0
; z3 = 0 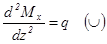
5. По знайденим значенням будуємо епюри (рис. 3. 5 б, в).
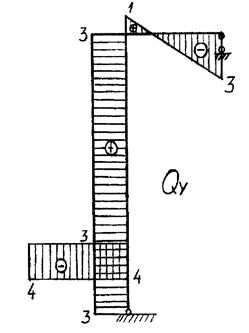
6. На епюрі Мх стрибок у точці В відповідає зосередженому моменту М=7кНм. На епюрі Qу маємо стрибок у точці С на величину сили Р=5кН. На першій і другій ділянках епюра Q додатня (Qy > 0), тому функція моменту зростає. На третій ділянці Qy< 0 функція моменту зменшується від 4 кН до 0.
7. Підбираємо поперечні перерізи балок, виходячи з умови міцності по нормальним напруженням при згині (3. 3). Знаходимо потрібний момент опору на згин

Для балки Mmax=10кНм.

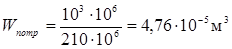 =47, 6 см3
=47, 6 см3
а) приймаємо переріз з двотавра № 12, Wx=58, 4 см3, F=14, 7см2

в) приймаємо переріз із двох швелерів. Для одного швелера  см3
см3
Приймаємо 2 [ № 8 Wx=22, 4· 2=44, 8см3
F = 2· 8, 98 = 17, 96 см2;
с) прямокутний переріз (h=2b)

Wx = Wпотр;  см;
см;
h = 2b - 2 · 4, 15 = 8, 3 см;
F = 8, 3 · 4, 15 = 34, 4 см2;

d) круглий переріз
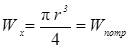
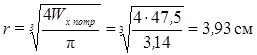 ;
;
F = pr2 = 3, 14 · 3, 932 = 49, 2 см2
f) порівнюємо балки з різними поперечними перерізами по масі на 1 погонний метр довжини.
G1пм=V· g = F · l· g, l·g - const
де g - вага матеріалу об’ємом 1 м3.
Отже, достатньо порівняти балки по площі поперечного перерізу.
Результати розрахунку зводимо в табл. 3. 1
Таблиця 3. 1
| № п/п | Тип перерізу | Розмір | F, см2 | % |
| Iдвотавр | I № 12 | 14, 7 | 100 | |
| 2 | ] [ швелер | [ № 8 | 18 | 122 |
| h=8, 3см b=4, 15см | 34, 4 | 234 | ||
 4 4
| r = 4см | 49, 2 | 334 |
|
|
|
Найбільше раціональною є двотаврова балка.
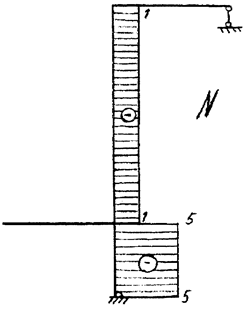
Приклад 4. Для рами, зображеної на рис. 3. 6 а, побудувати епюри М, Q, N.
1. Перевіряємо статичну визначність рами.
Задана рама є статично визначною, тому що для знаходження трьох опорних реакцій RA, HA і RЕ маємо три рівняння статики.
2. Визначаємо опорні реакції рами:
å Z = 0; - HA+ P1 = 0; HA = P1 = 3 кН;
å МА = 0; P2 · 2 + M - P1 · 4 - q · 2 · 1 + RE · 2 = 0;
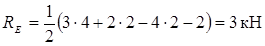
å МЕ = 0; НА · 4 - М - Р2 · 4 - q · 2 · 1 + RA · 2 = 0;

Перевірка:
å Fу = RA - q · 2 - P2 + RE = 5 - 4 - 4 + 3 = 0.
3. Визначаємо кількість ділянок: Межами ділянок у рамах, крім перелічених для балок, є вузли рами. Ця рама має 4 ділянки.
4. Записуючи вирази М, Q, N для стояків рами, треба умовно стати обличчям до цього елемента з будь-якої сторони і діяти як у випадку з балкою. Враховуючи, що момент Мх при підході з різних сторін має протилежні знаки, останні на епюрі Мх не зазначаються. Ординати епюр відкладаються перпендикулярно до осі рами.
I ділянка 0 £ z1 £ 2;
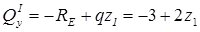 ;
;  ;
; 
 ;
; 
 ;
;

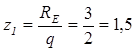 м;
м;
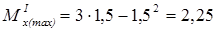 кНм.
кНм.
 (Ç ) - опукла
(Ç ) - опукла
II ділянка 0 £ z2 £ 3;
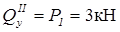 ;
; 
 ;
;  -7кНм
-7кНм
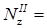 - q · 2 + 2 = -2 кН.
- q · 2 + 2 = -2 кН.
III ділянка 0£ z3£ 2
Qy = - P = - 4 кН
Mx = - P · z3 = -4 z3; 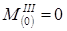 ;
; 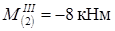

IV ділянка 0 £ z4 £ 1;
Qy = НА = 3 кН;
 M(0) =0; M(1)= 3 кНм.
M(0) =0; M(1)= 3 кНм.
 - RA = - 5 кН.
- RA = - 5 кН.
5. По знайденим значенням будуємо епюри М, Q, N (рис. 3. 6).
6. З метою контролю правильності побудовання епюр перевіряємо рівновагу усіх вузлів.
При цьому повинні виконуватися умови:
å х = 0; å у =0; å Мi =0.
У перерізах, розташованих нескінченно близько до вузла, прикладаємо внутрішні силові фактори М, Q, N відповідно до прийнятого правила знаків. Для вузла, що розглядається необхідно також прикласти зосереджені навантаження Мi та Pi.
|
|
|
Згинаючий момент, діючий у перерізі рами, направляємо від ординати під стержень, рис. 3. 7.
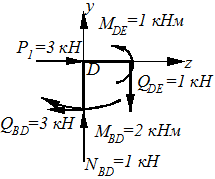
Вузол D
å MD = MDE - MBD = 2 - 2 = 0;
å Fу = - QDE + NBD = -1+1=0;
å Fz = QBD + P = -3+3=0.
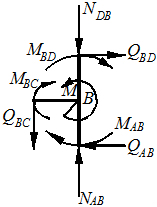

Вузол В
å MD = MBD + MAB - M - MBC = 7+3-2-8=0
å Fу = - QBC + NAB - NDB = - 4 + 5 - 1 = 5-5 = 0;
å Fz = QBD - QAB = 3-3=0.
Вузли рами знаходяться в рівновазі.
Рис. 3. 7

 |
 |
| |||
 | |||
|
Рис. 3. 6
РОЗРАХУНКОВО-ПРОЕКТУВАЛЬНА РОБОТА 4
Розрахунок на міцність та жорсткість балки при плоскому згині
4. 1. Питання до самостійної роботи
1. У чому полягає повна перевірка міцності балки?
2. Для яких поперечних перерізів по довжині балки проводяться визначення smax та tmax?
3. У яких точках по висоті перерізу балки діють smax і tmax?
4. Назвіть основні правила визначення переміщень за методом початкових параметрів.
5. Як визначити напрямок переміщень за методом початкових параметрів?
6. Назвіть порядок визначення переміщень з використанням способу Верещагіна.
7. Який зміст вкладається в термін “перемноження епюр” за способом Верещагіна?
8. На які прості фігури розподіляються вантажні епюри? Де знаходяться центри ваги цих фігур?
9. Як визначається напрямок за способом Верещагіна?
10. У чому полягає розрахунок балки на жорсткість?
|
|
|


