4.2. Стислі теоретичні зведення

Повна перевірка міцності балки полягає в обчислюванні s_max та t_max і розрахункових напружень у небезпечних точках перерізу згідно за III або IV теорії міцності.

Максимальні нормальні напруження s_max діють у перерізі балки, де виникає максимальний згинаючий момент М_max відповідної епюри, і з’являються у точках перерізу балки у найбільш віддалених від нейтральної осі х. Величина цих напружень за умовою міцності не повинна перевищувати значення розрахункового опору R матеріала балки:

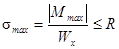                                 ,                                                   (4. 1)

W_x - момент опору поперечного перерізу балки на згин.

Максимальні дотичні напруження t_max, діють у перерізі балки, що співпадає з максимальною ординатою поперечних сил Q_max і виникають в точках, що лежать на нейтральній осі х.

Умова міцності за дотичними напруженнями має такий вигляд:

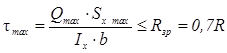                                                         (4. 2)

 - статичний момент половини площі поперечного перерізу балки відносно нейтральної осі х;

I_х - момент інерції поперечного перерізу балки відносно нейтральної осі х;

b - ширина перерізу балки в тій точці по її висоті, де визначається t_мах;

R_зр – розрахунковий опір матеріалу балки на зріз.

 

Перевірка міцності за III або IV теоріями міцності проводиться для конкретного перерізу “mn” по довжині балки, де діють достатньо великі згинаючий момент M_mn і поперечна сила Q_mn. Ідеальний випадок, коли в перерізі балки діють M_max і Q_max. Для балки, що виконана з двотавра, небезпечною є точка 2, яка знаходиться у стінці під полицею. В ній нормальні напруження

                          ,                                              (4. 3)

де 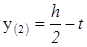                                                                                         (4. 4)

дотичні напруження

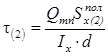                                                                             (4. 5)

де статичний момент полиці відносно нейтральної осі х

                                                                   (4. 6)

Умови міцності згідно з третьою та четвертою теоріями, відповідно, мають вигляд:

                                                             (4. 7)

                                                             (4. 8)

Епюри s і t для І показані на рис. 4. 1.

 

Рис. 4. 1

 

У випадку, якщо розрахункове напруження s_р згідно однієї з теорій міцності виявиться більше розрахункового напруження R, необхідно перейти до двотавру наступного номера і виконати для нього повну перевірку міцності, як вказано вище. Крім розрахунків на міцність виконуються розрахунки на жорсткість. З цієї метою в балках визначаються прогини, наприклад, методом початкових параметрів.

 

4. 2. 2. Рівняння для визначення переміщень у поточних точках по довжині балки за методом початкових параметрів має такий вигляд (рис. 4. 2).

Рис. 4. 2.

 

(4. 9)

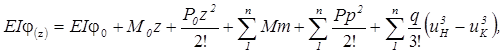     (4. 10)

де v₍z₎, j_(Z) - прогин і кут повороту в перерізі балки, що розташований на відстані z від початку координат;

v ₀, j₀ - прогин та кут повороту на початку координат;

М₀, P₀ - зовнішній момент та зосереджена сила на початку координат;

Р, М, q - навантаження на балку; на рис. 4. 2 показано їх позитивні напрямки;

m, p - відповідні відстані від розрахункового перерізу mn до моменту і сили,

тобто                     p = z - a_p, .                    m = z - a_m.

u_н, u_к - відстань від розрахункового перерізу mn до початку та кінця дії розподіленого навантаження, тобто

        u_н = z – a_н                      u_k = z –a_k

Правила користування рівняннями (4. 9), (4. 10)

Початок координат вибираємо в крайній точці ліворуч або крайній точці праворуч балки.

Знаки додатків, що входять у рівняння, визначаємо за правилом знаків згинаючих моментів.

В рівнянні враховують навантаження, що розташовані між початком координат та розрахунковим перерізом mn.

Правило знаків при визначенні переміщень:

- прогин спрямований у позитивному напрямку осі у;

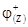- поперечний переріз повертається проти годинникової стрілки (ось z праворуч), поперечний переріз повертається за годинниковою стрілкою (ось z ліворуч).

Початкові параметри v₀ і j₀ визначаються з кінематичних умов (закріплення балки на опорах), М₀ та P₀ із умов рівноваги (реакції в опорних точках балки рис. 4. 3, рис. 4. 4, рис. 4. 5).

 

 

при z = 0, vА = 0;

при z = l vв = 0

 

 

               Рис. 4. 3

 

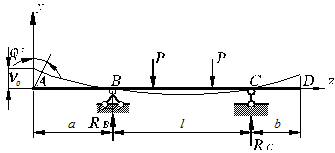
початок координат т. А

 

                    Рис. 4. 4

 

 

при z = 0

vА= 0, jА = 0

M0 = - MА, P0 = RА

 

                      Рис. 4. 5

 

Формула Верещагіна:

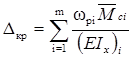                                                                       (4. 11)

де m - кількість простих фігур, визначається одиничною епюрою;

складові частини площі епюри згинаючих моментів вантажного стану за номером i;

 - ординати одиничної епюри згинаючих моментів під центрами ваги складових частин епюри моментів вантажного стану.

 

Порядок визначення переміщень згідно способу Верещагіна

 

Щоб скористатися формулою (4. 11) для визначення переміщення розглядається два стану балки:

а) вантажне: епюра згинаючих моментів М_р будується від заданого навантаження;

   б) одиничне: для визначення прогину у зазначеному перерізі прикладається сила Р = 1; для визначення кута повороту прикладається момент М = 1 (при побудові одиничних епюр 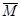 задане навантаження не враховується).

Розбиваємо вантажну епюру згинаючих моментів на прості фігури. Визначаємо площі w_i та вказуємо центр ваги С_i кожної з них.

Знаходимо на одиничній епюрі ординати 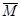, що розташовані під центрами ваги С_i простих фігур вантажної епюри.

Добутки  беруться зі знаком (+) у тому випадку, коли площа w_i і ордината М_i розташовані з однієї сторони від осі (однакові знаки), і зі знаком (-) коли w_i та М_i розташовані по різні сторони від осі (різні знаки) стержня.

Знак (+), отриманий при визначенні переміщень, свідчить про те, що прогин або кут повороту спрямовані у бік одиничного навантаження, знак (-) про те, що переміщення спрямовані убік, протилежний одиничному навантаженню.

4. Розрахунок на жорсткість

Розрахунок на жорсткість полягає в тому, що максимальний прогин у прольоті та на консолі балки не повинен перевищувати заздалегідь заданого розміру, що залежить від довжин прольоту та консоли (який встановлюється нормами проектування).

У прольоті балки:

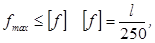                           де  - прольот балки;

      на консолі:

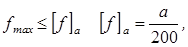                        де а - довжина консоли.

У тому випадку, коли одні або обидві умови не виконуються, робимо підбір балки за умовою жорсткості:

 

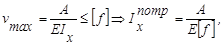
де А - розрахунковий коефіцієнт.

По значенню  за сортаментом прокатних профілів підбирається двотавр.

Переріз з максимальним прогином в прольоті знаходиться там, де кут повороту дорівнює нулю, тобто:

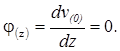
Підставивши знайдене значення z₀ у функцію v_(Z) цієї ділянки, визначаємо v_max.

 

5. Аналіз епюр M_(x), Q_(y), v _(z) і j_(z).

Між функціями M_(z), Q_(z), v_(z) і j_(z) існують відомі залежності:

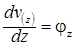                                                                                          (4. 12)

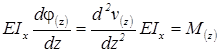                                                                  (4. 13)

                  або                   (4. 14)

 

При побудові епюри кутів повороту j_(z) та прогинів v_(z) повинні спостерігатися згідно співвідношень (4. 12 – 4. 14) такі закономірності:

а) на інтервалі, де згинаючий момент  кут повороту j_(z) зростає, де згинаючий момент 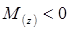 кут повороту j_(z) зменшується; як що при , то функція 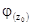 має екстремальне значення; згідно другої формули (4. 14) при  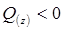епюра j_(z) випинається уверх; в точці при  епюра 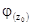 має точку перегину.

б) аналогічну поведінку можна спостерігати між епюрами v_(z), j_(z) та M_(z) згідно формул (4. 12, 4. 13).

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: