 |
4.3. Порядок виконання роботи. 4.4. Зміст роботи. 4.5. Приклад виконання розрахункової роботи № 4
|
|
|
|
4. 3. Порядок виконання роботи
1. Для заданої балки будуємо епюри поперечних сил Q(z) та згинаючих моментів М(z).
2. За умовою міцності за нормальними напруженнями підбираємо розмір двотаврової металевої балки.
3. Виконуємо перевірку міцності балки за sMAX, tMAX та використовуємо одну з теорій міцності.
4. Визначаємо переміщення балки в заданих точках методом початкових параметрів.
5. Визначаємо переміщення у тих же точках балки з використанням засобу Верещагіна (таблиця 4. 1).
6. Результати визначення переміщень заносимо до таблиці 4. 2.
7. Порівнюємо отримані переміщення двома методами, які визначені по розміру і напрямку.
8. Будуємо на одному рисунку епюри  та робимо аналіз цих епюр.
та робимо аналіз цих епюр.
9. Виконуємо розрахунок балки на жорсткість.
4. 4. Зміст роботи
Виконати розрахунок заданої балки на міцність та жорсткість з побудовою відповідних епюр. Проаналізувати отримані результати.
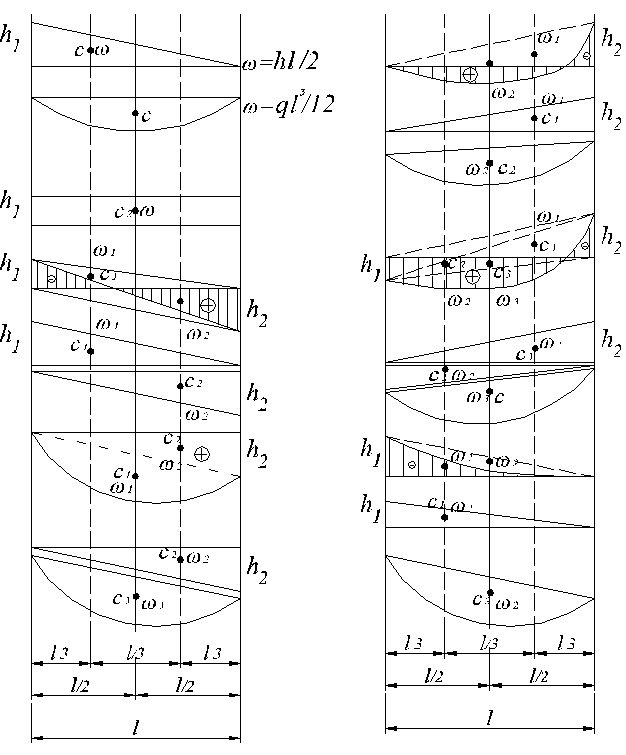 |
Рис. 4. 6
4. 5. Приклад виконання розрахункової роботи № 4
Задано балку, що закріплена і навантажена, як вказано на рис. 4. 7. Р=40 кН, q=20кН/м, М=70кНм, R=210 МПа, Е=2·105 МПа,  = 6м, а=3м.
= 6м, а=3м.
1. Будуємо епюри поперечних сил Q(z) та згинаючих моментів М(z) (рис. 4. 7а, в).
2. За умовою міцності по нормальним напруженням підбираємо поперечний переріз сталевої двотаврової балки:
Мmax =102, 5 кН·м,

За сортаментом приймаємо I № 30: Wx=518 см3, Ix=7780 см4, b=14, 5 см, d=0, 65см, t=1, 07 см, F=49, 9 см2, S 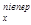 =292см3 (рис. 4. 8).
=292см3 (рис. 4. 8).
Перевірка міцності балки за максимальними нормальними напруженнями:
 Па = 198 МПа < 205 МПа
Па = 198 МПа < 205 МПа
Перевірка міцності балки за максимальними дотичними напруженнями:
|
|
|
Qmax = 70 кН, Rзр = 0, 7R, Rзр = 0, 7·205 = 147 МПа;
 40, 4 МПа < Rзр = 144МПа
40, 4 МПа < Rзр = 144МПа
4. 5. 3. Перевірка балки згідно з IV теорією міцності.
Для аналізованої балки, що задано, перевірку робимо для перерізу mn, який розташовано нескінченно близько справа від точки С (рис. 4. 7):
Mmn = 100кНм, Qmn = 50 кН.
Будуємо епюри sz і ty для небезпечного перерізу двотаврової балки і показуємо напружений стан елементів у точках 1, 2, 3, 4, 5 (рис. 4. 8).
 179 МПа
179 МПа
де  см
см
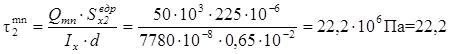 МПа
МПа
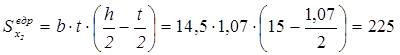 см3.
см3.
 |
Рис. 4. 8
Визначаємо значення еквівалентних напружень за IV теорією міцності:
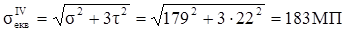 а < R = 210 МПа
а < R = 210 МПа
Умова міцності виконується.
4. 5. 4. Визначаємо прогини та кути повороту методом початкових параметрів у точках А, В, С, D (див. рівняння 4. 9, 4. 10).
Для прикладу, що розглядається (рис. 4. 7) початок координат вибираємо в точці А, де
QА = 0, MА= 0.
Невідомі початкові параметри va і ja знаходимо з умови, що прогини балки в точках В и D дорівнюють 0,
тобто при z = 3 м ® vB = 0 (a)
z = 9 м ® vD = 0 (в)
Умови (а) і (в) підставляємо в рівняння (4. 9)
(а) EІvв = EIva + EIja ·3 - 
або EIva + 3EIja = 67, 5
(b) EIvD = EIva + EIja· 9 + 
або EIva +9EIja = 432, 5 ‚
Розв’язуючи спільно систему рівнянь і ‚
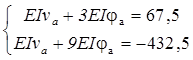 ,
,
одержуємо:
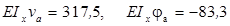 .
.
Визначаємо прогин балки в точці С (z = 7м):

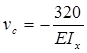
Визначаємо кути повороту в точках B, C, D (z = 3м, z = 7м, z = 9 м відповідно).

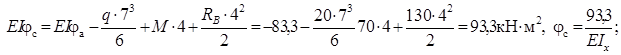

Результати розрахунку заносимо до таблиці 4. 2.
 |
Рис. 4. 7
Таблиця 4. 1
|
|
|
| wi, (кНм2) | EJVА | EJVС | EJjA | EJjB | EJjC | EJjD | ||||||
| Mi, (м) | wiMi | Mi, (м) | wiMi | Mi, (б. р. ) | wiMi | Mi, (б. р. ) | wiMi | Mi, (б. р. ) | wiMi | Mi, (б. р. ) | wiMi | |
| -45 | 1. 5 | -67. 5 | -45 | |||||||||
| -135 | ||||||||||||
| -40 | 
| 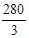
| 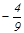
| 
| 
| 
| 
| 
| 
| 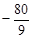
| 
| 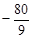
|

| 
| 
| 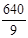
| 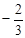
| 
| 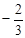
| 
| 
| 
| 
| 
| |
| -200 | 
| 
| 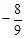
| 
| 
| 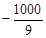
| 
| 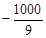
| 
| 
| 
| 
|
| -100 | 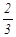
| 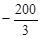
| 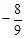
| 
| 
| 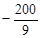
| 
| 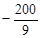
| 
| 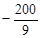
| 
| 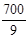
|
| SwiMi | -317 | -83. 3 | -173. 3 | 93. 3 | 193. 3 | |||||||
4. 5. 5. Визначаємо прогини та кути повороту в точках A, B, C, D засобом Верещагіна.
Розглядаємо два стани балки: вантажне (епюру Мр від заданого навантаження “а”) та одиничне - у точках А і С, де необхідно визначити прогини послідовно прикладаємо одиничну силу Р = 1 і будуємо відповідні епюри моментів 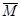 “b” і “с” (рис. 4. 8)
“b” і “с” (рис. 4. 8)
У точках A, B, C, D, де необхідно визначити кути повороту, послідовно прикладаємо одиничні моменти M = 1 і будуємо відповідні епюри моментів 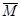 “d”, “e”, “f”, “g” (рис. 4. 8).
“d”, “e”, “f”, “g” (рис. 4. 8).
Вантажну епюру відповідно до рекомендацій (рис. 4. 6) розбиваємо на шість простих фігур, що мають відповідно площі w1, , w2, , w3, , w4, , w5, і w6 (рис. 4. 8):

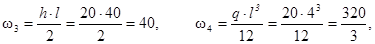

Подальші обчислення робимо в табличному вигляді (табл. 4. 1).
У перший стовбчик заносимо значення площ wj (j=1, 2, 3, 4, 5, 6).
Потім для кожного одиничного стана обчисляємо відповідно до рекомендацій (рис. 4. 6) значення ординат Мі.
Значення переміщень, помножених на EI, подані в нижньому рядку таблиці 4. 1.
Результати обчислень заносимо до таблиці 4. 2 та відповідно до їх знаків визначаємо напрямок переміщень.
4. 5. 7. Порівнюємо за величиною та напрямком переміщення в заданих точках, що знайдені двома методами. З таблиці 4. 2 випливає, що напрямки та величини переміщень, визначені відповідними правилами знаків збігаються. Визначаємо чисельні значення прогинів і кутів повороту в заданих точках:


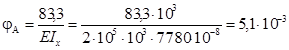 рад.
рад.
 рад.
рад.
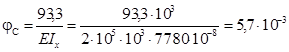 рад.
рад.
 рад.
рад.
Таблиця 4. 2
|
|
Метод П. П. | Спосіб Верещагина | Величина переміщения | |||
| величина | напрямок | величина | напрямок | vZ, (см) | jZ (рад) | |
 va va
| 
| 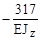
| 1. 94 | - | ||
| vc | 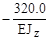
| 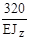
| 1. 96 | - | ||
| ja | 
| 
| - | 
| ||
| jв | 
| 
| - | 
| ||
| jс | 
| 
| - | 
| ||
| jD | 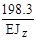
| 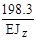
| - | 
| ||
|
|
|
4. 5. 8. Будуємо на однім рисунку епюри  і аналізуємо їх відповідно до приведених раніше залежностей (4. 12 - 4. 14), рис. 4. 7.
і аналізуємо їх відповідно до приведених раніше залежностей (4. 12 - 4. 14), рис. 4. 7.
4. 5. 9. Розрахунок балки на жорсткість.
Прольот балки BD, 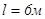 , прогин, що припускається
, прогин, що припускається 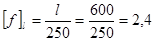 см.
см.
Визначаємо vmax у прольоті балки.
Аналітичне рівняння пружньої лінії представляємо за методом початкових параметрів
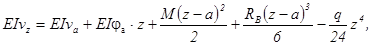

Після спрощення
33, 3z03 -65z02 +320z0 -292 = 0.
Звідси z0 = 6, 07 м.
Максимальний прогин дорівнює:
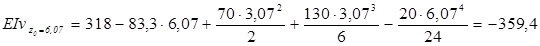 к× Нм3
к× Нм3
 см < [ f ] = 2, 4 см.
см < [ f ] = 2, 4 см.
Балка в прольоті задовольняє умові жорсткості.
Консоль балки АВ, а =3м: де прогин, що допускається  см.
см.
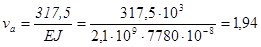 см
см
Тому що va = 1, 94 см > [f]а = 1 см, балка на консолі не задовільняє умові жорсткості. Тому розмір двотавра підбираємо з умови жорсткості. Для цього визначаємо потрібний момент інерції:
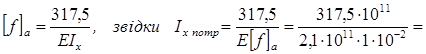 15120см4
15120см4
Остаточно приймаємо балку з I № 40, Ix=19062 см4 > 15120 см4, тобто за умовою жорсткості на консолі.
Рис. 4. 9
 |
|
|
|


