 |
розрахунково-проектувальна робота 5
|
|
|
|
розрахунково-проектувальна робота 5
Розрахунок бруса на складний опір
5. 1. Питання до самостійної роботи
1. Коли виникає складний опір бруса? Які види складного опору ви знаєте?
2. Сформулюйте умови, при яких виникає косий згин.
3. Сформулюйте правило знаків для згинаючих моментів. Що означають індекси в позначеннях згинаючих моментів?
4. Що таке силова лінія? Як визначається її положення при косому згині?
5. Що таке нейтральна лінія? Запишіть формулу за якою визначається положення цієї лінії при косому згині.
6. Для яких форм поперечних перерізів балок можна сказати, що в них косий згин не виникає?
7. Як визначається положення небезпечного перерізу в балці при косому згині? Яка залежність при цьому застосовується?
8. Запишіть умову міцності балки при косому згині. Поясніть зміст цієї формули. Які типи задач міцності можна вирішувати з її допомогою?
9. Поясніть зміст формули нормальних напружень для довільної точки поперечного перерізу балки при косому згині. Порівняйте її з формулою нормальних напружень при плоскому чистому згині.
10. Зазначте на відмінність епюр нормальних напружень при косому і площинному згині.
11. Продумайте питання про те, як будуть проходити нейтральна і силова лінії при різноманітних знаках згинаючих моментів.
12. Сформулюйте умови, при яких виникає позацентровий розтяг (стиск).
13. Які внутрішні зусилля виникають при позацентровому розтягу (стиску)?
14. Як визначаються нормальні напруження при позацентровому розтягу (стиску)?
15. Що таке нейтральна лінія? Яким чином визначається її положення? Як проходить силова лінія при позацентровому розтягу (стиску)?
|
|
|
16. Яким чином залежить положення нейтральної лінії від розташування точки завантаження короткого стояка?
17. Що називається ядром перерізу поперечного переріза?
18. Як будується ядро перерізу для прямокутника, кола, двотавра, швелера?
19. Чому дорівнюють нормальні напруження в центрі ваги перерізу при позацентровому стиску? Чи залежать їх значення від зміни положення точки навантаження?
20. Де лежить точка навантаження сили у випадку, коли нейтральна лінія дотикається контуру поперечного перерізу короткого стояка?
21. Чому при побудові ядра перерізу треба задаватися положенням нейтральної лінії, що дотикається контуру поперечного перерізу стояка?
22. Пригадайте умову міцності при позацентровому стиску короткого стояка, матеріал якого має різноманітні характеристики на міцність при розтягу і стиску.
5. 2. Стислі теоретичні зведення
5. 2. 1. Розрахунок балки на складний (косий згин)
При розрахунку балки на міцність при складному згині будують епюри згинаючих моментів у головних площинах інерції, що у наших задачах збігаються з горизонтальною і вертикальною площинами.
Правило знаків для згинаючих моментів:
згинаючі моменти Мx(z) або Му(z) приймаються позитивними, якщо вони викликають розтяг поздовжніх волокон, що належать першій координатній чверті головних центральних осей інерції х, у поперечного перерізу балки.
 |
Це правило необхідно для правильного запису рівнянь згинаючих моментів і пов'язаних із ними нормальних напружень. Позитивні напрямки моментів показано на рис. 5. 1
Рис. 5. 1
Нормальні напруження в довільній точці А (х, у) поперечного перерізу балки при складному і косому згині (рис. 5. 1).
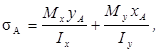(5. 1)
де Ix, Iу - значення головних осьових моментів інерції.
|
|
|
Враховуючи те, що головні моменти опору поперечного переізу балки на згин
,
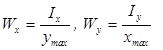нормальні напруження в найбільш віддалених волокнах прямокутного поперечного перерізу можуть бути знайдені за формулою:
(5. 2)
Знаки у формулі (5. 2) приймають по знаках координат x, y та згинаючих моментів Мx і Мy формули (5. 1).
Умова міцності балки, матеріал якого однаково чинить опір розтягу та стиску має вигляд:
, (5. 3)
де R - розрахунковий опір матеріалу балки.
Раціональне розташування прямокутного перерізу балки визначається величинию більшого за модулем згинаючого момента у вертикальній і горизонтальній площинах.
Якщо згинаючий момент |Мх| > |Му|, переріз балки потрібно розташувати так, щоб момент опору Wx був більше Wy.
Подумайте, чому так?
Для прямокутного перерізу маємо (рис. 5. 1):
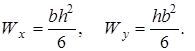
5. 2. 2. Розрахунок короткої стійки при позацентровому стиску
Позацентровий стиск (розтяг) виникає тоді, що коли рівнодіюча зовнішніх сил Р спрямована паралельно поздовжній осі бруса, а точка В її прикладання розташована щодо центру ваги з деяким ексцентриситетом e із компонентами хр, ур по напрямку головних центральних осей х, у, відповідно (рис. 5. 2). Приводячи силу Р в центр ваги перерізу, можна одержати статично еквівалентне навантаження: поздовжня сила N=-P і дві пари сил із моментами Му=-Р·xр та Мх=-Р·yр, що викликають відповідно центральний стиск і чистий згин у головних площинах інерції zoy і zox (рис. 5. 3). Знак (-) вказує на те, що всі зазначені тут зусилля стискують поздовжнє волокно стійки в першій чверті головних осей інерції xoy.
 |
Нормальні напруження в довільній точці А(х, у) переріза можна знайти за формулою
(5. 4)
З урахуванням співвідношень
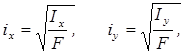(5. 5)
що означають величини значення головних радіусів інерції перерізу, отримаємо:
(5. 4*)
На відміну від складного (косого) згину при позацентровому стиску нейтральна лінія не проходить через центр ваги перерізу. Положення цієї лінії, з умови рівності нулю нормальних напружень s, визначимо відрізками, які вона відсікає на головних осях інерції:
|
|
|
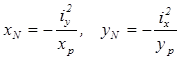(5. 6)
Нейтральна лінія поділяє площу перерізу на дві частини, у яких нормальні напруження s мають протилежні знаки. Положення нейтральної лінії залежить від координат точки В, де прикладена сила Р. Найбільші за модулем величини нормальних напружень виникають у найбільш віддалених точках у стиснутій та розтягнутій зонах перерізу. Для визначення положення цих точок достатньо провести дотичні до контуру перерізу, паралельні нейтральній лінії. Точки дотику і будуть точками з найбільшими за модулем нормальними напруженнями. Важливо відзначити такі положення: якщо точка прикладання сили лежить на однієї з головних осей інерції і переміщається уздовж неї, то нейтральна лінія також переміщається, залишаючись паралелльною іншій головній осі інерції. Справедливо й обернене затвердження: якщо нейтральна лінія переміщується, залишаючись паралельно однієї з головних осей інерції, то точка прикладання В сили Р переміщується уздовж іншої головної осі інерції (рис. 5. 4). Варто зауважити, якщо сила наближується до центру ваги перерізу, нейтральна лінія віддаляється в безкрайність.
 |
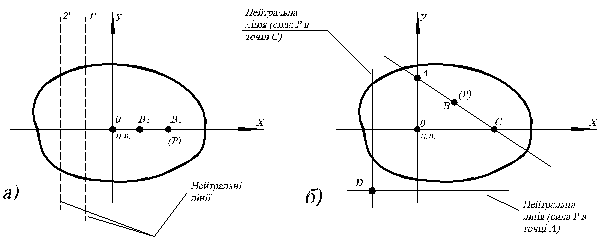Рис. 5. 4
З рис. 5. 4 б випливає, якщо точка В прикладання сили Р переміщується уздовж прямої АС загального положення (із точки В до точки С), то нейтральна лінія повертається навколо деякої точки D. Справедливе й обернене затвердження: якщо нейтральну лінію повертати навколо деякої точки D, то точка прикладання сили буде переміщуватися уздовж прямої АС загального положення. Обернені затвердження широко використовуються при побудові деякої уявлюваної області, розташованої навколо центру ваги. Ця область має чудову властивість: у якій би точці цієї області не знаходилася сила Р, у всіх точках поперечного перерізу нормальні напруження s матимуть один знак. Цю область прийнято називати ядром перерізу.
Очевидно, якщо сила буде знаходитись на контурі ядра перерізу, нейтральна лінія буде дотичною до контура поперечного перерізу. Звідси випливає правило побудови ядра перерізу. Задаємося серією нейтральних ліній, дотичних до контура поперечного перерізу, визначаємо для кожної із них відрізки, що відсікаються на головних осях інерції ах і ау відповідно, (з урахуванням знаків), та за формулами:
|
|
|
(5. 7)
знайдемо координати точок, що належать контуру ядра перерізу. Розміри відрізків ах та ау для перерізу ломаного обрису можна знайти з рівняння прямої, що проходить через дві точки:
(5. 8)
де x1, y1 і x2, y2 - координати точок контуру перерізу, через які проходить задана нейтральна лінія;
x, y - поточні координати точок нейтральної лінії.
Якщо прийняти y = 0, x = ах, то
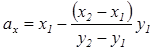(5. 9)
А якщо прийняти x = 0, y = ау, то
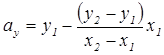(5. 10)
Якщо обрис контуру перерізу криволінійний, то необхідно написати рівняння лінії цього контуру. Потім записати рівняння дотичної до цієї лінії і визначити відповідні відрізки, що відсікаються нейтральною лінією на головних осях інерції. У роботі це не використовується, тому такі співвідношення тут не приводяться.
|
|
|
